Содержание
- 2. ? 1.1. Площадь плоской фигуры
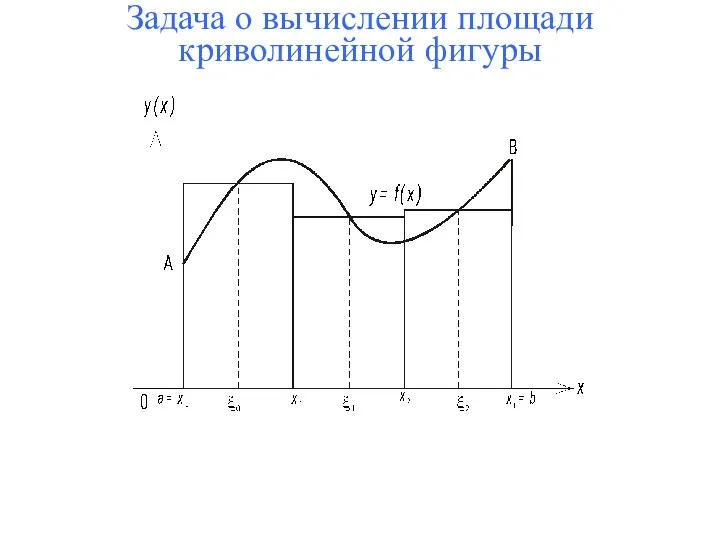
- 3. Задача о вычислении площади криволинейной фигуры
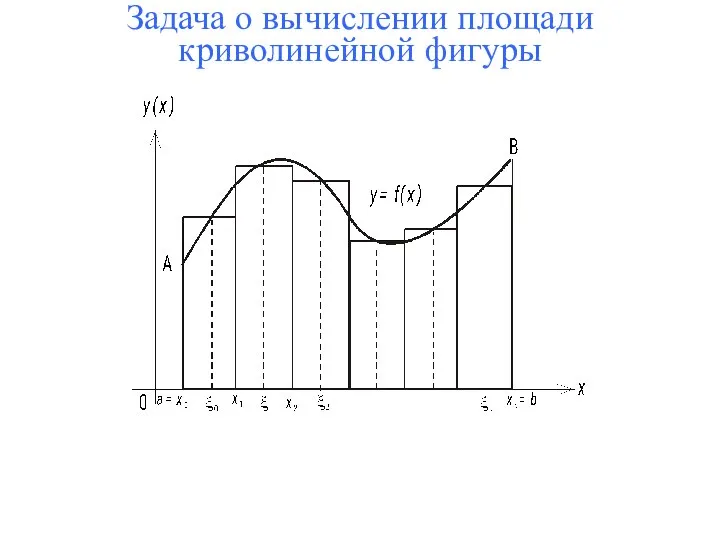
- 4. Задача о вычислении площади криволинейной фигуры
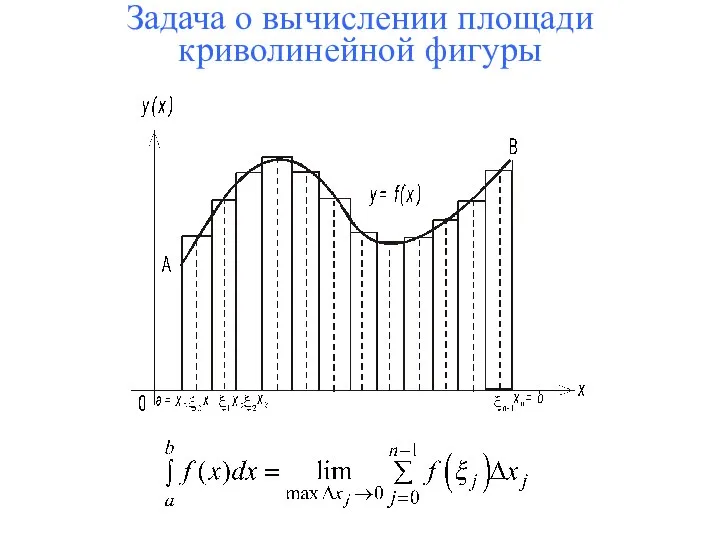
- 5. Задача о вычислении площади криволинейной фигуры
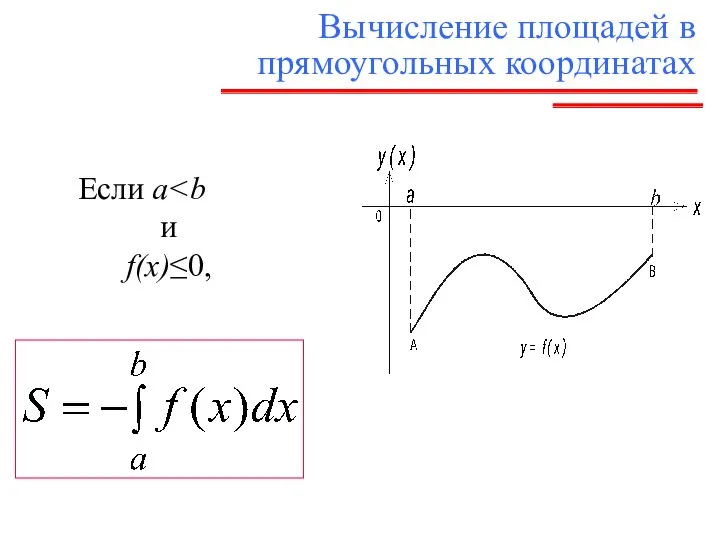
- 6. Вычисление площадей в прямоугольных координатах Если a и f(x)≥0,
- 7. Вычисление площадей в прямоугольных координатах Если a и f(x)≤0,
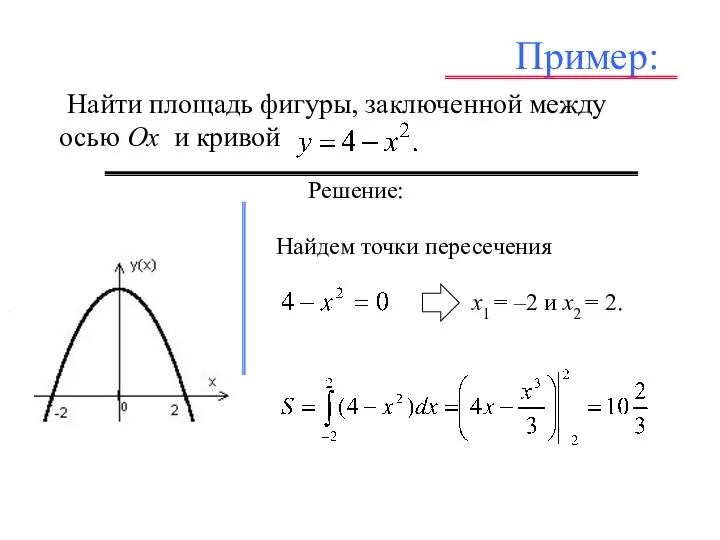
- 8. Пример: Найти площадь фигуры, заключенной между осью Ох и кривой – . .
- 9. Пример: Найти площадь фигуры, заключенной между осью Ох и кривой – . Решение: . Найдем точки
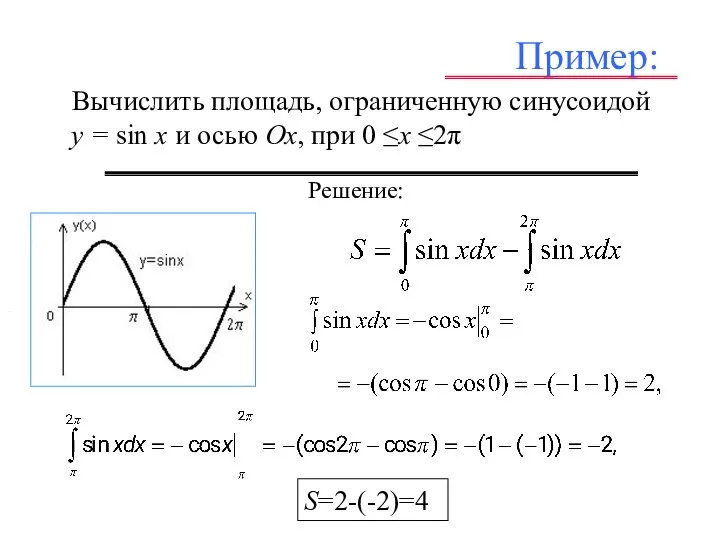
- 10. Пример: Вычислить площадь, ограниченную синусоидой y = sin x и осью Ox, при 0 ≤х ≤2π
- 11. Пример: Вычислить площадь, ограниченную синусоидой y = sin x и осью Ox, при 0 ≤х ≤2π
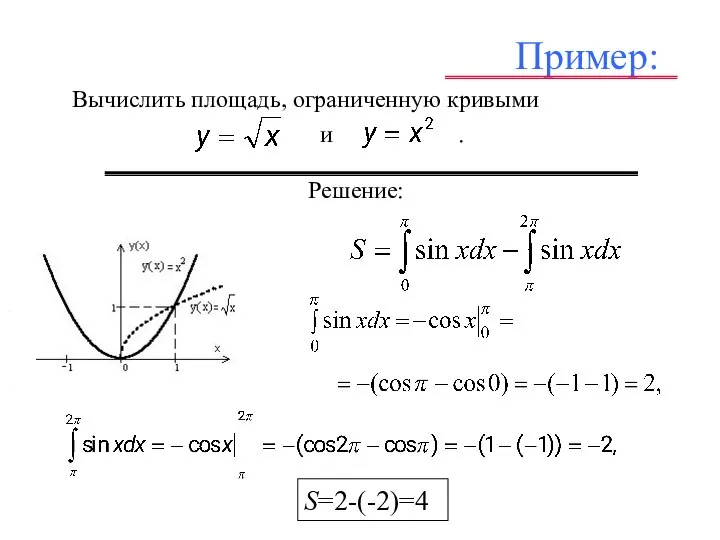
- 12. Вычислить площадь, ограниченную кривыми и . Пример: – . .
- 13. Пример: Вычислить площадь, ограниченную кривыми и . – . Решение: . S=2-(-2)=4
- 14. Вычисление площадей кривых, заданных параметрически Если кривая задана параметрическими уравнениями х = x(t), y = y(t),
- 15. Замечание Формула применима также для вычисления площади фигуры, ограниченной замкнутой кривой (изменение параметра t от t1
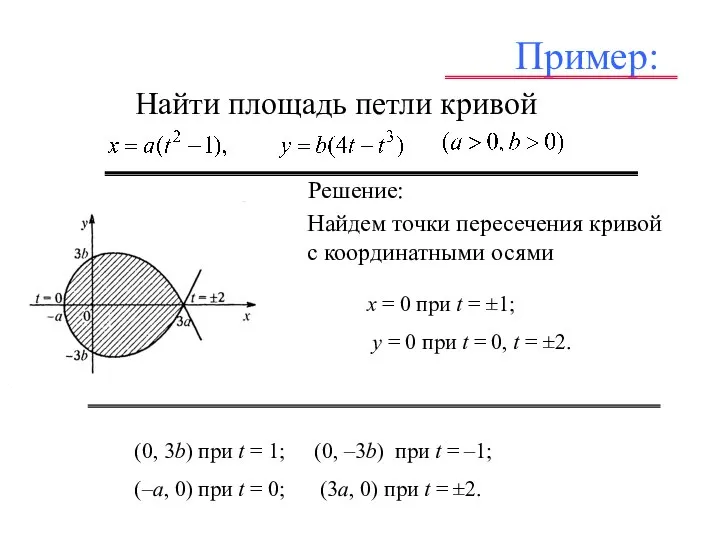
- 16. Пример: – . . Найти площадь петли кривой
- 17. Пример: Найти площадь петли кривой – . Решение: . Найдем точки пересечения кривой с координатными осями
- 18. Пример: Найти площадь петли кривой . Решение: (0, 3b) при t = 1; (0, –3b) при
- 19. Вычисление площадей в полярных координатах Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением ρ
- 20. Пример: Вычислить площадь лунки, ограниченной дугами окружностей . , , .
- 21. Пример: Вычислить площадь лунки, ограниченной дугами окружностей . Решение: , , . Окружности пресекаются при .
- 22. ? 1.2. Длина дуги кривой
- 23. В декартовых координатах: Если гладкая кривая задана уравнением y = f(x), то длина l ее дуги:
- 24. Пример: Найти длину полукубической параболы от начала координат до точки (4, 8). . , , .
- 25. Пример: Найти длину полукубической параболы от начала координат до точки (4, 8). . , , .
- 26. Кривая задана параметрически : x = x(t), y = y(t), (t1 ≤ t ≤ t2):
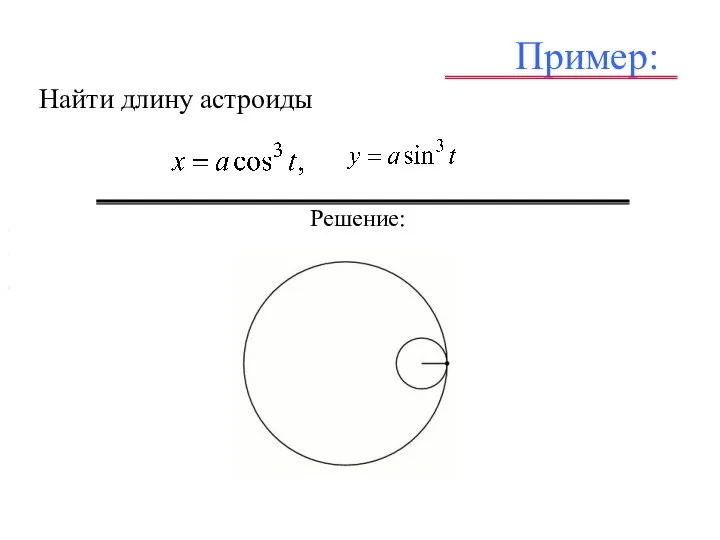
- 27. Пример: Найти длину астроиды . , , . Решение: , , ,
- 28. Пример: Найти длину астроиды . , , . Решение: , , , , ,
- 29. Кривая задана параметрически : x = x(t), y = y(t), z = z(t), (t1 ≤ t
- 30. В полярных координатах Если задано полярное уравнение гладкой кривой ρ = ρ (ϕ) и двумя лучами
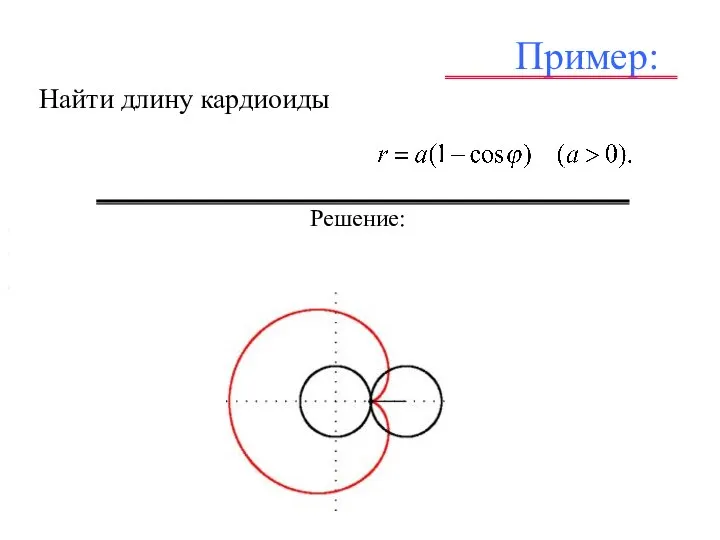
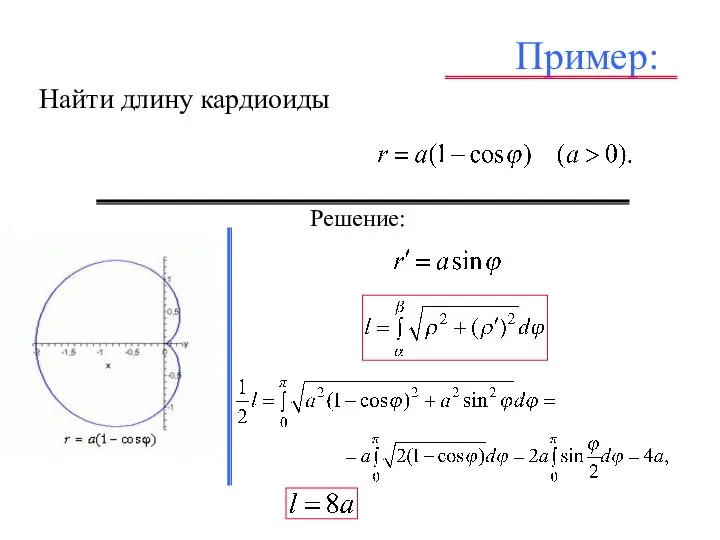
- 31. Пример: Найти длину кардиоиды . , , . Решение: , , ,
- 32. Пример: Найти длину кардиоиды . , , . Решение: , , ,
- 33. ? 1.3 Объем тела
- 34. Объем тела по площадям его параллельных сечений Если площадь S(x) сечения тела плоскостью, перпендикулярной оси Ох,
- 35. Пример: Найти объем тела, основание которого – круг радиуса а, а сечение плоскостью, перпендикулярной фиксированному диаметру
- 36. Объем тела вращения Если криволинейная трапеция ограничена графиком непрерывной функции и прямыми то объем тела, образованного
- 37. Объем тела вращения
- 38. Пример: Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями . , , .
- 39. Объем тела вращения Если криволинейный сектор, ограниченный кривой и лучами вращается вокруг полярной оси, то объем
- 40. Пример: , , . Решение: , , , Кардиоида вращается вокруг полярной оси. Найти объем тела
- 41. Площадь поверхности вращения Если криволинейная трапеция ограничена графиком непрерывной функции и прямыми то площадь поверхности вращения,
- 42. Площадь поверхности вращения Если кривая задана параметрическими уравнениями , Если дуга задана в полярных координатах
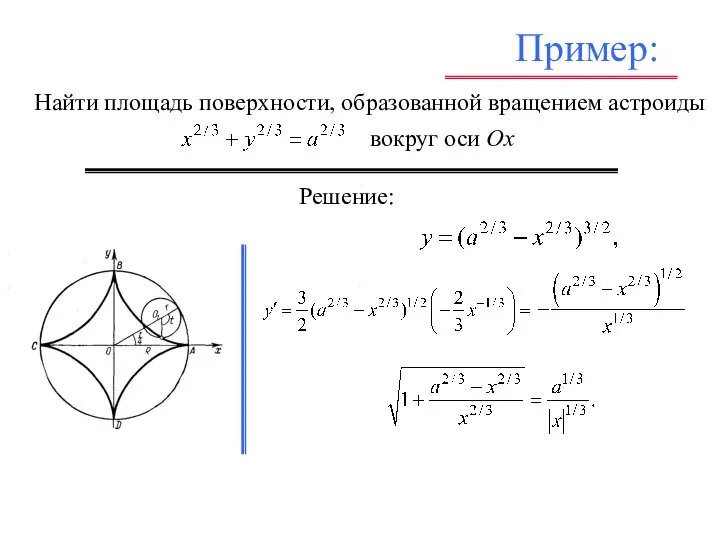
- 43. Пример: , , . Решение: , , , Найти площадь поверхности, образованной вращением астроиды вокруг оси
- 44. Пример: , , . , , ,
- 45. ? 2 Механическое приложение
- 46. Пройденный путь Путь, пройденный точкой за промежуток времени [t0, T], равен соответствующему определенному интегралу от скорости
- 47. Работа Работа, произведенная силой F при перемещении точки М из положения s=a в положение s=b, равна
- 48. Масса стержня переменной плотности Будем считать, что отрезок [a ,b] оси х имеет массу с переменной
- 49. ? 3 Приближенное вычисление
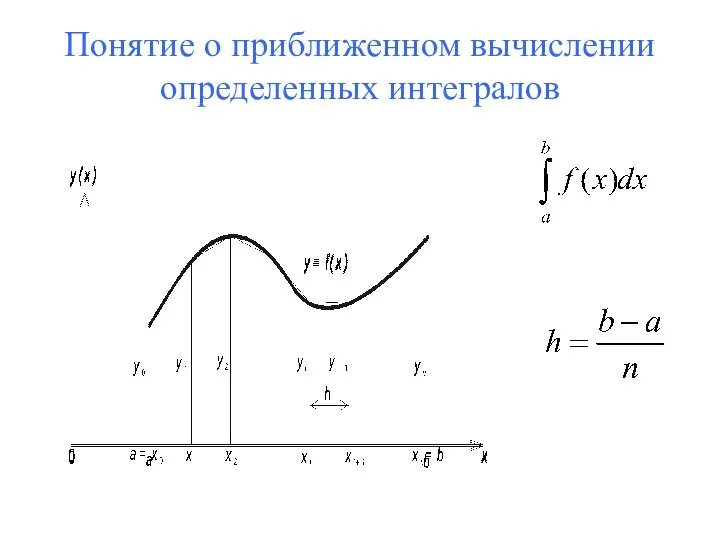
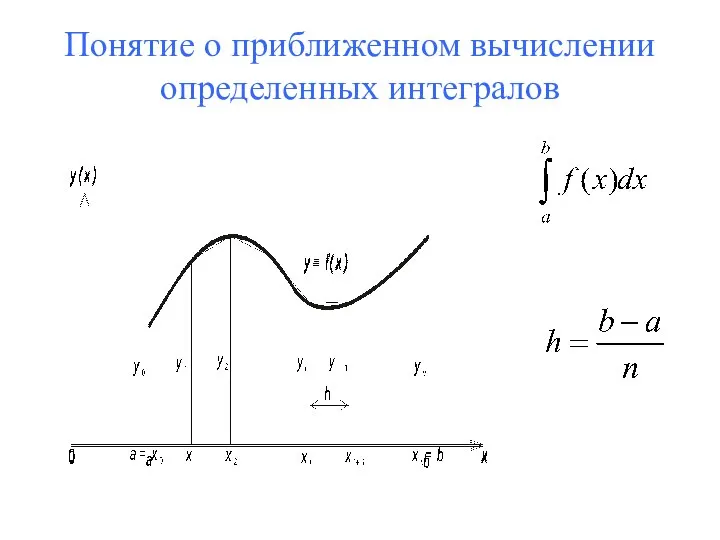
- 50. Понятие о приближенном вычислении определенных интегралов
- 51. Понятие о приближенном вычислении определенных интегралов
- 53. h=0,1
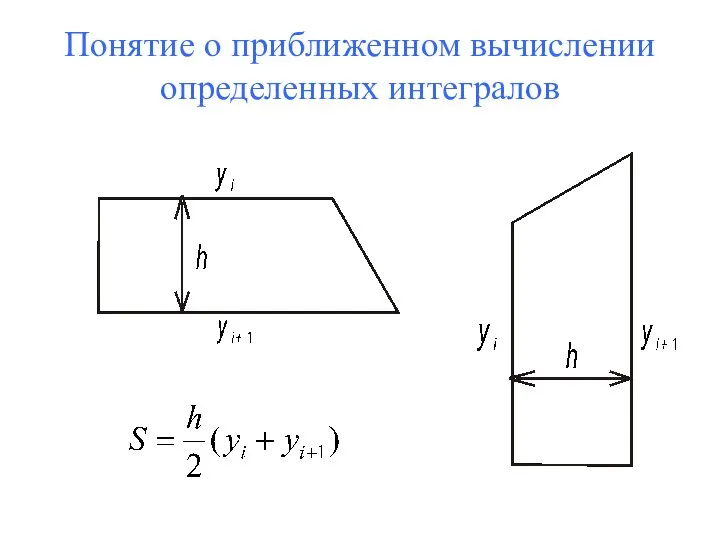
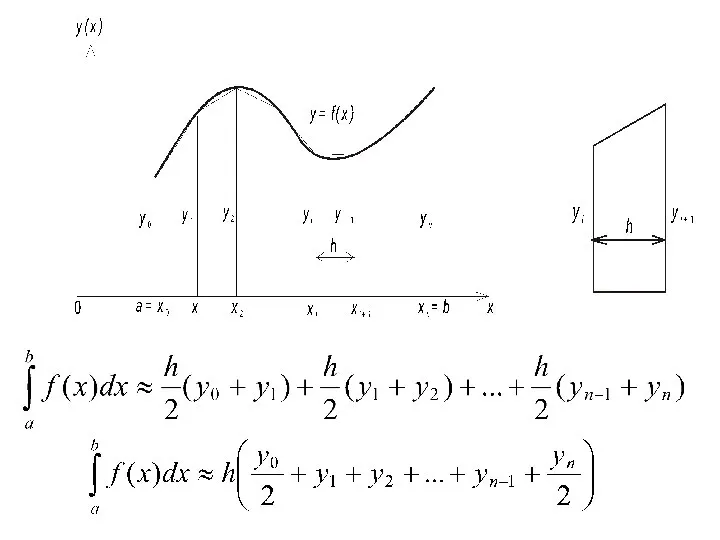
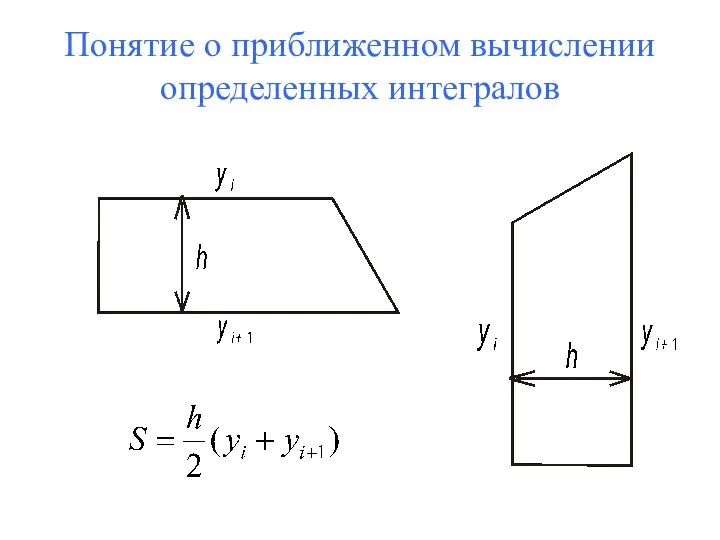
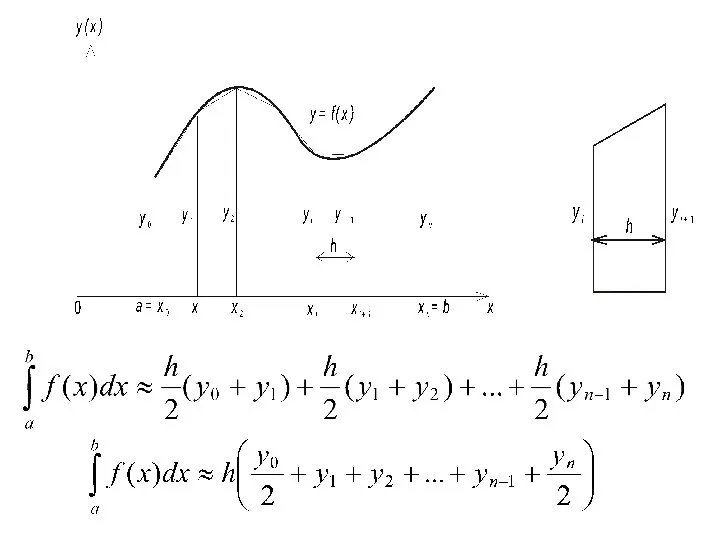
- 55. Понятие о приближенном вычислении определенных интегралов
- 56. Понятие о приближенном вычислении определенных интегралов
- 58. h=0,1
- 60. Спасибо за внимание!
- 62. Скачать презентацию
































![Пройденный путь Путь, пройденный точкой за промежуток времени [t0, T], равен](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1302419/slide-45.jpg)

![Масса стержня переменной плотности Будем считать, что отрезок [a ,b] оси](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1302419/slide-47.jpg)


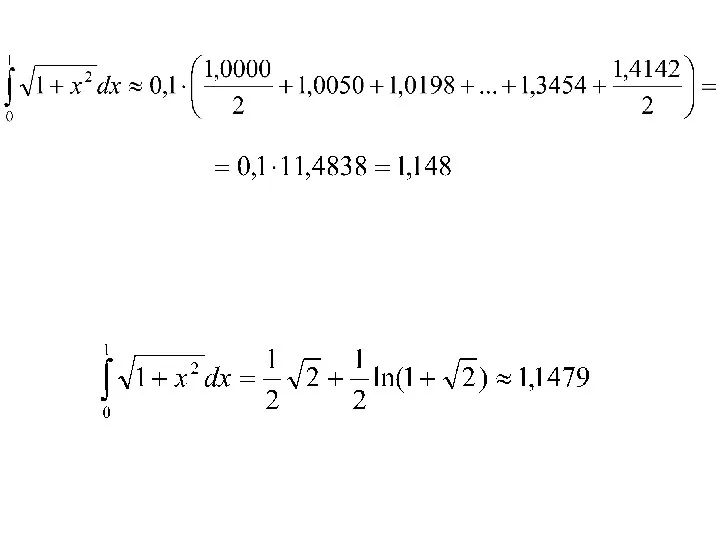

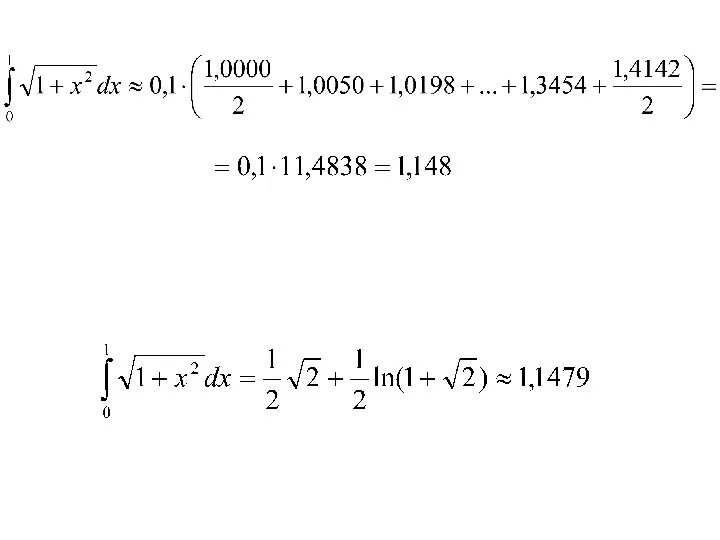

 Консерваторы в конце 50-ых и в начале 60-ых гг.
Консерваторы в конце 50-ых и в начале 60-ых гг. Идеал семейной жизни в житиях русских святых
Идеал семейной жизни в житиях русских святых Программирование на языке Java. Примитивные типы данных. Операции, комментарии. (Лекция 2.1)
Программирование на языке Java. Примитивные типы данных. Операции, комментарии. (Лекция 2.1) Застольный этикет
Застольный этикет Istoria_razvitia_nevrologii
Istoria_razvitia_nevrologii Перфоманс, хэппенинг, инсталляция
Перфоманс, хэппенинг, инсталляция Конституційно-правова відповідальність
Конституційно-правова відповідальність Ленинградская фонетическая школа
Ленинградская фонетическая школа Усиление каменных конструкций. Часть 1
Усиление каменных конструкций. Часть 1 Заболевания сосудов
Заболевания сосудов Управление в сфере антимонопольного и тарифного регулирования
Управление в сфере антимонопольного и тарифного регулирования lection_3_IDO.ppt
lection_3_IDO.ppt Понятие архитектуры ЭВМ и общие механизмы функционирования
Понятие архитектуры ЭВМ и общие механизмы функционирования Принципы организации Прокуратуры Российской Федерации
Принципы организации Прокуратуры Российской Федерации Усеченный инфинитив
Усеченный инфинитив Châteaux de la Loire
Châteaux de la Loire K-P-T vaihtelu Nominityypit Vartalot Harjoitukset (1)
K-P-T vaihtelu Nominityypit Vartalot Harjoitukset (1) Иммунопрофилактика
Иммунопрофилактика Классификация видов искусства
Классификация видов искусства О схемах программ Схема проектирования цикла с помощью инварианта
О схемах программ Схема проектирования цикла с помощью инварианта Экологическая игра « Поле чудес» - презентация для начальной школы_
Экологическая игра « Поле чудес» - презентация для начальной школы_ Lin/ltl 487 second language pedagogy. Week 8
Lin/ltl 487 second language pedagogy. Week 8 Массивы
Массивы Принадлежность точки линии
Принадлежность точки линии Развитие новых технологий XVII-XXI века
Развитие новых технологий XVII-XXI века это вид искусства, в котором художественные образы создаются средствами пластических движений и ритмически четкой и непрерывной
это вид искусства, в котором художественные образы создаются средствами пластических движений и ритмически четкой и непрерывной  Рождество (Christmas). Что такое Рождество?
Рождество (Christmas). Что такое Рождество? ГБ4лечение для ВОГ
ГБ4лечение для ВОГ