Содержание
- 2. Агнер Краруп Эрланг 1878-1929гг., родился в Дании Пришел в Копенгагенскую Телефонную Компанию в 1908 году как
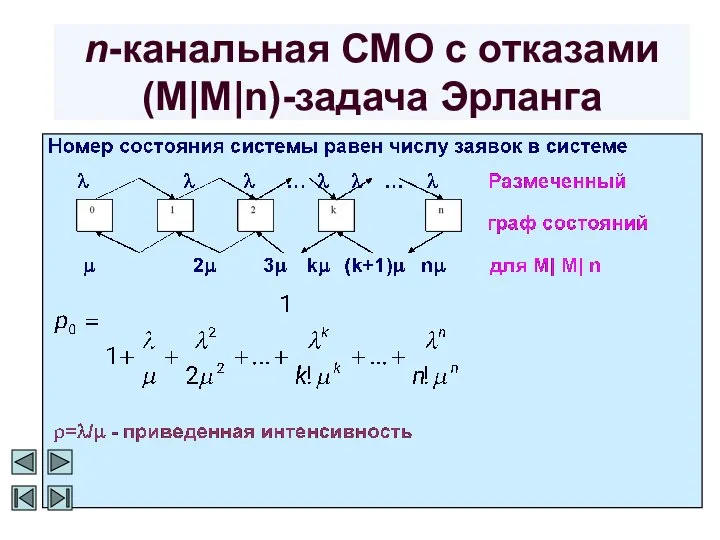
- 3. Простейшие СМО n-канальная СМО с отказами (M|M|n) - задача Эрланга
- 4. n-канальная СМО с отказами (M|M|n)-задача Эрланга
- 5. Показатели эффективности
- 6. Показатели эффективности
- 7. Пропускная способность Q=1-Ротк – относительная A=λQ – абсолютная Показатели эффективности
- 8. k= 0 1 2 3 … n p0 p1 p2 p3 … pn kср = 0
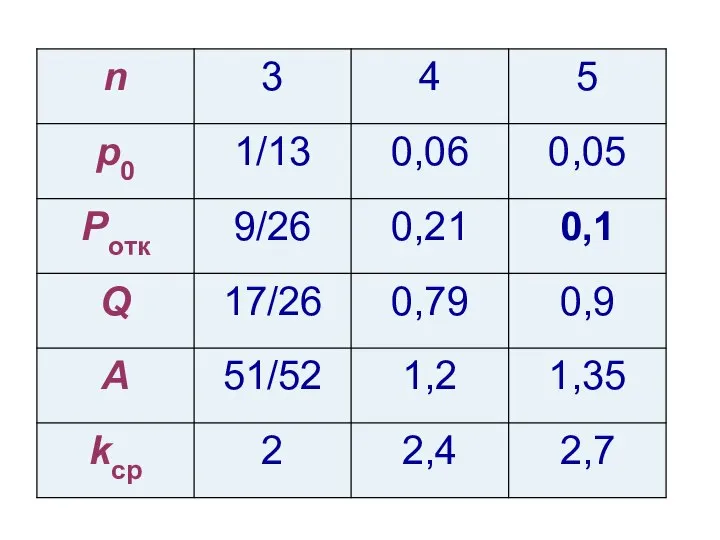
- 9. M|M|n - задача Эрланга Пример Станция связи с тремя каналами (n=3), интенсивность потока заявок λ= 1,5
- 10. Пример 1. Имеется станция связи с тремя каналами (n=3), интенсивность входного потока λ= 1,5 заявки в
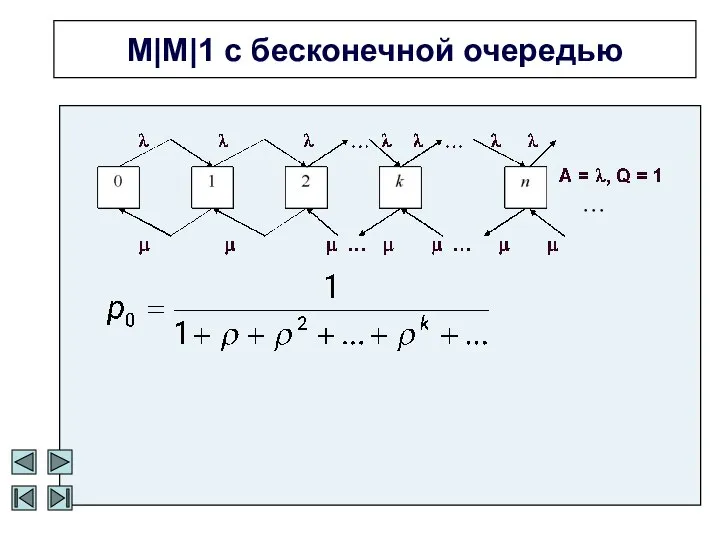
- 13. М|М|1 с бесконечной очередью …
- 14. p0=1-ρ … Как бы ни была нагружена система с очередью, если только она вообще справляется с
- 15. Одноканальная СМО с неограниченной очередью Найдем среднее число заявок в СМО Lсист . Случайная величина Z
- 16. Рзан=1-pо=ρ
- 17. Пример Одноканальная СМО - железнодорожная сортировочная станция, на которую поступает простейший поток составов с интенсивностью λ=2
- 18. Найти (для стац. режима работы станции): среднее число составов Lсист, связанных со станцией, среднее время Wсист
- 19. Решение Интенсивность обслуживания μ=3 (состава/час), ρ=2/3, Тогда - Lсист=2 - Lоч=4/3 (состава) Соответственно, по формулам Литтла
- 20. Многоканальная СМО с неограниченной очередью Номер состояния системы равен числу заявок в системе: S0 − в
- 21. ρ/п p1=ρp0, …,
- 22. Характеристики эффективности Абсолютная пропускная способность СМО А равна среднему числу заявок, поступающих в систему в единицу
- 23. Пример Железнодорожная касса по продаже билетов с двумя окошками - двухканальная СМО с неограниченной очередью, устанавливающейся
- 25. Одноканальная СМО с ограниченной очередью число заявок в очереди ограничено (не может превосходить некоторого заданного m
- 26. Вер{канал занят}=1-Вер{канал свободен}=1− p0. Pотк=Вер{заняты все места в очереди}=pm+1= Тогда относительная пропускная способность Q=1-Pотк= Абсолютная пропускная
- 27. Пример 2. Банк принимает решение об открытии филиала, рассматривая его как многоканальную систему с отказами. Входной
- 28. Решение. В стационарном режиме средний доход, приносимый СМО за время τ, D(τ) =АС1τ, где А −
- 29. D(τ)=Сср(τ) время, после которого СМО будет приносить прибыль,
- 30. Пример 3. При строительстве контакт-центра необходимо оптимизировать количество операторских мест. Для этого нужно знать среднюю продолжительность
- 31. Пусть средняя продолжительность разговора равна 160 с, количество звонков – 240 в час, время поствызывной обработки
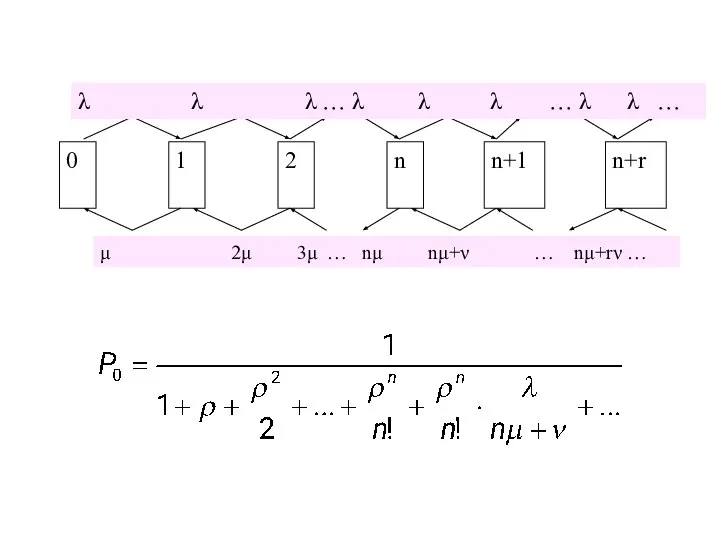
- 32. СМО с ограниченным временем ожидания M/M/n, очередь бесконечна, но время пребывания заявки в очереди ≤ Точ
- 33. μ 2μ 3μ … nμ nμ+ν … nμ+rν … λ λ λ … λ λ λ
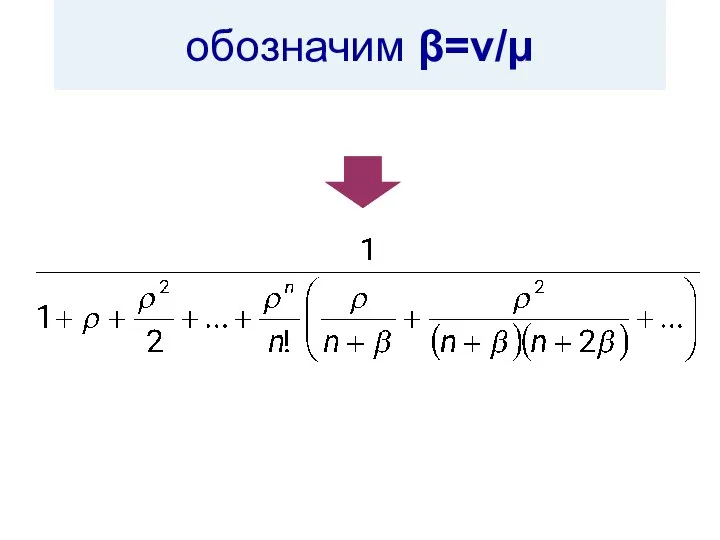
- 34. обозначим β=ν/μ
- 35. Замкнутые системы массового обслуживания Рабочий-наладчик обслуживает n станков. Каждый станок может с интенсивностью λ в любой
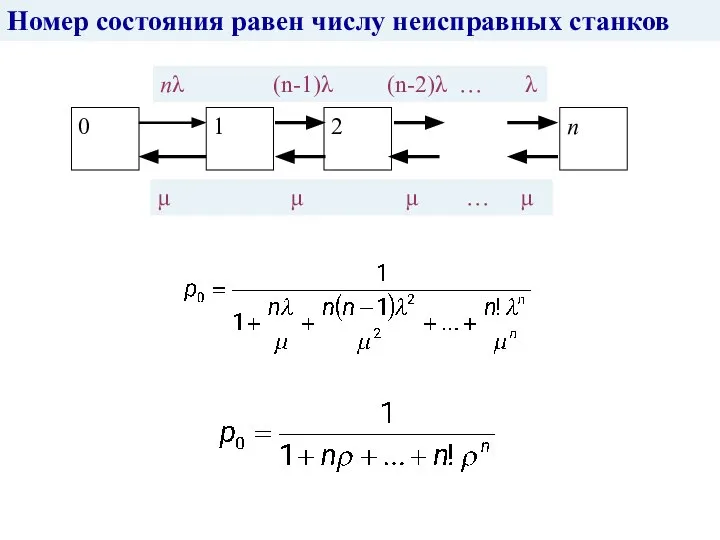
- 36. nλ (n-1)λ (n-2)λ … λ μ μ μ … μ Номер состояния равен числу неисправных станков
- 37. Абсолютная пропускная способность А – это “среднее количество заявок, прошедших через систему в единицу времени”, в
- 38. Относительная пропускная способность Q=1, т.к. каждая заявка в конце концов будет обслужена. Среднее число неисправных станков
- 39. Среднее число заявок в системе Lсист=ϖ. Среднее число заявок в очереди Lоч=Lсист -Mν, где ν -
- 40. Пример Рабочий обслуживает группу из трех станков. Каждый станок останавливается в среднем 2 раза в час.
- 41. Немарковские СМО n-канальная СМО с отказами, с простейшим потоком заявок и произвольным распределением времени обслуживания -
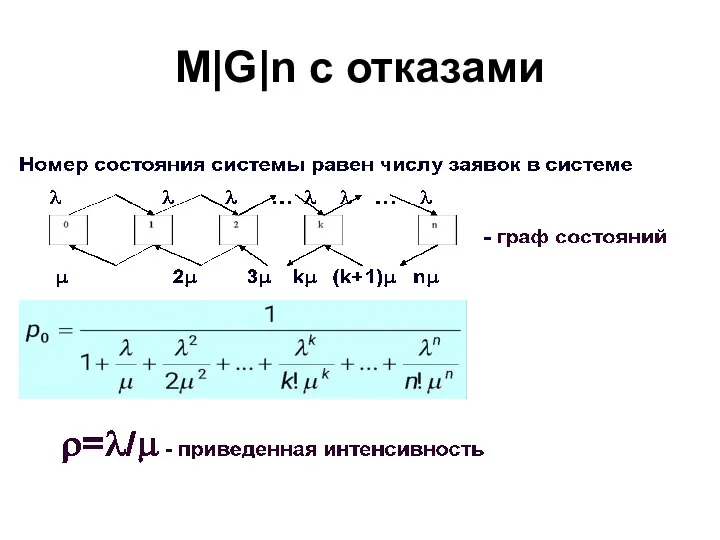
- 42. M|G|n с отказами
- 43. M|G|n с отказами Формулы Эрланга
- 44. Показатели эффективности Пропускная способность Q=1-Ротк – относительная A=λQ – абсолютная kср=A/μ - среднее число занятых каналов
- 45. Немарковские СМО Одноканальная СМО с неограниченной очередью, простейшим потоком заявок и произвольным распределением времени обслуживания M|
- 46. M| G| 1 с бесконечной очередью Время обслуживания распределено по произвольному закону с мат. ожиданием tμ
- 47. Формулы Поллачека-Хинчина
- 48. M|M|1 Время обслуживания распределено по экспоненциальному закону с мат. ожиданием tμ и среднеквадратическим отклонением σμ= tμ
- 49. M|G|1 ?M|M|1
- 50. M|D|1 Время обслуживания не является случайным – tμ, среднеквадратическое отклонение σμ=0 Коэффициент вариации νμ= σμ/ tμ
- 51. M|G|1?M|D|1
- 52. Немарковские СМО Одноканальная СМО с произвольным потоком заявок и произвольным распределением времени обслуживания – G| G|
- 53. G| G| 1 с ∞ очередью Время обслуживания распределено по произвольному закону с мат. ожиданием tμ
- 54. G| G| 1 с ∞ очередью Время между заявками распределено по произвольному закону с мат. ожиданием
- 55. G|G|1 с бесконечной очередью Неравенство Файнберга
- 56. Пример В СМО поступают заявки в среднем через 15 мин, коэффициент вариации равен 0,4. Обслуживание происходит
- 57. Пример 16/25*(0,16+0,49)*2,5-0,4*0,84 ρ = 4/5 1,04-0,33 Woch=Loch/λ Woch=1,04/4=0,26 ч=15 мин
- 58. Пример Если входной поток – простейший, то Loch= 2,4 Loch = 16/25*(1+0,49)*2,5 Woch=2,4/4=0,6 ч=36 мин
- 59. Многоканальные немарковские СМО Среднее число занятых каналов kср=ρ
- 60. Многоканальные немарковские СМО Если каналов много (по крайней мере >5), то поток обслуживания практически близок к
- 61. Многоканальные немарковские СМО Когда входной поток заведомо не простейший В этом случае можно подобрать две одноканальные
- 62. «Худший» вариант (пессимистическая оценка) n-канальную СМО на п одноканальных На каждую СМО будет поступать поток Эрланга
- 63. «Лучший» вариант (оптимистическая оценка) n-канальную СМО одной одноканальной, но с интенсивностью потока обслуживания в n раз
- 65. Скачать презентацию











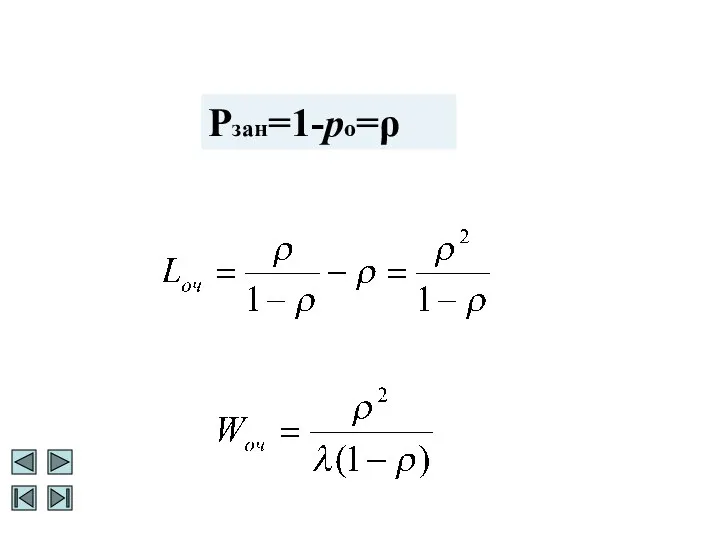






























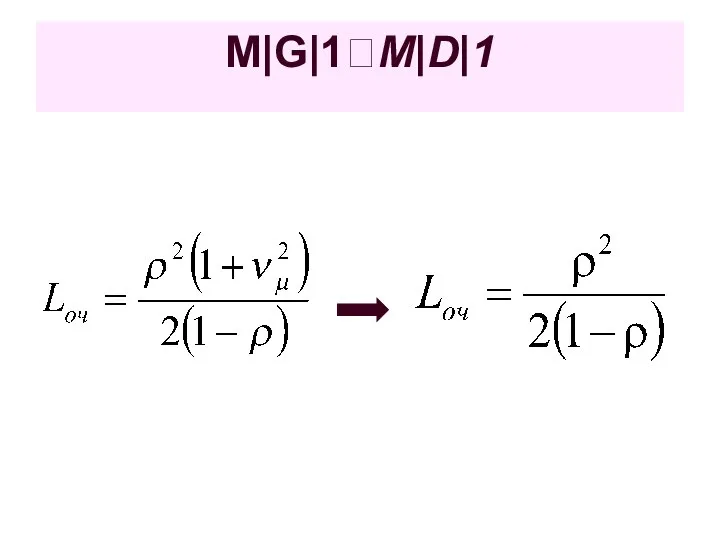












 Коммутационные перенапряжения
Коммутационные перенапряжения Информация о товаре
Информация о товаре Страхование ответственности производителей за качество продукции
Страхование ответственности производителей за качество продукции Сортировка. Алгоритмы сортировки
Сортировка. Алгоритмы сортировки «Орфография в загадках и отгадках» Автор презентации: Токмакова Вероника ученица 4 «А» класса МОУ СОШ № 5
«Орфография в загадках и отгадках» Автор презентации: Токмакова Вероника ученица 4 «А» класса МОУ СОШ № 5 Одежда в эпоху классицизма
Одежда в эпоху классицизма Патогенетическая терапия
Патогенетическая терапия Аттестационная работа. «Если ехать Вам случиться», создание краткого справочника – путеводителя
Аттестационная работа. «Если ехать Вам случиться», создание краткого справочника – путеводителя Создание программных приложений на базе технологии Entity Framework
Создание программных приложений на базе технологии Entity Framework Стратегический менеджмент Стратегический менеджмент ___________________ Тема 1. Сущность стратегического менеджмента
Стратегический менеджмент Стратегический менеджмент ___________________ Тема 1. Сущность стратегического менеджмента  Организация учебного процесса студентов в УрФУ
Организация учебного процесса студентов в УрФУ Бабушка воюет с разбойниками - презентация для начальной школы
Бабушка воюет с разбойниками - презентация для начальной школы История развития и современное состояние оздоровительной и адаптивной физической культуры
История развития и современное состояние оздоровительной и адаптивной физической культуры Введение в специальность
Введение в специальность Магазин игрушек. Игра
Магазин игрушек. Игра Проценты в гостях в Простоквашино - презентация по Алгебре
Проценты в гостях в Простоквашино - презентация по Алгебре Немецкая классическая философия
Немецкая классическая философия Динамика развития группы
Динамика развития группы Внеклассное мероприятие по немецкому языку в 5-7 классах
Внеклассное мероприятие по немецкому языку в 5-7 классах От культурно-образовательных проектов к культурно-образовательным практикам
От культурно-образовательных проектов к культурно-образовательным практикам Средневековая архитектура Романский стиль
Средневековая архитектура Романский стиль Игры на развитие внимания
Игры на развитие внимания Арифметическая прогрессия - презентация по Алгебре
Арифметическая прогрессия - презентация по Алгебре Губернаторский проект "Решаем вместе" - ремонт футбольного поля МОУ "Гимназия № 3"
Губернаторский проект "Решаем вместе" - ремонт футбольного поля МОУ "Гимназия № 3" Информационная безопасность. Решения DEPO Security Systems
Информационная безопасность. Решения DEPO Security Systems Тест по русскому языку 2 класс Учитель начальных классов МОУ СОШ №4 г.Нурлат РТ Миндубае
Тест по русскому языку 2 класс Учитель начальных классов МОУ СОШ №4 г.Нурлат РТ Миндубае Политика и власть
Политика и власть Средства радиосвязи. Поисковый Отряд ЛизаАлерт, Москва
Средства радиосвязи. Поисковый Отряд ЛизаАлерт, Москва