Содержание
- 2. Расчет на прочность. Расчёт ведётся по величине фактических максимальных напряжений, возникающих в опасной точке нагруженной конструкции
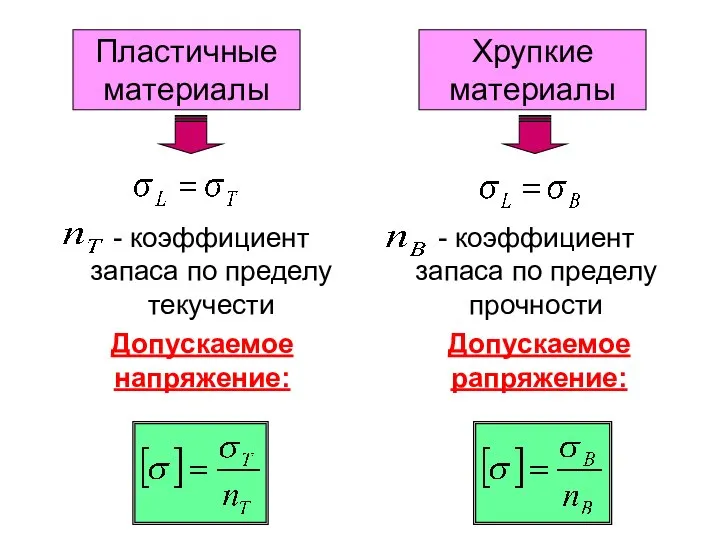
- 3. Пластичные материалы - коэффициент запаса по пределу текучести Допускаемое напряжение: Хрупкие материалы - коэффициент запаса по
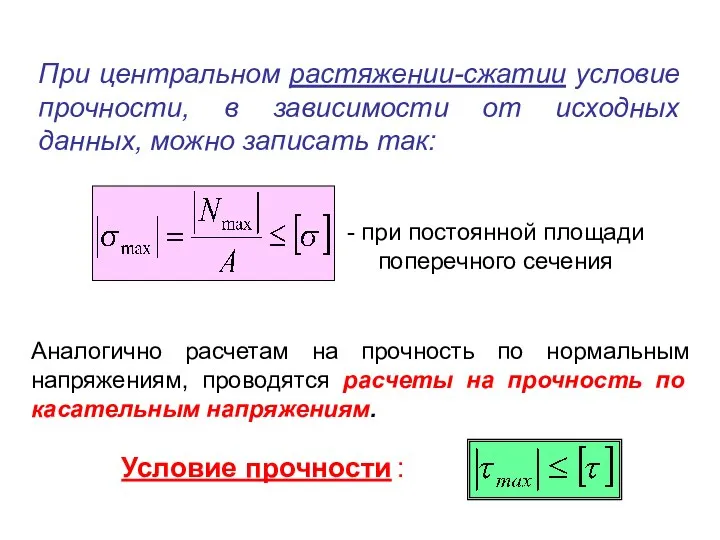
- 4. При центральном растяжении-сжатии условие прочности, в зависимости от исходных данных, можно записать так: Аналогично расчетам на
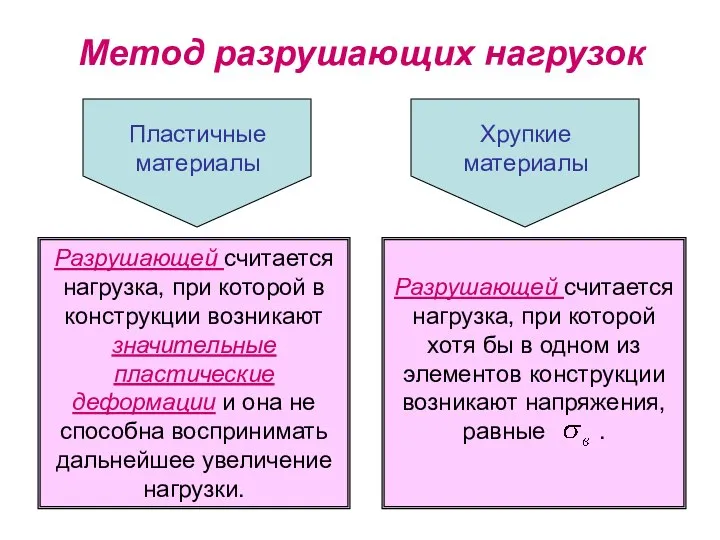
- 5. Метод разрушающих нагрузок Разрушающей считается нагрузка, при которой в конструкции возникают значительные пластические деформации и она
- 6. Расчеты на прочность бывают двух видов: проверочный проектировочный При этом решается одна из трех задач: проверка
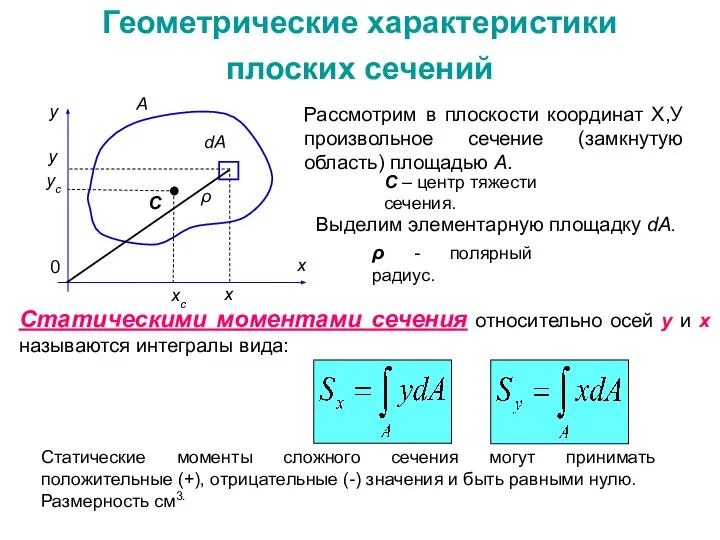
- 7. Геометрические характеристики плоских сечений Рассмотрим в плоскости координат Х,У произвольное сечение (замкнутую область) площадью А. C
- 8. Осевые и полярный моменты инерции могут принимать положительные и равные нулю значения. Размерность: [ см4 ].
- 9. Центробежным моментом инерции сечения называется интеграл вида: Центробежный момент инерции может принимать положительные, отрицательные или равные
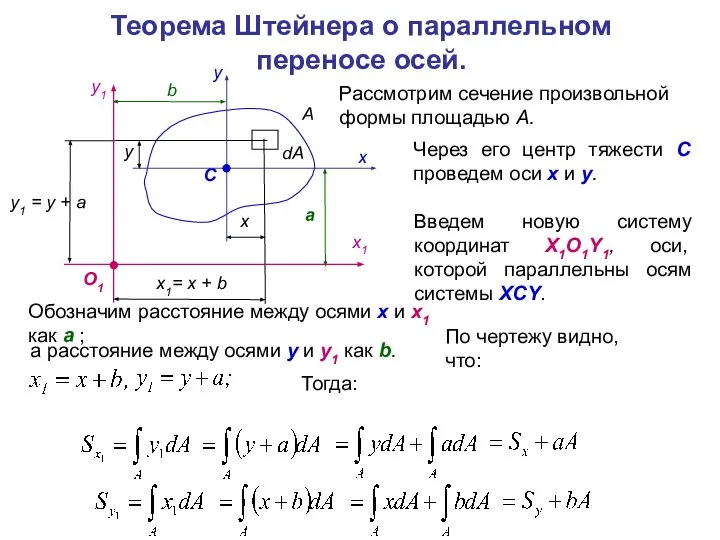
- 10. Теорема Штейнера о параллельном переносе осей. Рассмотрим сечение произвольной формы площадью А. Через его центр тяжести
- 11. Следствие: если то если то Оси, относительно которых статические моменты равны нулю, называются центральными. Точка пересечения
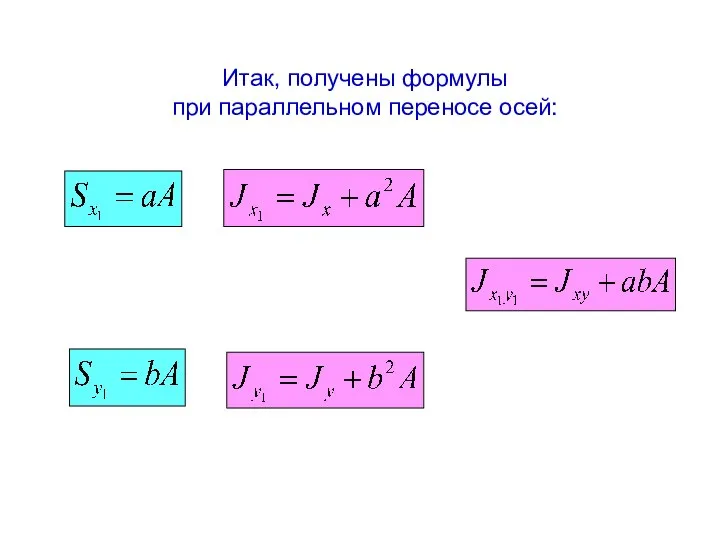
- 12. Итак, получены формулы при параллельном переносе осей:
- 13. Осевые моменты инерции простых сечений Пример. Прямоугольник. Рассмотрим прямоугольник с вертикальным ребром h и горизонтальным ребром
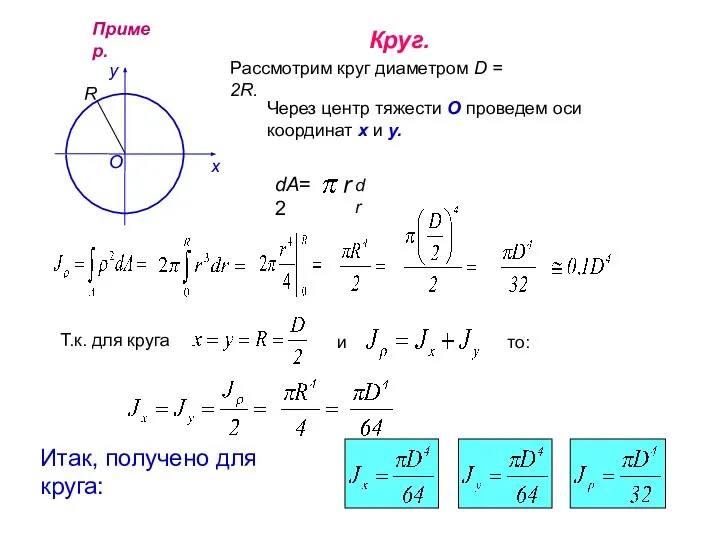
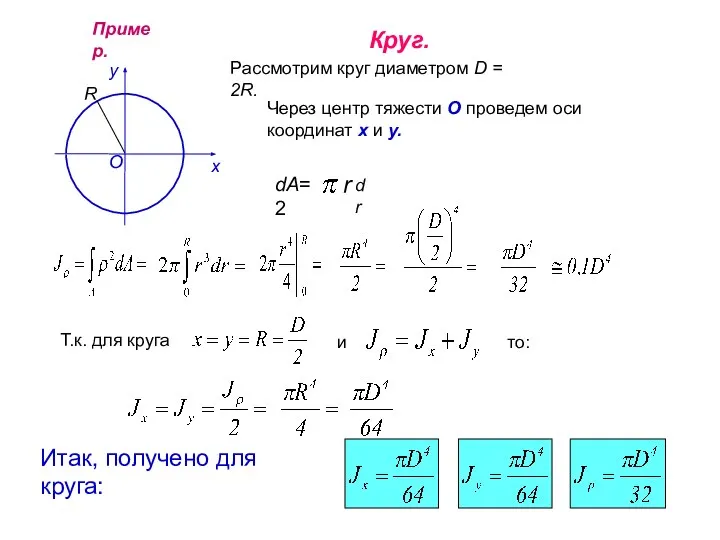
- 14. Пример. Круг. Рассмотрим круг диаметром D = 2R. Через центр тяжести О проведем оси координат х
- 15. Моменты сопротивления сечений Осевым моментом сопротивления сечения изгибу называется отношение осевого момента инерции к наибольшему расстоянию
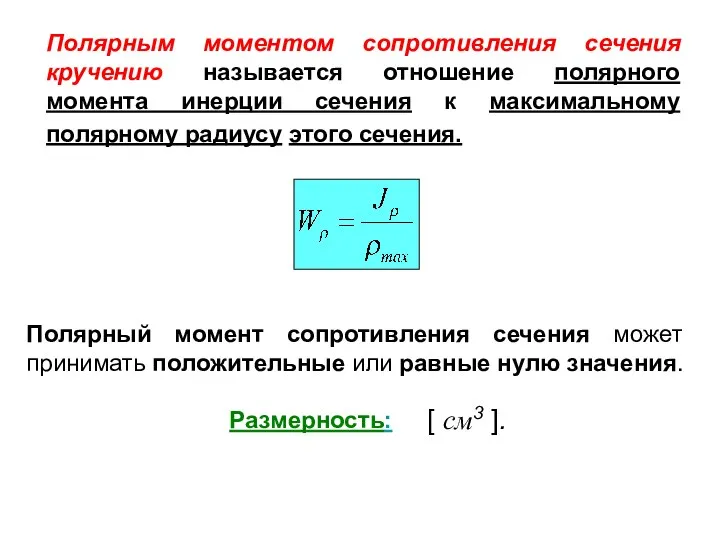
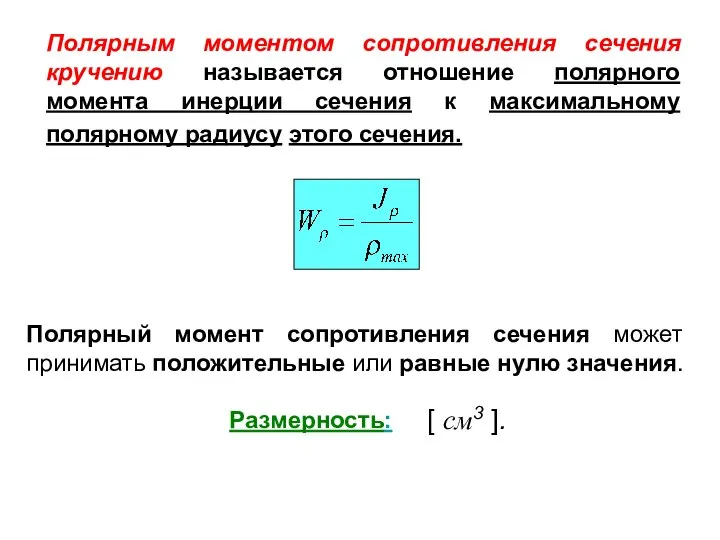
- 16. Полярным моментом сопротивления сечения кручению называется отношение полярного момента инерции сечения к максимальному полярному радиусу этого
- 17. Рассмотрим моменты сопротивления некоторых простых сечений. О Прямоугольное сечение. Итак, получено: Круглое сечение. О Итак, получено:
- 18. Осевые моменты инерции простых сечений Пример. Прямоугольник. Рассмотрим прямоугольник с вертикальным ребром h и горизонтальным ребром
- 19. Пример. Круг. Рассмотрим круг диаметром D = 2R. Через центр тяжести О проведем оси координат х
- 20. Моменты сопротивления сечений Осевым моментом сопротивления сечения изгибу называется отношение осевого момента инерции к наибольшему расстоянию
- 21. Полярным моментом сопротивления сечения кручению называется отношение полярного момента инерции сечения к максимальному полярному радиусу этого
- 23. Скачать презентацию










 DC sweep Parameter sweep Temperature sweep. Виды автоматического анализа в Multisim
DC sweep Parameter sweep Temperature sweep. Виды автоматического анализа в Multisim Итоги учебно-воспитательная работа в лицее за 2014-2015 учебный год. Заместитель директора по УВР Попова Л.А.
Итоги учебно-воспитательная работа в лицее за 2014-2015 учебный год. Заместитель директора по УВР Попова Л.А.  Почему интернет-реклама не работает
Почему интернет-реклама не работает Организация сети передачи данных по энергосетям с применением PLC технологии
Организация сети передачи данных по энергосетям с применением PLC технологии Экономика Санкт-Петербурга Работу представил ученик 9 “Г” класса: Саликов Никита
Экономика Санкт-Петербурга Работу представил ученик 9 “Г” класса: Саликов Никита  Ҡаҙ өмәһе
Ҡаҙ өмәһе Рулевое управление тракторов
Рулевое управление тракторов Воскресная школа «Наши родители помогают нам учиться». Класс «Выбирай истину» (4-7 лет)
Воскресная школа «Наши родители помогают нам учиться». Класс «Выбирай истину» (4-7 лет) Искусственные каменные материалы на основе вяжущих веществ. Силикатный кирпич и силикатобетонные изделия
Искусственные каменные материалы на основе вяжущих веществ. Силикатный кирпич и силикатобетонные изделия «Мой друг». Хорошая книга, мой спутник, мой друг, С тобой интересным бывает досуг. Мы время отлично проводим вдвоём И наш разговор потихоньку ведём… Ты мне говоришь про дела смельчаков, Про злобных врагов и смешных чудаков, Про тайны Земли и движен
«Мой друг». Хорошая книга, мой спутник, мой друг, С тобой интересным бывает досуг. Мы время отлично проводим вдвоём И наш разговор потихоньку ведём… Ты мне говоришь про дела смельчаков, Про злобных врагов и смешных чудаков, Про тайны Земли и движен Деревянные конструкции
Деревянные конструкции Насколько выгодно заниматься социальным бизнесом?
Насколько выгодно заниматься социальным бизнесом? Фольклорный коллектив «Бура́новские ба́бушки»
Фольклорный коллектив «Бура́новские ба́бушки» Виртуальный музей КГБПОУ «Бийский педагогический колледж»
Виртуальный музей КГБПОУ «Бийский педагогический колледж» Pascal-Модули C-Библиотеки
Pascal-Модули C-Библиотеки Інформаційна війна та маніпулювання
Інформаційна війна та маніпулювання Наша родина россия
Наша родина россия Java Best Practice. Лучшие практики разработки на Java
Java Best Practice. Лучшие практики разработки на Java Электроснабжение механического цеха завода подъемно-транспортного оборудования
Электроснабжение механического цеха завода подъемно-транспортного оборудования Тема 2. Экологический кризис: проблемы глобальных городов
Тема 2. Экологический кризис: проблемы глобальных городов  Промежуточный мозг Diencephalon
Промежуточный мозг Diencephalon Метод дисконтирования денежных потоков
Метод дисконтирования денежных потоков Физиология микроорганизмов (дыхание, размножение)
Физиология микроорганизмов (дыхание, размножение) Муниципальное образовательное учреждение Основная общеобразовательная школа №116 имени В.П.Чкалова Экономические расчеты в прое
Муниципальное образовательное учреждение Основная общеобразовательная школа №116 имени В.П.Чкалова Экономические расчеты в прое 1941-1945гг 1941-1945гг
1941-1945гг 1941-1945гг  Богатые Домашнее задание: параграф
Богатые Домашнее задание: параграф Загальні засади конституційно-правового статусу людини і громадянина в Україні
Загальні засади конституційно-правового статусу людини і громадянина в Україні Interaction of the atmosphere with underlying surfaces
Interaction of the atmosphere with underlying surfaces