Содержание
- 2. Зачем нужна формальная семантика? Чтобы точно знать возможности языка программирования. Чтобы доказывать корректность программы, а не
- 3. Эквивалентные преобразования программы Зная, что if true then C1 else C2 делает тоже самое, что и
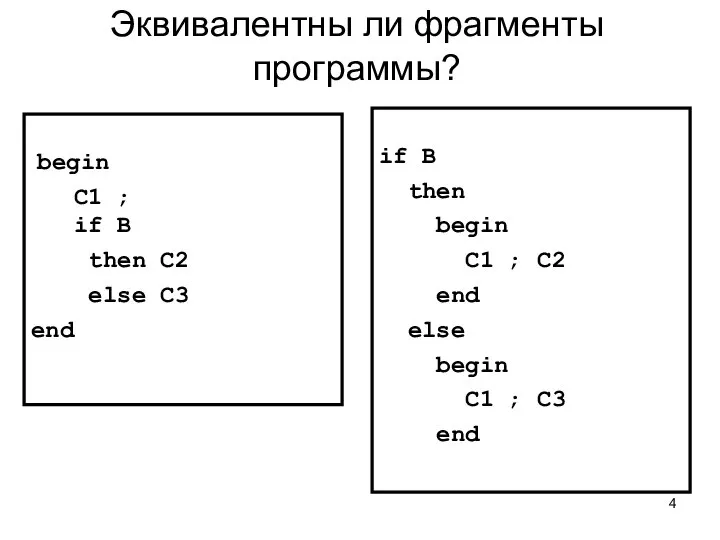
- 4. Эквивалентны ли фрагменты программы? begin C1 ; if B then C2 else C3 end if B
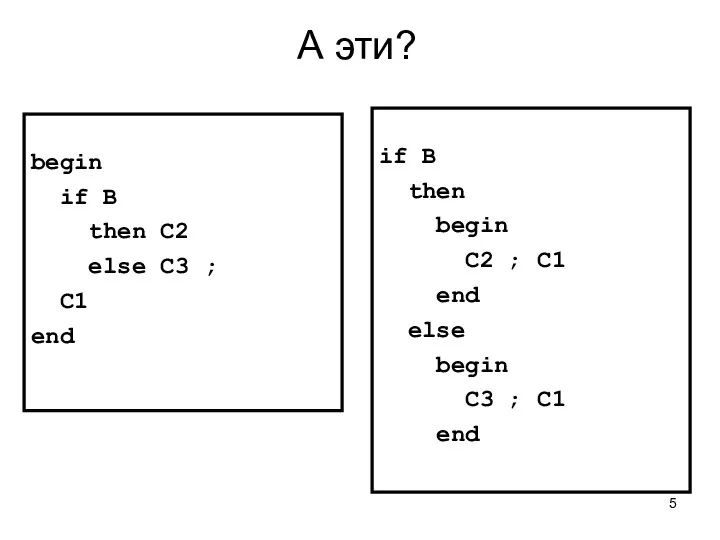
- 5. А эти? begin if B then C2 else C3 ; C1 end if B then begin
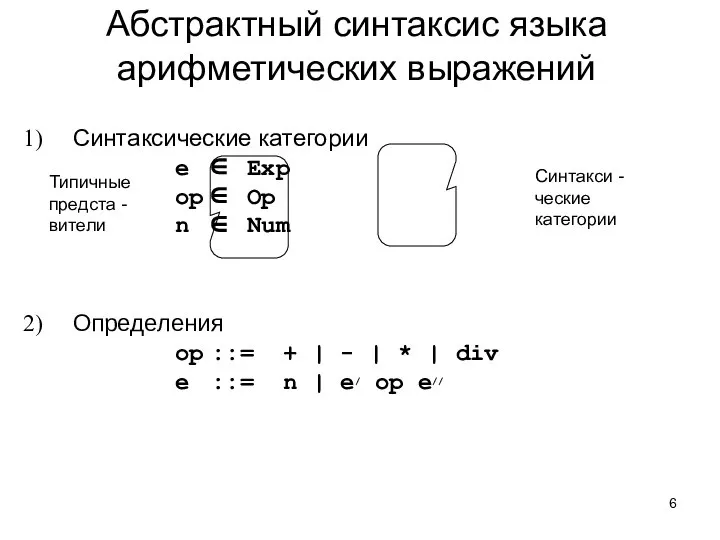
- 6. Синтаксические категории е ∈ Exp op ∈ Op n ∈ Num Определения op ::= + |
- 7. Методы определения семантики Конкретная операционная семантика Естественная семантика Вычислительная (структурно – операционная) семантика Денотационная семантика
- 8. Конкретнтая операционная семантика языка Exp topostfix(N,S,[N|S]) :- number(N). topostfix(E,S,R) :- E =.. [Op,A,B], member(Op,[+,-,*,/]), topostfix(A,[Op|S],S1), topostfix(B,S1,R).
- 9. Естественная семантика Это аксиоматическая система, определяющая смысл каждой конструкции языка в виде вычисляемого ею значения. Определим
- 10. Правила, определяющие естественную семантику языка арифметических выражений Правило CR Правило OpR n ⇒ n e ⇒
- 11. Пусть нужно вычислить значение выражения 3 * 4 + 8 div (4 – 2). Это сумма,
- 12. В конце концов, получив численную константу применим правила CR: Вычисление значения арифметических выражений (продолжение) 3 ⇒
- 13. Реализация естественной семантики языка Exp eval(N,N) :- number(N). eval(E,R) :- E =.. [Op,E1,E2], member(Op,[+,-,*,/]), eval(E1,R1), eval(E2,R2),
- 14. Индукция Свойства семантики языка программирования можно доказывать по индукции. Метод математической индукции: Чтобы доказать свойство P(x)
- 15. Пример Пусть нужно доказать, что сумма первых n натуральных чисел равна n * (n+1) div 2,
- 16. Структурная индукция Метод математической индукции применим к натуральным числам потому, что их множество определяется по индукции:
- 17. Закон « map после (++)» Для всех списков xs, ys и функций f выполняется равенство: map
- 19. Теорема. Отношение ⇒ для языка Exp является функцией Для всех выражений е ∈ Exp справедливо, что
- 20. Первый случай Если n ⇒ v, а для вычисления v мы могли использовать только правило CR
- 22. Скачать презентацию



![Конкретнтая операционная семантика языка Exp topostfix(N,S,[N|S]) :- number(N). topostfix(E,S,R) :- E](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1374335/slide-7.jpg)












 Семь раз отмерь, один раз слейся (3). Анализ сделки по приобретению Jaguar, Land Rover компанией Tata Motors
Семь раз отмерь, один раз слейся (3). Анализ сделки по приобретению Jaguar, Land Rover компанией Tata Motors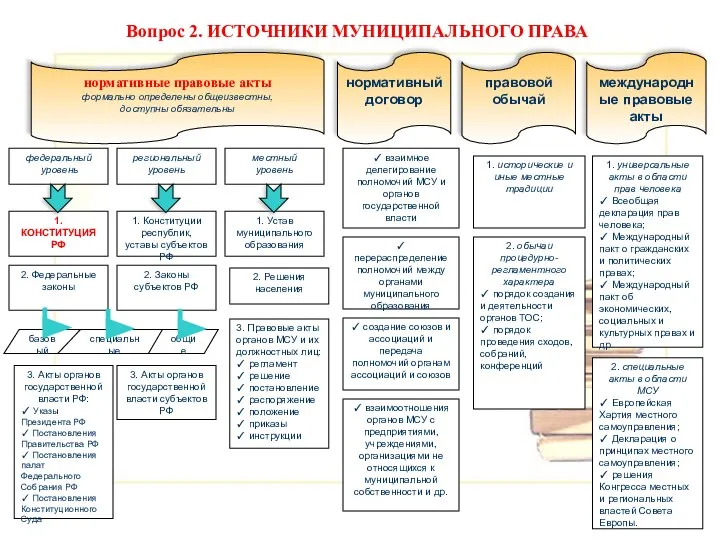 Источники муниципального права
Источники муниципального права Функціональні матеріали для високоенергетичної електроніки
Функціональні матеріали для високоенергетичної електроніки ОБЩЕСТВЕННОЕ ПРОИЗВОДСТВО
ОБЩЕСТВЕННОЕ ПРОИЗВОДСТВО Электромагнитные поля и волны
Электромагнитные поля и волны  Особенности планирования и организации уроков рисования. Основы цветоведения. Методика ознакомления с живописью
Особенности планирования и организации уроков рисования. Основы цветоведения. Методика ознакомления с живописью Татаро-башкирская народная культура
Татаро-башкирская народная культура Эталонны
Эталонны  Meine Traumreise
Meine Traumreise Қонақ үйдегі (мейрамханадағы) қызмет көрсету мәдениеті мен сапасын арттыруды ұйымдастыру
Қонақ үйдегі (мейрамханадағы) қызмет көрсету мәдениеті мен сапасын арттыруды ұйымдастыру Зал № 9. Натюрморты По благородной простоте и изяществу натюрморты И.И.Левитана не имеют себе равных в русской пейзажной живопи
Зал № 9. Натюрморты По благородной простоте и изяществу натюрморты И.И.Левитана не имеют себе равных в русской пейзажной живопи 9 cooperarea în logistică
9 cooperarea în logistică Наружные лестницы
Наружные лестницы matematicheskiy_breyn_2019
matematicheskiy_breyn_2019 Алгоритмы. Задачи алгоритмизации
Алгоритмы. Задачи алгоритмизации Борьба организма с инфекцией. Подготовила: Ученица 8 класса А Чиндяскина Александра.
Борьба организма с инфекцией. Подготовила: Ученица 8 класса А Чиндяскина Александра. 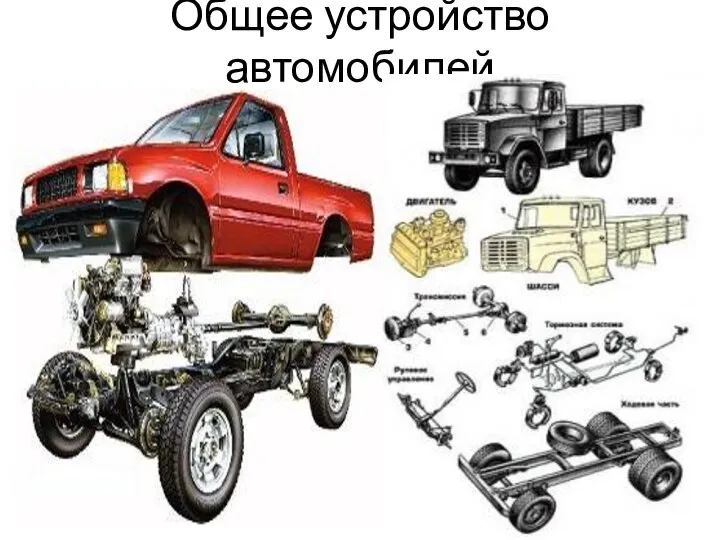 Общее устройство автомобилей
Общее устройство автомобилей Как оценивать успехи школьников «Когда человек не знает, к какой пристани он держит путь, для него ни один ветер не будет попутным»
Как оценивать успехи школьников «Когда человек не знает, к какой пристани он держит путь, для него ни один ветер не будет попутным» Экологические проблемы Урала
Экологические проблемы Урала  Национальная политике в 30-е годы
Национальная политике в 30-е годы Клиническая характеристика психоактивных веществ (ПАВ) Психоактивное вещество- вещество природного или синтетического происхожд
Клиническая характеристика психоактивных веществ (ПАВ) Психоактивное вещество- вещество природного или синтетического происхожд Презентация "Дело в шляпе" - скачать презентации по МХК
Презентация "Дело в шляпе" - скачать презентации по МХК Знакомство с программой «Кадровый Резерв»
Знакомство с программой «Кадровый Резерв» Урок 62 2 класс
Урок 62 2 класс Алгебраические дроби
Алгебраические дроби Презентация "Рембрандт ван Рейн (1606-1669)" - скачать презентации по МХК
Презентация "Рембрандт ван Рейн (1606-1669)" - скачать презентации по МХК Процедура прохождения допинг-контроля. Права и обязанности спортсменов
Процедура прохождения допинг-контроля. Права и обязанности спортсменов Каменные стены МКД
Каменные стены МКД