Содержание
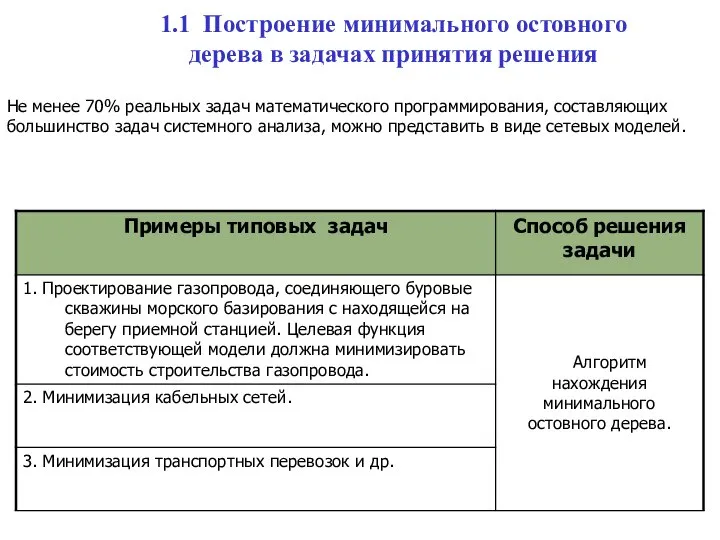
- 2. Не менее 70% реальных задач математического программирования, составляющих большинство задач системного анализа, можно представить в виде
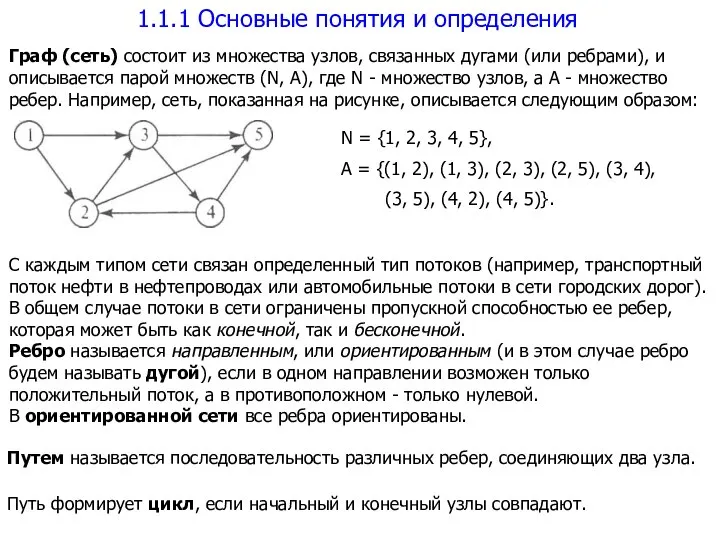
- 3. 1.1.1 Основные понятия и определения Граф (сеть) состоит из множества узлов, связанных дугами (или ребрами), и
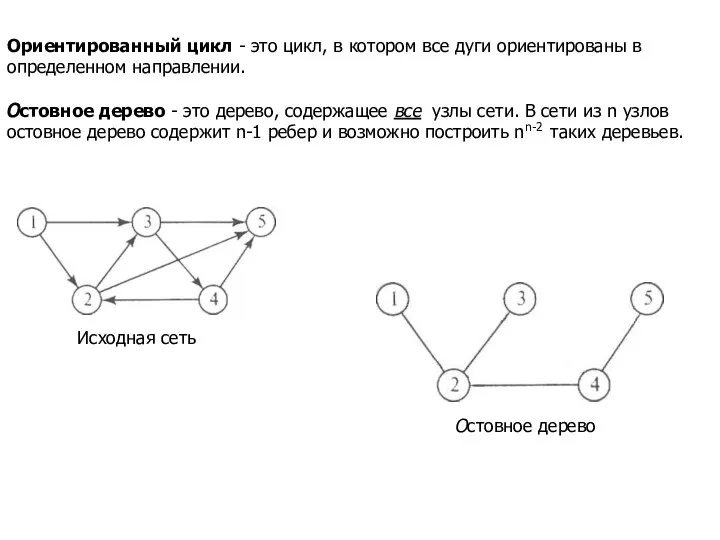
- 4. Ориентированный цикл - это цикл, в котором все дуги ориентированы в определенном направлении. Остовное дерево -
- 5. 1.1.2 Алгоритм построения минимального остовного дерева Алгоритм построения минимального остовного дерева предполагает соединение всех узлов сети
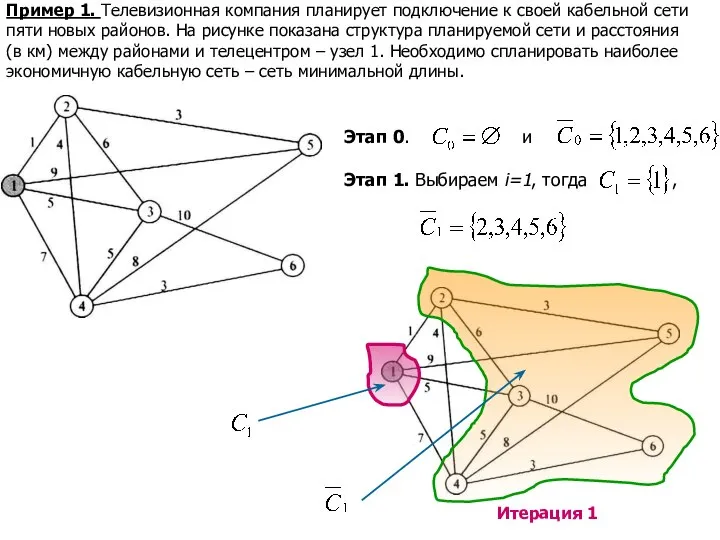
- 7. Пример 1. Телевизионная компания планирует подключение к своей кабельной сети пяти новых районов. На рисунке показана
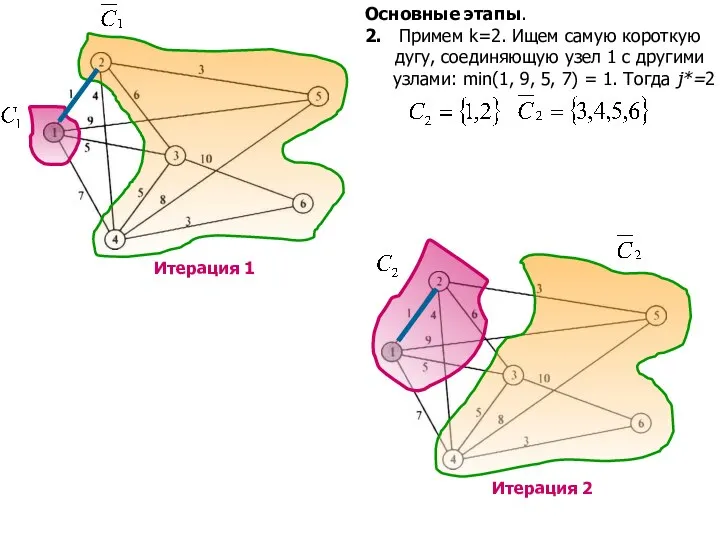
- 8. Основные этапы. 2. Примем k=2. Ищем самую короткую дугу, соединяющую узел 1 с другими узлами: min(1,
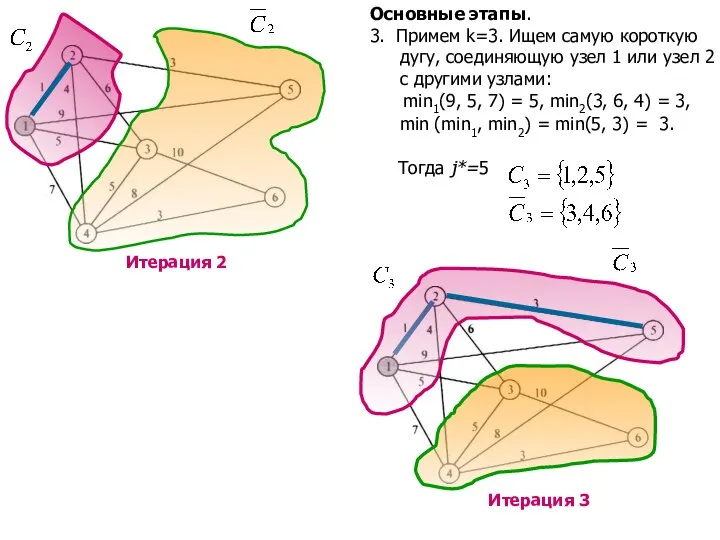
- 9. Основные этапы. 3. Примем k=3. Ищем самую короткую дугу, соединяющую узел 1 или узел 2 с
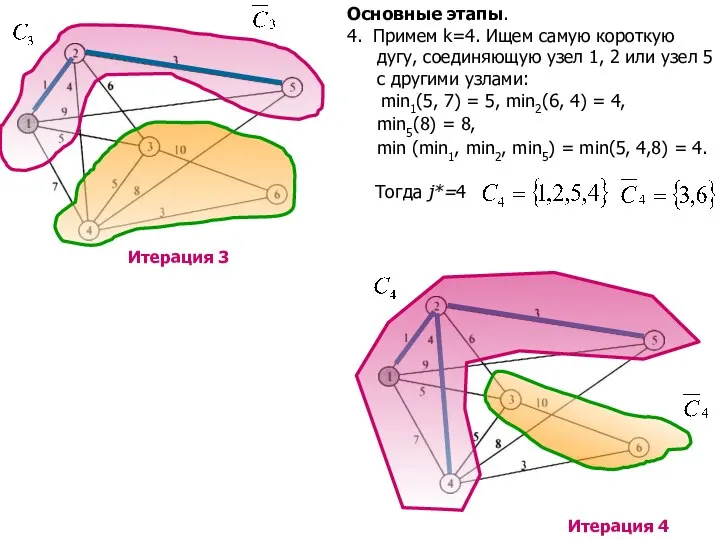
- 10. Основные этапы. 4. Примем k=4. Ищем самую короткую дугу, соединяющую узел 1, 2 или узел 5
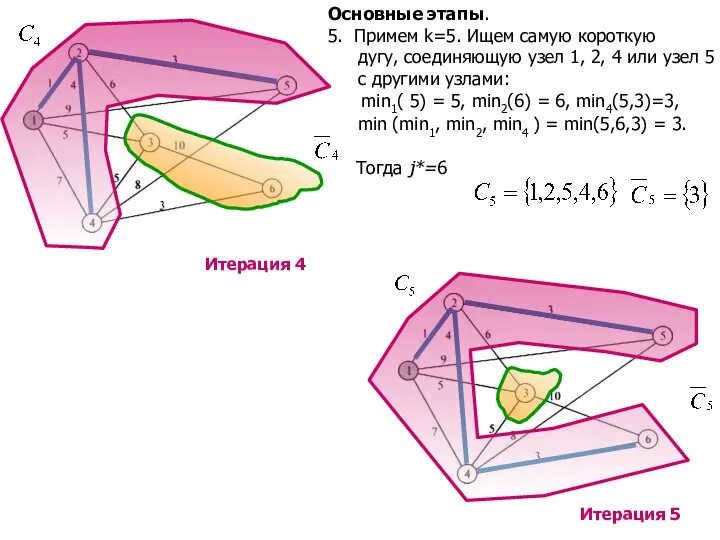
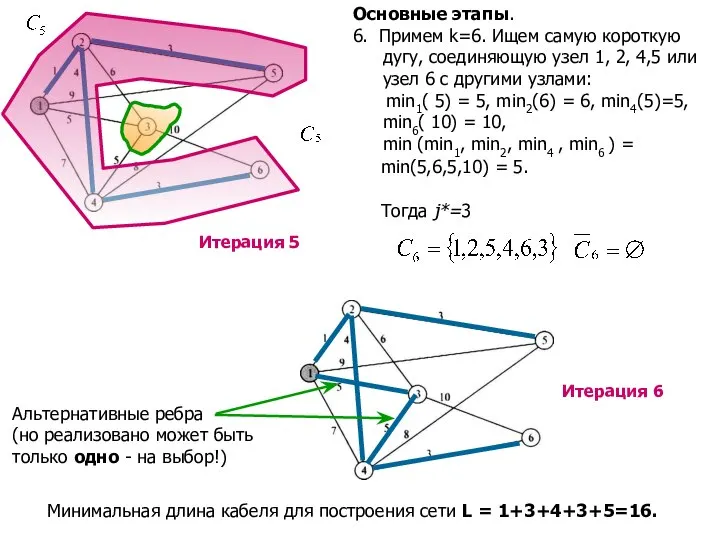
- 11. Основные этапы. 5. Примем k=5. Ищем самую короткую дугу, соединяющую узел 1, 2, 4 или узел
- 12. Альтернативные ребра (но реализовано может быть только одно - на выбор!) Минимальная длина кабеля для построения
- 13. 1.1.3. Задание для самостоятельной работы Решить задачу из Примера 1 при следующих условиях: а) узлы 1
- 14. 1.2 Сетевые модели: Алгоритмы поиска кратчайшего пути Представленные здесь алгоритмы поиска кратчайшего пути справедливы как для
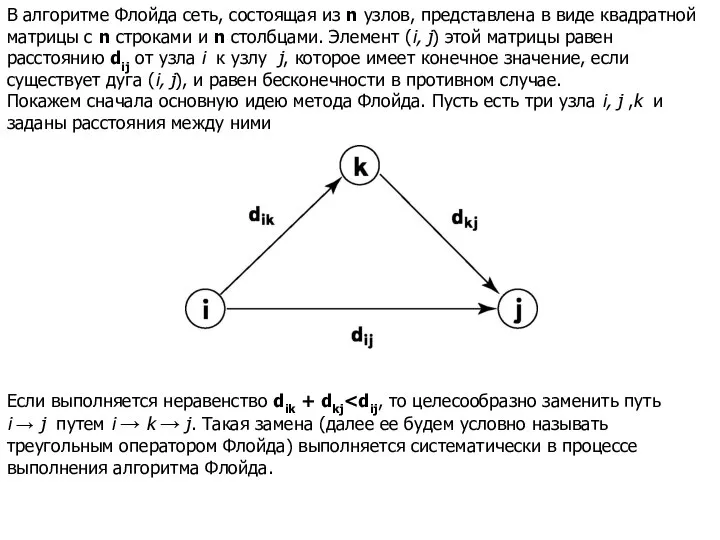
- 15. В алгоритме Флойда сеть, состоящая из n узлов, представлена в виде квадратной матрицы с n строками
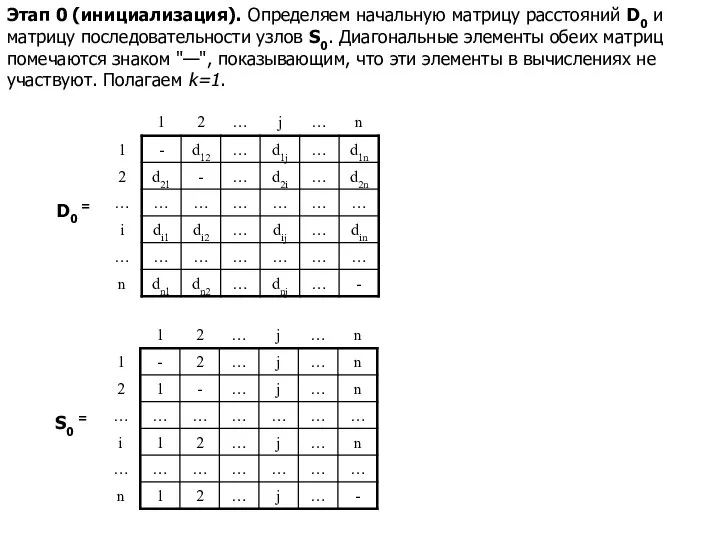
- 16. Этап 0 (инициализация). Определяем начальную матрицу расстояний D0 и матрицу последовательности узлов S0. Диагональные элементы обеих
- 17. Основной этап k. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Двигаясь
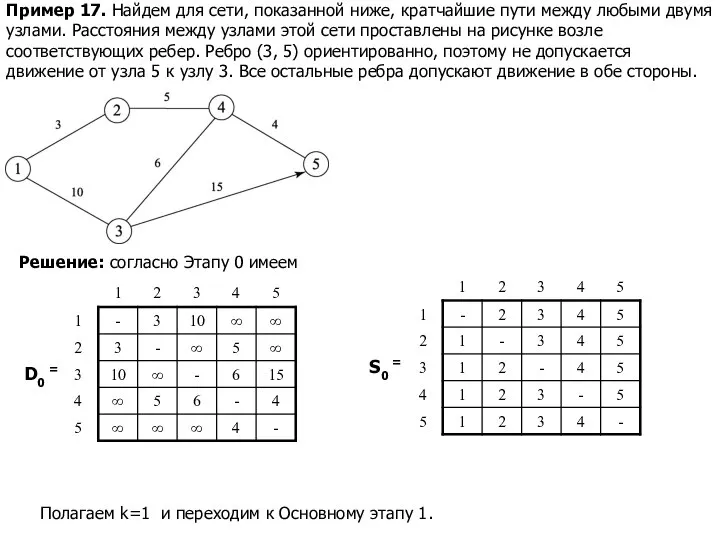
- 18. Пример 17. Найдем для сети, показанной ниже, кратчайшие пути между любыми двумя узлами. Расстояния между узлами
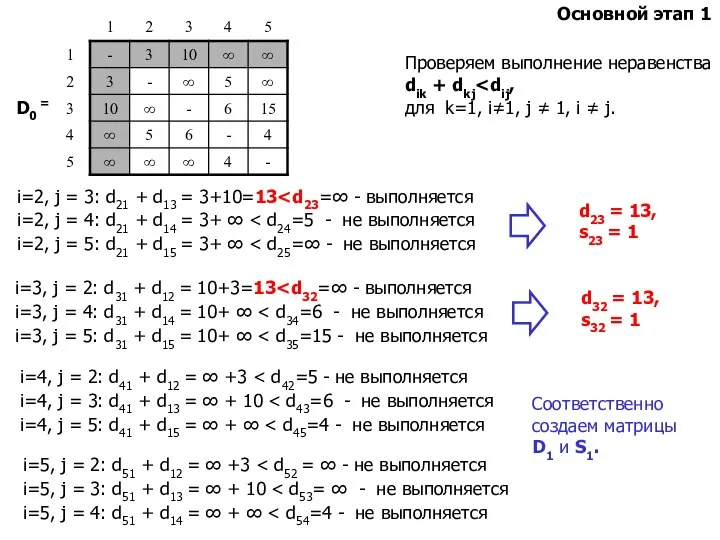
- 19. D0 = Проверяем выполнение неравенства dik + dkj для k=1, i≠1, j ≠ 1, i ≠
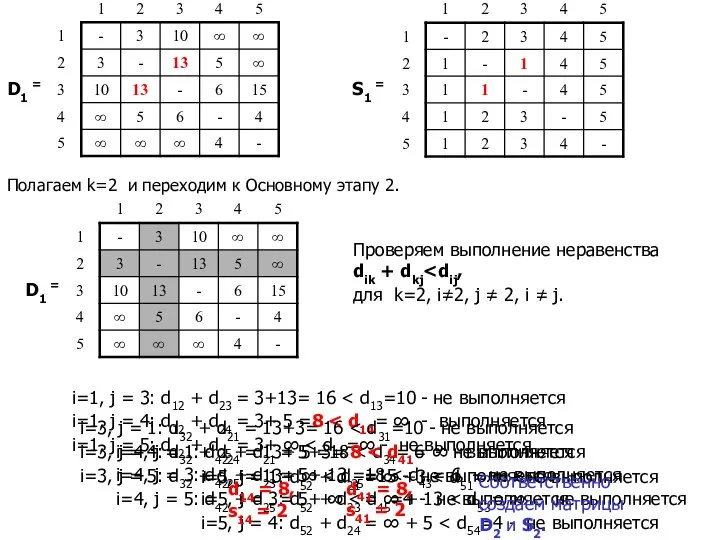
- 20. D1 = S1 = Полагаем k=2 и переходим к Основному этапу 2. D1 = Проверяем выполнение
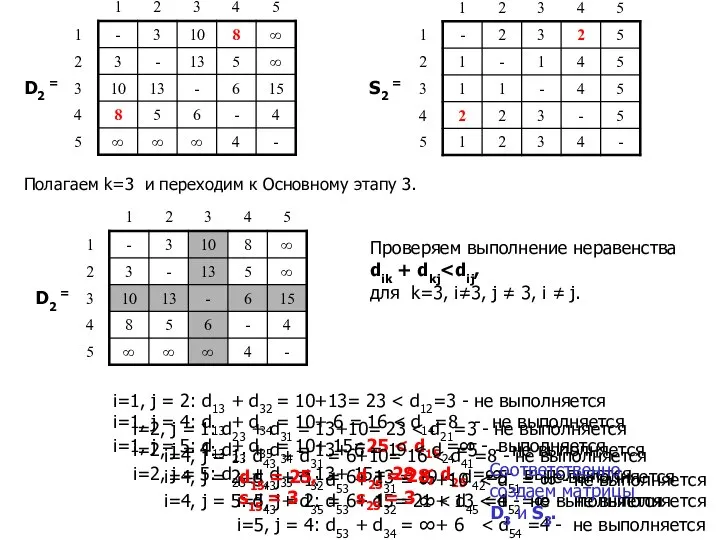
- 21. D2 = S2 = Полагаем k=3 и переходим к Основному этапу 3. Проверяем выполнение неравенства dik
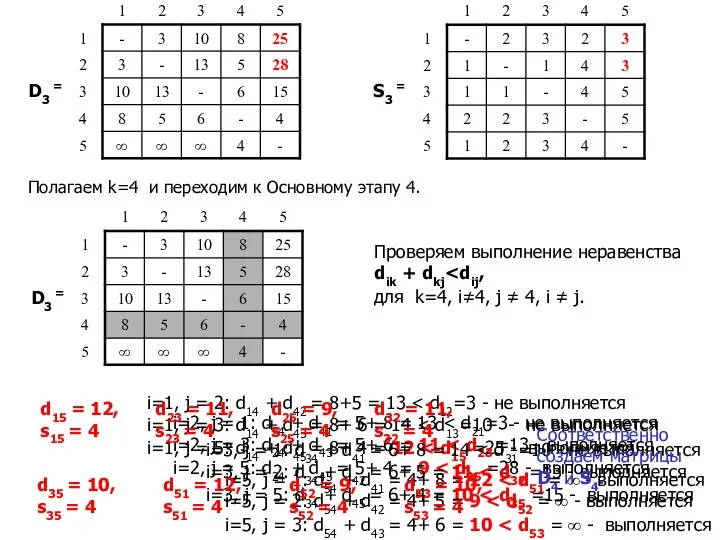
- 22. D3 = S3 = Полагаем k=4 и переходим к Основному этапу 4. Проверяем выполнение неравенства dik
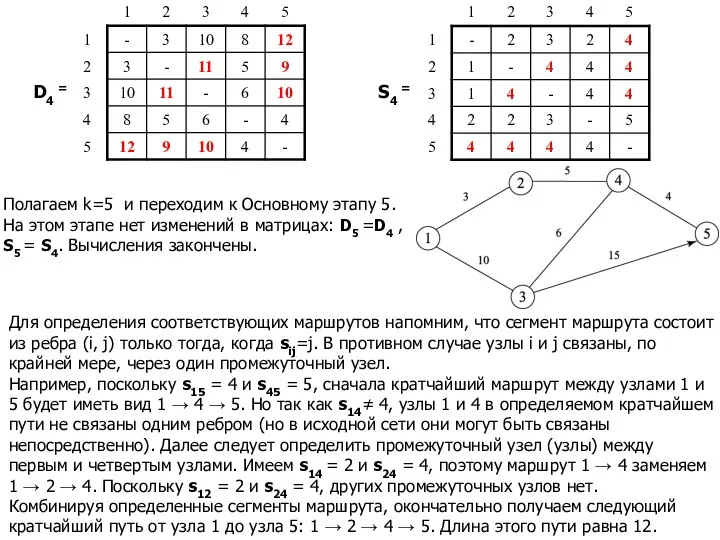
- 23. D4 = S4 = Полагаем k=5 и переходим к Основному этапу 5. На этом этапе нет
- 25. Скачать презентацию





 Армянские народные танцы
Армянские народные танцы Лабораторная работа №2. Построение системы кодирования информации с использованием языка Ассемблер
Лабораторная работа №2. Построение системы кодирования информации с использованием языка Ассемблер Франкенштейн - доктор любви. Игра
Франкенштейн - доктор любви. Игра Схема внешнего электроснабжения ОГР
Схема внешнего электроснабжения ОГР Вопросы симметрии в математике и архитектуре
Вопросы симметрии в математике и архитектуре Тема 10. Міжнародні науково-технічні відносини
Тема 10. Міжнародні науково-технічні відносини Презентация "Экономика как наука" - скачать презентации по Экономике
Презентация "Экономика как наука" - скачать презентации по Экономике Башкирские народные музыкальные инструменты
Башкирские народные музыкальные инструменты Агентство здоровой жизни
Агентство здоровой жизни Художественные символы народов мира_
Художественные символы народов мира_ ПРОЕКТ «Символика резного декора деревянного дома». Дисциплина «Народный орнамент» специальность: 072601 «Декоративно-прикладное
ПРОЕКТ «Символика резного декора деревянного дома». Дисциплина «Народный орнамент» специальность: 072601 «Декоративно-прикладное  Основы механики деформации горных пород. Тема 3
Основы механики деформации горных пород. Тема 3 Фёдор Михайлович Достоевский
Фёдор Михайлович Достоевский 3D-мониторы
3D-мониторы Знакомство с творчеством И. И. Шишкина «Сказка о лесном художнике»
Знакомство с творчеством И. И. Шишкина «Сказка о лесном художнике»  Технологии подготовки и проведения выставки
Технологии подготовки и проведения выставки Основы графической грамоты
Основы графической грамоты Слоговые таблицы к урокам обучения грамоте
Слоговые таблицы к урокам обучения грамоте Презентация Переход на международную систему бакалавра и магистра: благо или новые проблемы?
Презентация Переход на международную систему бакалавра и магистра: благо или новые проблемы? Современное состояние индустрии туризма
Современное состояние индустрии туризма  Бионика, как наука
Бионика, как наука Факторы, влияющие на надежность радиоэлектронных средств
Факторы, влияющие на надежность радиоэлектронных средств Презентация на тему Флаг России - символ государственности в формате powerpoint.ppt
Презентация на тему Флаг России - символ государственности в формате powerpoint.ppt Узоры из листьев 2Б 2019
Узоры из листьев 2Б 2019 Умные города на примере Цюриха и Ганьчжоу
Умные города на примере Цюриха и Ганьчжоу Индуизм. Направления индуизма
Индуизм. Направления индуизма Метод оценки качества, основанный на иерархической модели
Метод оценки качества, основанный на иерархической модели Машины постоянного тока
Машины постоянного тока