Содержание
- 2. Приведение записи задачи к каноническому виду Рассмотрим в качестве исходной задачу определения оптимальной производственной программы, записанную
- 4. Убедимся в том, что мы располагаем неотрицательным базисным решением. Признак наличия такого решения следующий: в каждом
- 5. Как получить неотрицательное базисное решение 1. Приведение к каноническому виду симметричной задачи на максимум Z позволяет
- 6. Что представляет собой базисное решение Каждый вектор единичной подматрицы образован коэффициентами переменных, которые именуются базисными. Остальные
- 7. Как реализуется симплекс-метод Получив начальное базисное решение, проверяем запись целевой функции. Если значение целевой функции нельзя
- 8. Как определить, что оптимум достигнут Через конечное число шагов получаем такую запись целевой функции, которая подтверждает
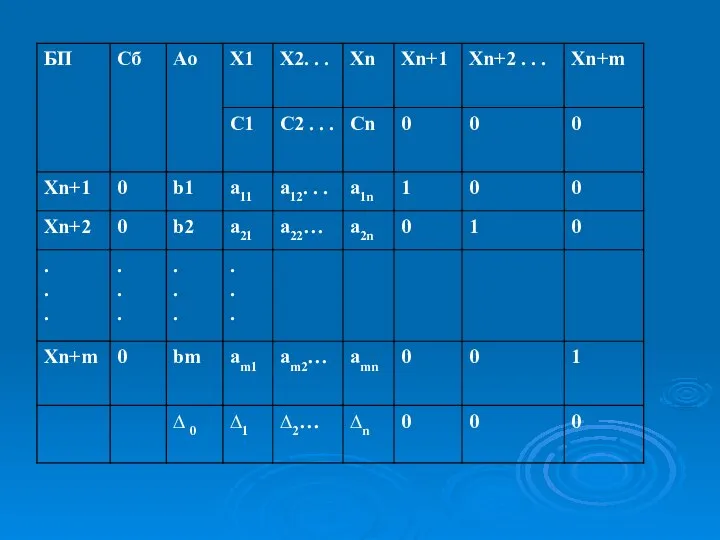
- 9. Что представляет собой симплексная таблица Симплексная таблица является компактной записью решения задачи симплекс-методом. Для ее заполнения
- 11. В данной таблице: БП – совокупность базисных переменных; – вектор коэффициентов, стоящих в целевой функции при
- 12. Процедура начинается с анализа заключительной строки таблицы, именуемой индексной, строкой оценок Если в данной строке при
- 13. Среди отрицательных при решении задачи на максимум (среди положительных при решении на min) выбираем наибольшую по
- 14. Как заполнить новую симплексную таблицу Изменяем состав базисных переменных, а также состав компонентов вектора Замену определяет
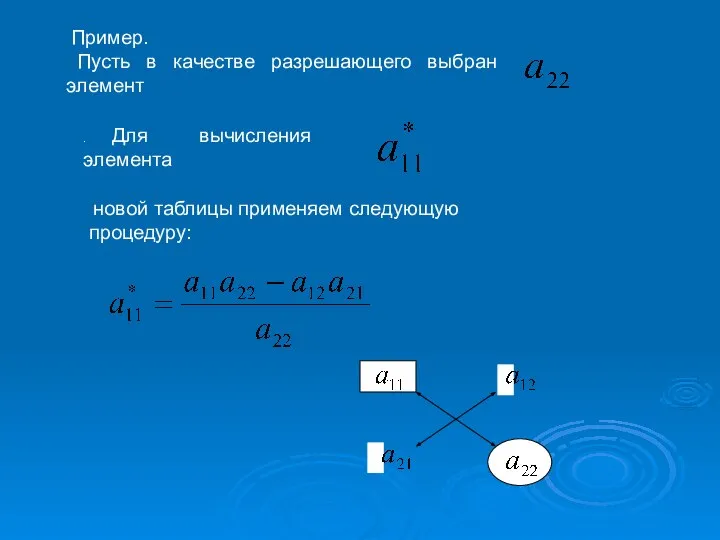
- 15. Пример. Пусть в качестве разрешающего выбран элемент . Для вычисления элемента новой таблицы применяем следующую процедуру:
- 16. Общая формулировка «правила прямоугольника» Из строк и столбцов разрешающего элемента и пересчитываемого элемента формируем прямоугольник; Из
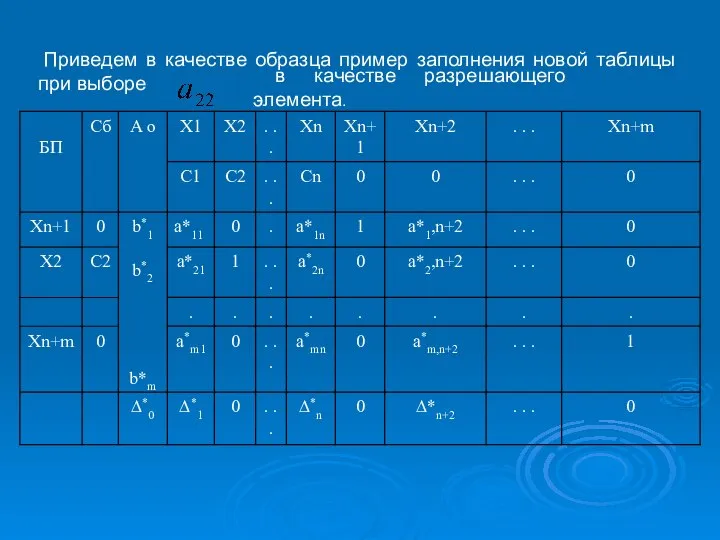
- 17. Приведем в качестве образца пример заполнения новой таблицы при выборе в качестве разрешающего элемента.
- 18. Если в результате преобразований все оценки индексной строки оказались неотрицательны при решении на max (или неположительны
- 19. Симплекс-метод с искусственным базисом Применяется при решении задач, у которых получение исходного неотрицательного базисного решения сопряжено
- 21. Скачать презентацию















 Пещерные храмы в Эллоре По теме: «Искусство Индии» Составила: учитель МХК МОУ СОШ № 131 г. Уссурийска Коляда Наталья Ивановна
Пещерные храмы в Эллоре По теме: «Искусство Индии» Составила: учитель МХК МОУ СОШ № 131 г. Уссурийска Коляда Наталья Ивановна Праздник в начальной школе автор учитель начальных классов МОУ «СОШ № 9» Зиброва Н.И. « Я здоровье берегу, сам себе я помогу
Праздник в начальной школе автор учитель начальных классов МОУ «СОШ № 9» Зиброва Н.И. « Я здоровье берегу, сам себе я помогу Разработка электронного учебника по дисциплине «Микропроцессоры»
Разработка электронного учебника по дисциплине «Микропроцессоры» Судебно-медицинская травматология
Судебно-медицинская травматология Операционные системы: Синхронизация процессов
Операционные системы: Синхронизация процессов Алгоритмизация и программирование
Алгоритмизация и программирование Презентация Таможенно-тарифное регулирование
Презентация Таможенно-тарифное регулирование «Сделки. Виды сделок» _
«Сделки. Виды сделок» _ Презентация на тему Бунташный век история отечества
Презентация на тему Бунташный век история отечества 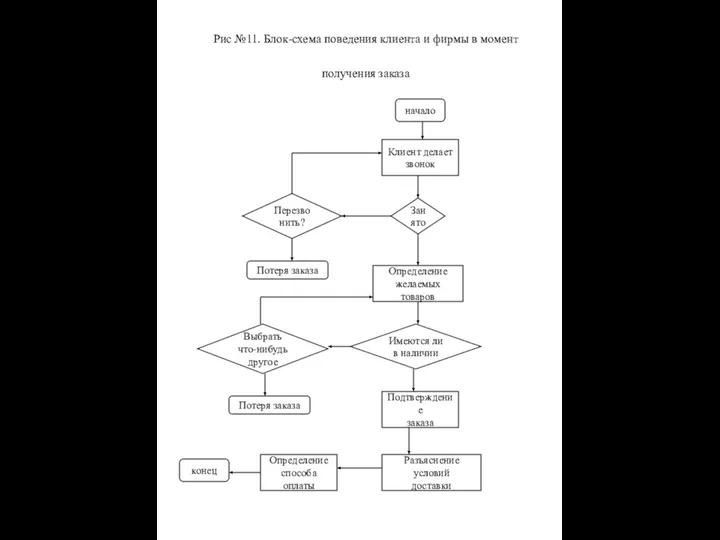 Блок-схема поведения клиента и фирмы в момент получения заказа
Блок-схема поведения клиента и фирмы в момент получения заказа Exercise Input-output-signals
Exercise Input-output-signals Строительная акустика. Звуковые волны. Спектры. Звуковое давление. Интенсивность звука
Строительная акустика. Звуковые волны. Спектры. Звуковое давление. Интенсивность звука Презентация "Истоки русской архитектуры" - скачать презентации по МХК
Презентация "Истоки русской архитектуры" - скачать презентации по МХК Осень в природе 2 часть - презентация для начальной школы_
Осень в природе 2 часть - презентация для начальной школы_ 25.05.2014 Итоговый педсовет «Результативность работы МБДОУ «ЦРР - детский сад «Теремок» за 2013-2014 учебный год
25.05.2014 Итоговый педсовет «Результативность работы МБДОУ «ЦРР - детский сад «Теремок» за 2013-2014 учебный год Створення Web-сторінок
Створення Web-сторінок Бальні танці
Бальні танці Музы древней Греции
Музы древней Греции Психологическая характеристика физических качеств
Психологическая характеристика физических качеств Иные участники уголовного судопроизводства
Иные участники уголовного судопроизводства  Теория строения органических соединений А.М. Бутлерова
Теория строения органических соединений А.М. Бутлерова  Пороки митрального клапана
Пороки митрального клапана Характеристика основных видов деятельности учителя по подготовке к уроку физической культуры
Характеристика основных видов деятельности учителя по подготовке к уроку физической культуры Единый урок безопасности в сети Интернет
Единый урок безопасности в сети Интернет Основы алгоритмизации и программирования на языках высокого уровня
Основы алгоритмизации и программирования на языках высокого уровня Фестивали, конкурсы 10.09. – 30.09.2012 проведение школьного этапа городского конкурса творческих работ старшеклассников «В чужих слов
Фестивали, конкурсы 10.09. – 30.09.2012 проведение школьного этапа городского конкурса творческих работ старшеклассников «В чужих слов Конструкторская документация. Виды соединений. Основные сведения о резьбе
Конструкторская документация. Виды соединений. Основные сведения о резьбе Проблемы психического развития в подростковый период (11 – 17 лет
Проблемы психического развития в подростковый период (11 – 17 лет