Содержание
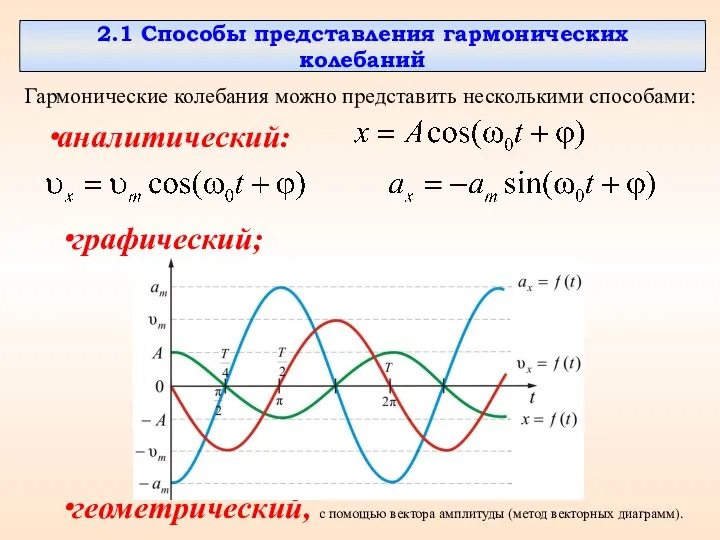
- 2. 2.1 Способы представления гармонических колебаний Гармонические колебания можно представить несколькими способами: аналитический: графический; геометрический, с помощью
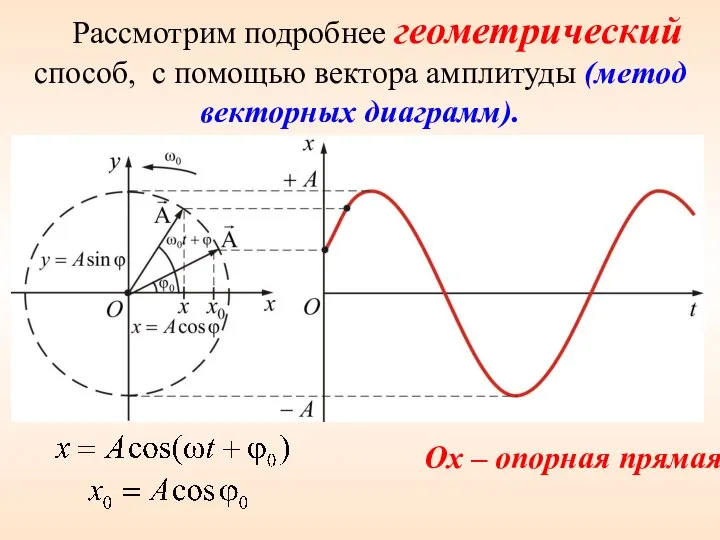
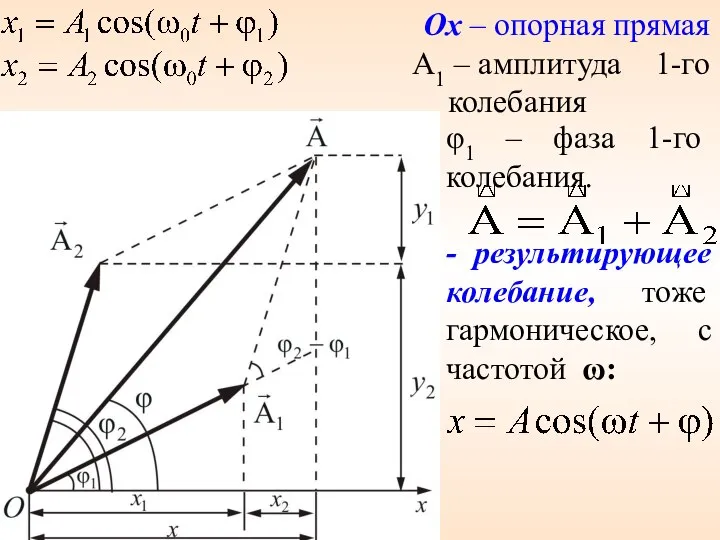
- 3. Рассмотрим подробнее геометрический способ, с помощью вектора амплитуды (метод векторных диаграмм). Ox – опорная прямая
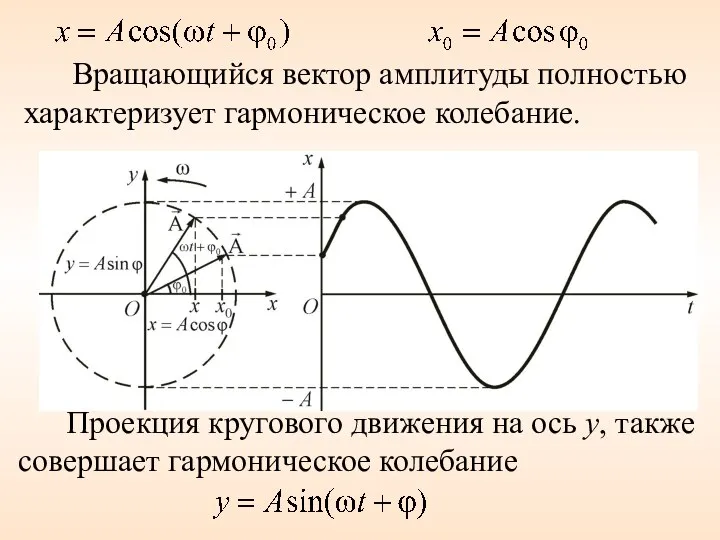
- 4. Вращающийся вектор амплитуды полностью характеризует гармоническое колебание. Проекция кругового движения на ось у, также совершает гармоническое
- 5. 2.2 Сложение гармонических колебаний. Биения Круговая волна на поверхности жидкости, возбуждаемая гармонически колеблющимся шариком. Интерференция между
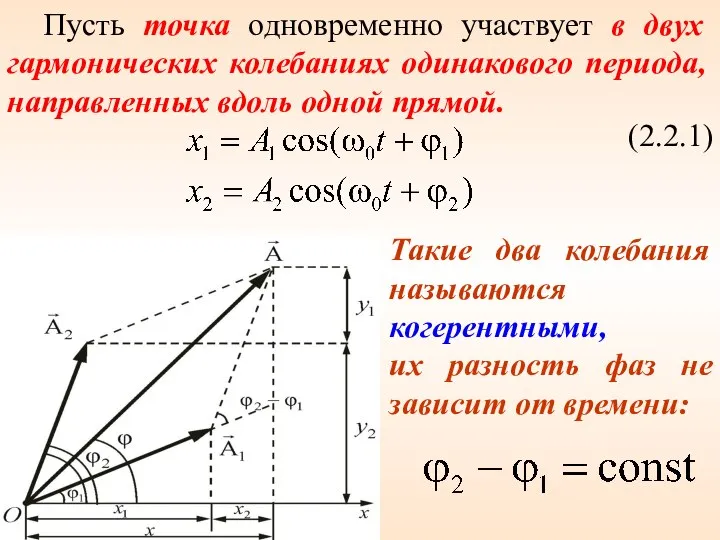
- 6. Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой. (2.2.1) Такие
- 7. Ox – опорная прямая A1 – амплитуда 1-го колебания φ1 – фаза 1-го колебания. - результирующее
- 8. По правилу сложения векторов найдем суммарную амплитуду, результирующего колебания: (2.2.2) Начальная фаза определяется из соотношения (2.2.3)
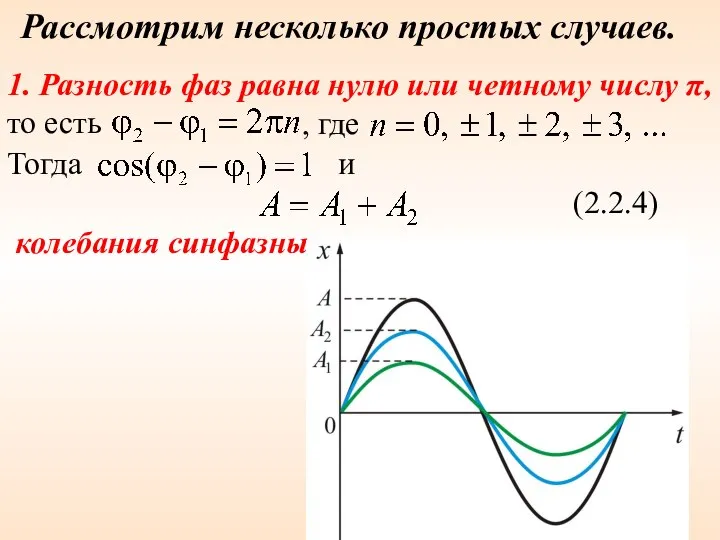
- 9. Рассмотрим несколько простых случаев. 1. Разность фаз равна нулю или четному числу π, то есть ,
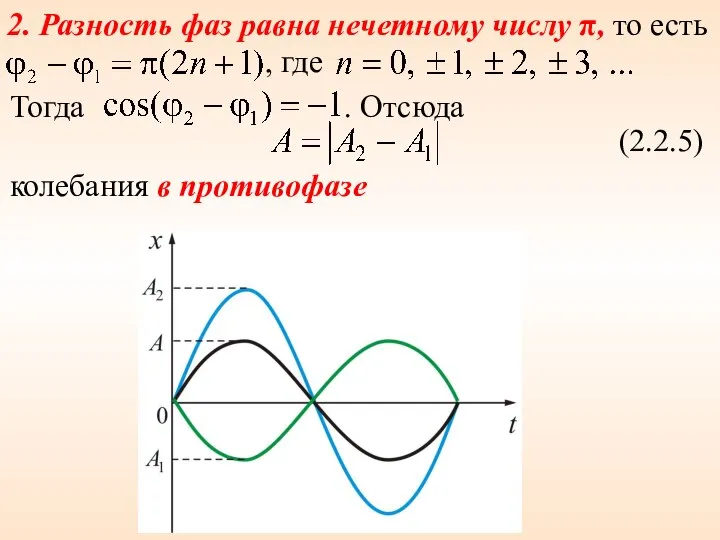
- 10. 2. Разность фаз равна нечетному числу π, то есть , где Тогда . Отсюда (2.2.5) колебания
- 11. 3. Разность фаз изменяется во времени произвольным образом (2.2.6) Это некогерентные колебания Здесь интересен случай, называемый
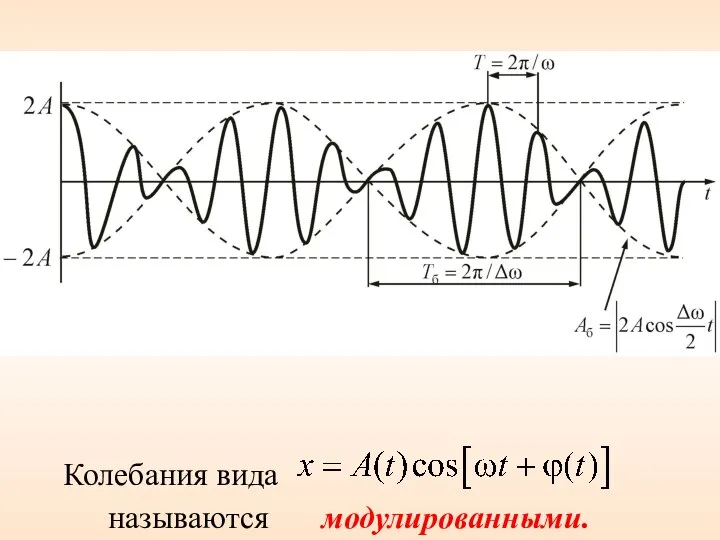
- 12. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами , называются биениями.
- 13. Колебания вида модулированными. называются
- 14. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д.
- 15. Слагаемые ряда Фурье, определяющие гармонические колебания с частотами ω, 2ω, 3ω, ..., называются первой (или основной),
- 16. 2.3 Сложение взаимно перпендикулярных колебаний ; (2.3.1) В результате получили уравнение эллипса с произвольно расположенными осями
- 17. 2.4 Фигуры Лиссажу (частные случаи) 1. Начальные фазы колебаний одинаковы (2.4.1) Это уравнение прямой, проходящей через
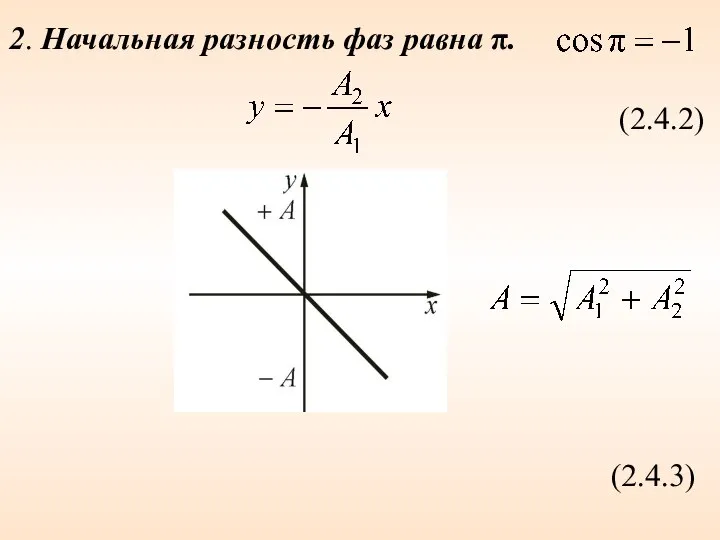
- 18. 2. Начальная разность фаз равна π. (2.4.2) (2.4.3)
- 19. 3. Начальная разность фаз равна π/2. (2.4.4) ( Эллиптически поляризованные колебания) При (циркулярно-поляризованные колебания). – получим
- 20. 4. Все остальные разности фаз дают эллипсы с различным углом наклона относительно осей координат. Фигуры, получаемые
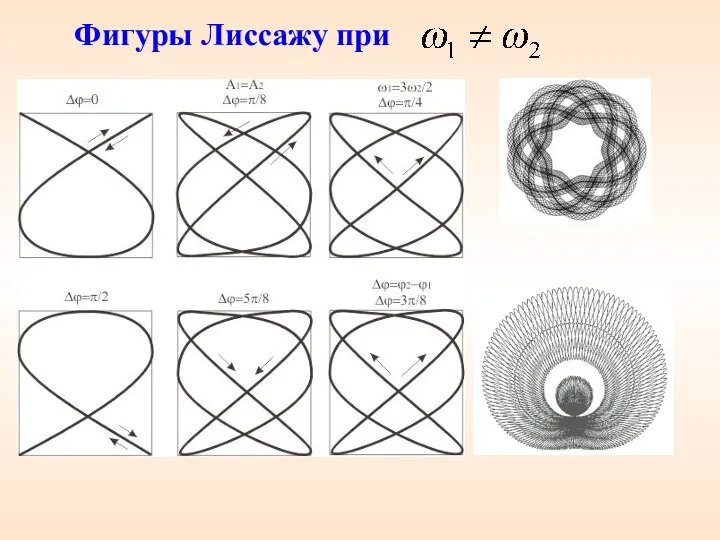
- 23. Фигуры Лиссажу при
- 25. Скачать презентацию












 Кыргыстан в составе России
Кыргыстан в составе России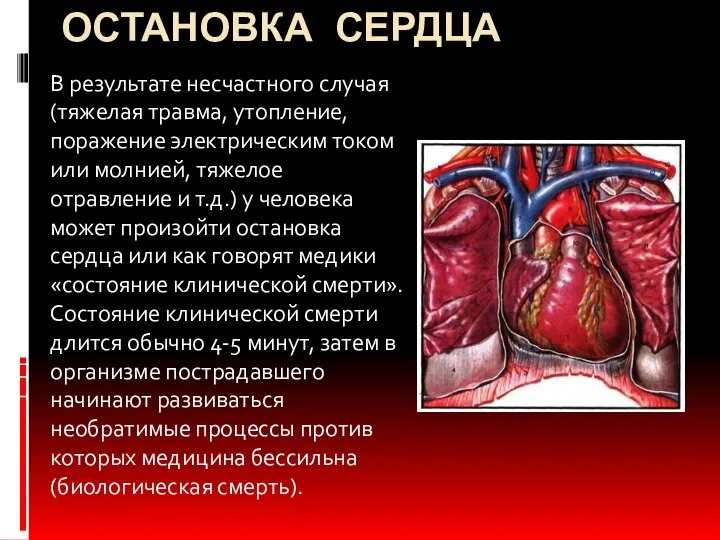 Остановка сердца В результате несчастного случая (тяжелая травма, утопление, поражение электрическим током или молнией, тяжелое о
Остановка сердца В результате несчастного случая (тяжелая травма, утопление, поражение электрическим током или молнией, тяжелое о Роль фармакотерапии в современной медицине и применение лекарственных средств
Роль фармакотерапии в современной медицине и применение лекарственных средств Проблемы и перспективы измерения эффективности маркетинга в Украине
Проблемы и перспективы измерения эффективности маркетинга в Украине  Религиозные конфликты
Религиозные конфликты Программирование. Базовый курс 2 часть
Программирование. Базовый курс 2 часть Общественно -политические движения Выполнили: Карпенко Т., Галибина Л., гр.Т-114 _
Общественно -политические движения Выполнили: Карпенко Т., Галибина Л., гр.Т-114 _ Василий Андреевич Тропинин 19 (30) марта 1776
Василий Андреевич Тропинин 19 (30) марта 1776  Тема 5 Современные теории международной торговли
Тема 5 Современные теории международной торговли Образование через всю жизнь
Образование через всю жизнь Стилистика, как наука
Стилистика, как наука Календари религий мира. Праздники в религиях мира
Календари религий мира. Праздники в религиях мира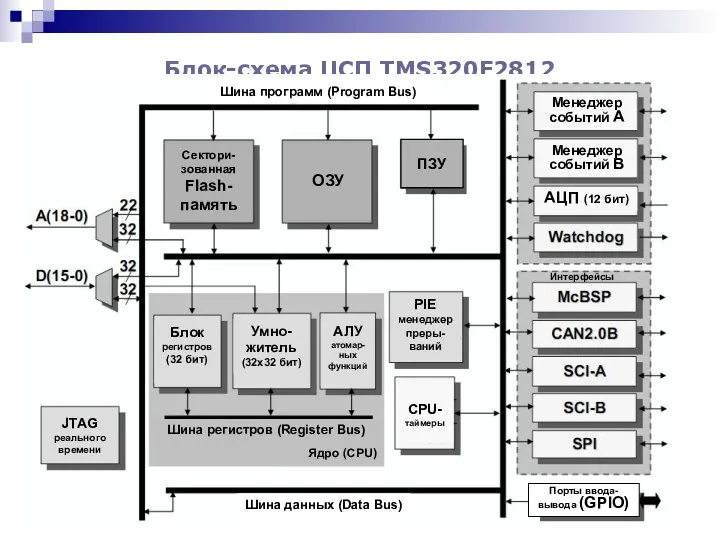 Блок-схема ЦСП TMS320F2812
Блок-схема ЦСП TMS320F2812 Памятники Индии, Японии, Китая
Памятники Индии, Японии, Китая Брак
Брак Презентация на тему "Формирование инновационной инфраструктуры внедрения научно-технической продукции в медицину" - скачать
Презентация на тему "Формирование инновационной инфраструктуры внедрения научно-технической продукции в медицину" - скачать ИНФОРМАЦИЯ ДЛЯ ПОТРЕБИТЕЛЯ
ИНФОРМАЦИЯ ДЛЯ ПОТРЕБИТЕЛЯ  ADO.NET. Технологии доступа к данным ADO.NET. (Лекция 20)
ADO.NET. Технологии доступа к данным ADO.NET. (Лекция 20) Административная школа управления
Административная школа управления  Организация программ циклической структуры. Массивы (регулярные типы)
Организация программ циклической структуры. Массивы (регулярные типы) Историческое время зарождения таможенного дела на Руси Основные предпосылки Тетеркина Кристина, ФТД, 1 курс, 1 пото
Историческое время зарождения таможенного дела на Руси Основные предпосылки Тетеркина Кристина, ФТД, 1 курс, 1 пото Анализ социальных результатов
Анализ социальных результатов  Semiconductor technology
Semiconductor technology Новый год в Италии
Новый год в Италии Презентация Классификация и организационные формы доходов бюджета государства
Презентация Классификация и организационные формы доходов бюджета государства Christmas tree
Christmas tree Задание прямой линии на чертеже
Задание прямой линии на чертеже Техника безопасности и правила поведения детей во время зимних каникул - презентация для начальной школы
Техника безопасности и правила поведения детей во время зимних каникул - презентация для начальной школы