Содержание
- 2. Результаты обучения. В результате изучения материала главы 12 учащийся должен: знать определение математического ожидания конечной случайной
- 3. П.53. Математическое ожидание случайной величины. Для введения понятия «математическое ожидание случайной величины» необходимо разобрать задачу п.53.
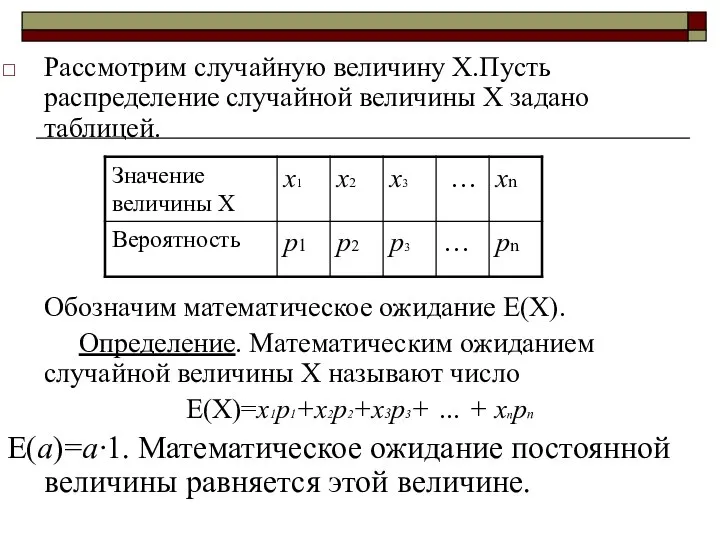
- 4. Рассмотрим случайную величину Х.Пусть распределение случайной величины Х задано таблицей. Обозначим математическое ожидание Е(Х). Определение. Математическим
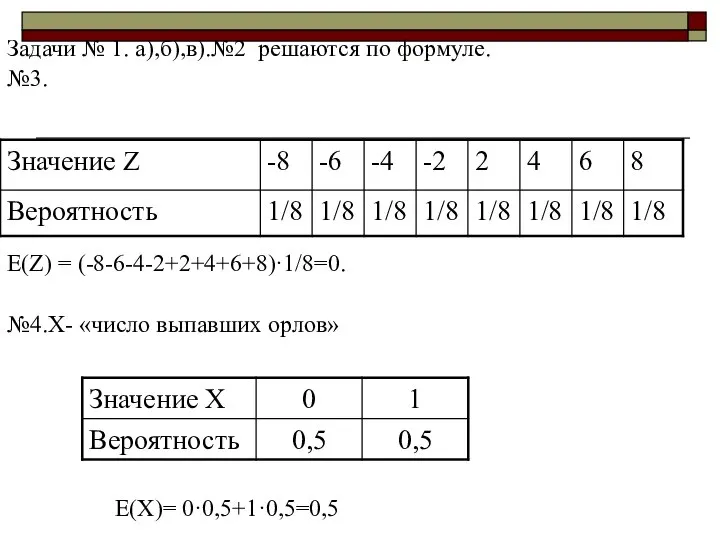
- 5. Задачи № 1. а),б),в).№2 решаются по формуле. №3. Е(Z) = (-8-6-4-2+2+4+6+8)·1/8=0. №4.Х- «число выпавших орлов» Е(Х)=
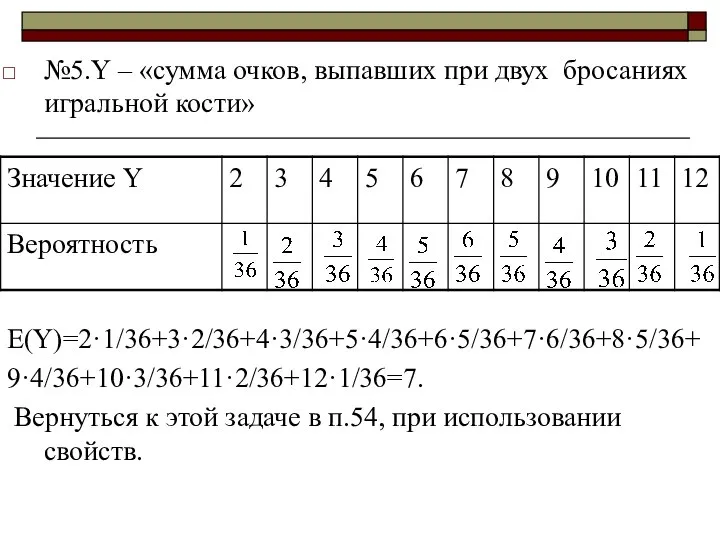
- 6. №5.Y – «сумма очков, выпавших при двух бросаниях игральной кости» Е(Y)=2·1/36+3·2/36+4·3/36+5·4/36+6·5/36+7·6/36+8·5/36+ 9·4/36+10·3/36+11·2/36+12·1/36=7. Вернуться к этой задаче
- 7. Задача № 9. Х – «число клеток в подбитом корабле» Е(Х)=0·0,8 +1·0,04 +2·0,06 +3·0,06+4·0,04 = 0,5.
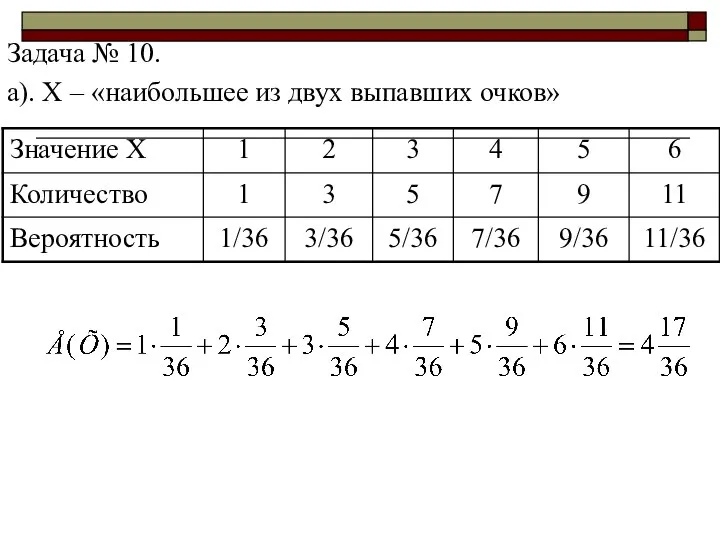
- 8. Задача № 10. а). Х – «наибольшее из двух выпавших очков»
- 9. №10 (б). Х – «наименьшее из двух выпавших очков»
- 10. П. 54. Свойства математического ожидания Свойство1.Пусть Х – случайная величина, а – некоторое число. Рассмотрим случайную
- 11. Задача № 1. Х – «число очков, выпавших на одной игральной кости» Е(Х) = 3,5 Тогда
- 12. Задача № 3. р=1/11. Е(Х) = 1/11·(-3-2-1+0+1+2+3+4+5+6+7)=2 р = 1/9. Е(Y)= 1/9·(1+2+3+4+5+6+7+8+9) = 5 a). Z=X+Y,
- 13. Задача № 5. Т.к. бросаний 5, то всего событий 32. Х – «выпадение орлов» Е(Х)=1/32·(0+ 1·5+2·10+3·10+4·5+5·1)=
- 14. П.56- 57. Дисперсия и стандартное отклонение. Свойства дисперсии. Дисперсия - мера рассеивания.(п.55) Дисперсией случайной величины Х
- 15. Задача № 2. Проводится одно испытание Бернулли, с вероятностью успеха р. Случайная величина S – «число
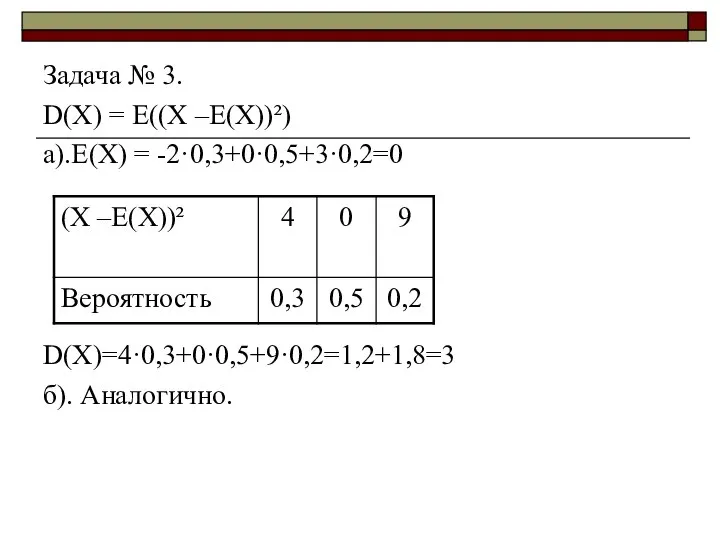
- 16. Задача № 3. D(X) = E((Х –Е(Х))²) а).Е(Х) = -2·0,3+0·0,5+3·0,2=0 D(X)=4·0,3+0·0,5+9·0,2=1,2+1,8=3 б). Аналогично.
- 17. Задача №4.б). Вычислить дисперсию случайной величины Х. D(X) = E((Х –Е(Х))²) Е(Х) = 3 Е((Х-Е(Х))²) =
- 18. Задача № 7. а). Случайная величина Х принимает значения от 0 до 6 с равными вероятностями,
- 19. Задача № 8. При решении используются свойства дисперсии. a). D(X) = 3, Y=3X, D(Y)= 9D(X), D(Y)=27
- 20. П. 58. Математическое ожидание числа успехов в серии испытаний Бернулли Если S – число успехов в
- 21. Задача № 1. 2000 – окуней и 1000 – карасей. Всего 3000 рыб. Найти ожидаемое число
- 22. Задача № 3. n=120 а).S – «число очков кратно 3» При бросании игральной кости с равной
- 23. Задача № 4. Вероятность успеха 0,25. Следовательно Е(S)=16·0.25=4. Т.е. ожидаемое число правильных ответов 4. Задача №5.
- 24. П. 59. Дисперсия числа успехов. Дисперсия числа успехов S в серии испытаний Бернулли вычисляется по формуле
- 25. Задача № 1. n = 100 p = 0,36, следовательно q = 0,64. D(S) = 0,36·0,64·100
- 26. Задача № 3. S – число попаданий серии выстрелов по мишени. р – вероятность попадания (вероятность
- 28. Скачать презентацию




















 Машина неделя - презентация для начальной школы
Машина неделя - презентация для начальной школы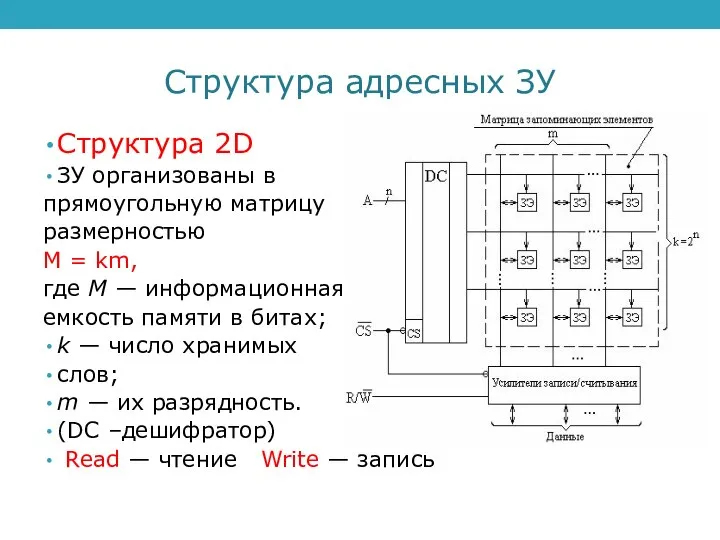 Структура адресных ЗУ
Структура адресных ЗУ Натюрморт в живописи
Натюрморт в живописи  Презентация на тему МЫШЕЧНАЯ ДЕЯТЕЛЬНОСТЬ.
Презентация на тему МЫШЕЧНАЯ ДЕЯТЕЛЬНОСТЬ.  Тема 8. Бюджетная политика
Тема 8. Бюджетная политика Среда программирования OpenMP. (Лекция 1)
Среда программирования OpenMP. (Лекция 1) Функції рекламного менеджменту
Функції рекламного менеджменту Презентация по толерантности
Презентация по толерантности Физическая культура. Футбол
Физическая культура. Футбол Учет труда и заработной платы. Выполнили: студенты группы ФТД-2 группы Т-093 Воробьев Д.Н. и Сушкова М.В.
Учет труда и заработной платы. Выполнили: студенты группы ФТД-2 группы Т-093 Воробьев Д.Н. и Сушкова М.В. Как жить в мире с родителями? Классный час
Как жить в мире с родителями? Классный час Asynchronous Transfer Mode Обзор технологии
Asynchronous Transfer Mode Обзор технологии Обьекты культного и природного всемирного наследия юнеско в Швейцарии
Обьекты культного и природного всемирного наследия юнеско в Швейцарии Автоматическая система теплопотребления и погодного регулирования в ИТП. Элеватор АРТФ и насос
Автоматическая система теплопотребления и погодного регулирования в ИТП. Элеватор АРТФ и насос Электрофизиологические основы электрокардиографии
Электрофизиологические основы электрокардиографии Муниципальные выборы: понятие, принципы, стадии избирательного процесса
Муниципальные выборы: понятие, принципы, стадии избирательного процесса Технология полного усвоения знаний В основе психолого-дидактическая концепция Дж. Керолла и Б. Блума
Технология полного усвоения знаний В основе психолого-дидактическая концепция Дж. Керолла и Б. Блума 12/2011 22.08-11.09 Учиться...Учиться?...Учиться!!! СНОВА В ШКОЛУ!... в школу КРАСОТЫ. - презентация_
12/2011 22.08-11.09 Учиться...Учиться?...Учиться!!! СНОВА В ШКОЛУ!... в школу КРАСОТЫ. - презентация_ Жанры изобразительного искусства Пейзаж , натюрморт , портрет , бытовой жанр , исторический и батальный , анималистический.
Жанры изобразительного искусства Пейзаж , натюрморт , портрет , бытовой жанр , исторический и батальный , анималистический.  Архитектурный облик Древней Руси IX-XII века
Архитектурный облик Древней Руси IX-XII века  Презентация Социальная структура и социальная стратификация общества
Презентация Социальная структура и социальная стратификация общества Цифровой образовательный ресурс Цифровой образовательный ресурс «Профилактика жестокого обращения с детьми дошкольного в
Цифровой образовательный ресурс Цифровой образовательный ресурс «Профилактика жестокого обращения с детьми дошкольного в Тема: Путешествие по Москве. Московский Кремль. Урок окружающего мира по программе А. А. Плешакова «Мир вокруг нас». 2 класс. – М.: Пр
Тема: Путешествие по Москве. Московский Кремль. Урок окружающего мира по программе А. А. Плешакова «Мир вокруг нас». 2 класс. – М.: Пр Презентация "История шелководства" - скачать презентации по МХК
Презентация "История шелководства" - скачать презентации по МХК ДОБРОЕ УТРО!
ДОБРОЕ УТРО!  Роль международных организаций в современном мире
Роль международных организаций в современном мире Виды дизайна Выполнила ученица 11 Б класса Кокоулина Анастасия
Виды дизайна Выполнила ученица 11 Б класса Кокоулина Анастасия Основы Web-дизайна. Введение в сайтостроение
Основы Web-дизайна. Введение в сайтостроение