Содержание
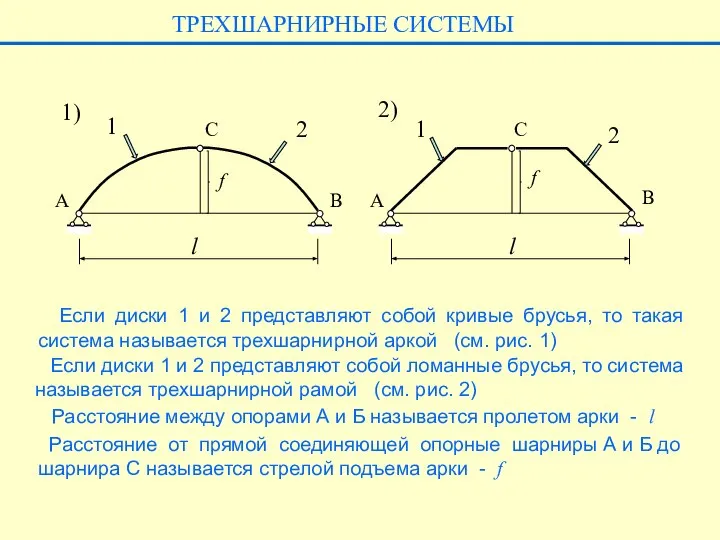
- 2. Если диски 1 и 2 представляют собой кривые брусья, то такая система называется трехшарнирной аркой (см.
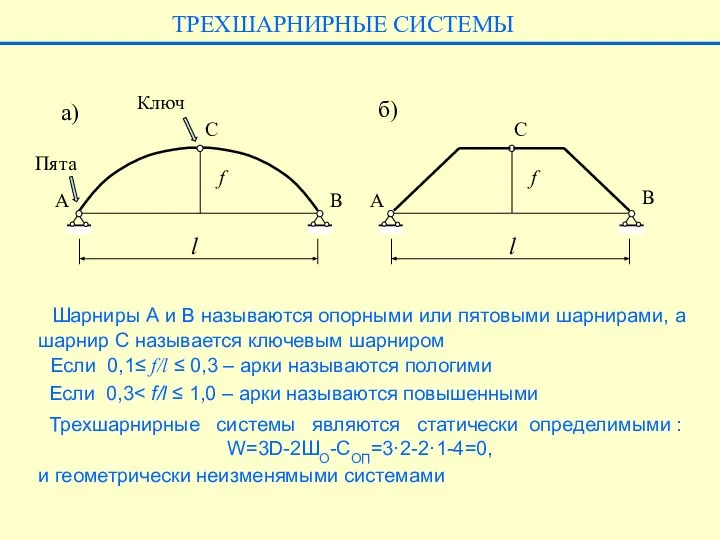
- 3. Шарниры А и В называются опорными или пятовыми шарнирами, а шарнир С называется ключевым шарниром ТРЕХШАРНИРНЫЕ
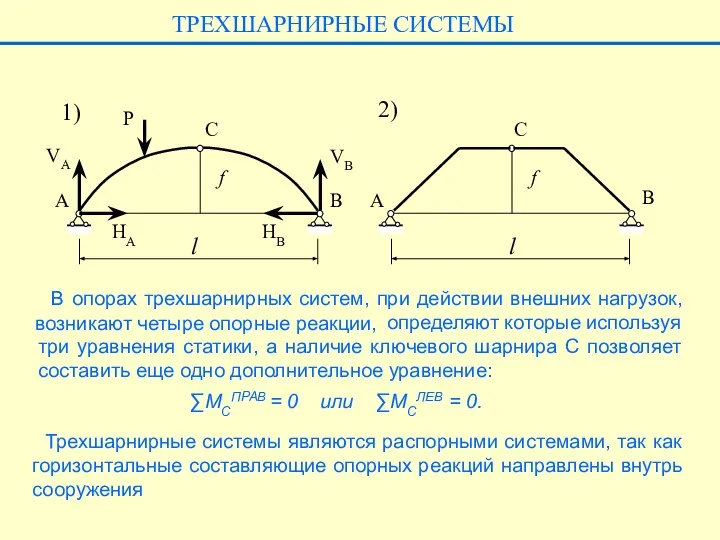
- 4. В опорах трехшарнирных систем, при действии внешних нагрузок, возникают четыре опорные реакции, ТРЕХШАРНИРНЫЕ СИСТЕМЫ A A
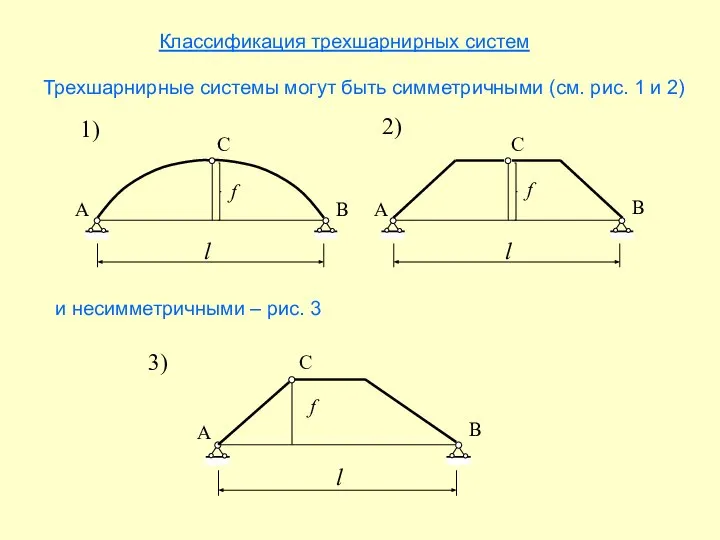
- 5. Классификация трехшарнирных систем Трехшарнирные системы могут быть симметричными (см. рис. 1 и 2) 3) и несимметричными
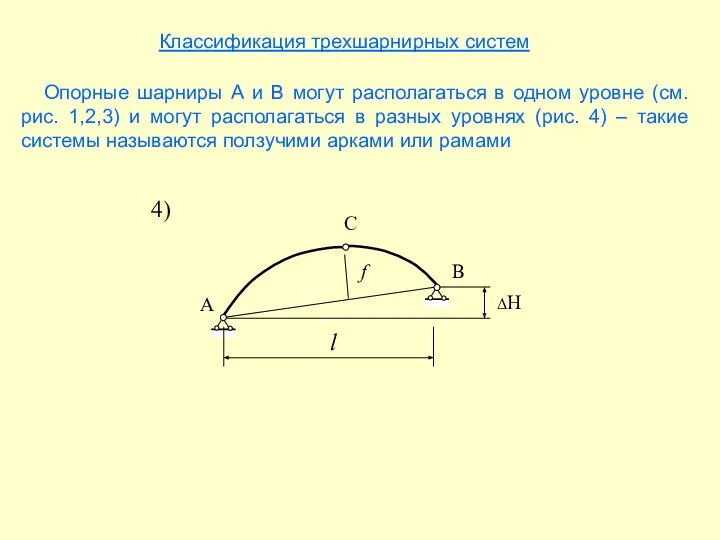
- 6. Классификация трехшарнирных систем Опорные шарниры А и В могут располагаться в одном уровне (см.рис. 1,2,3) и
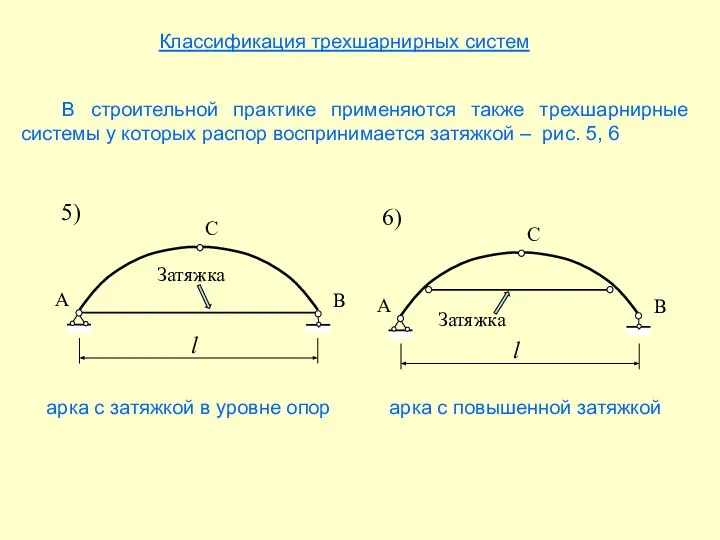
- 7. Классификация трехшарнирных систем В строительной практике применяются также трехшарнирные системы у которых распор воспринимается затяжкой –
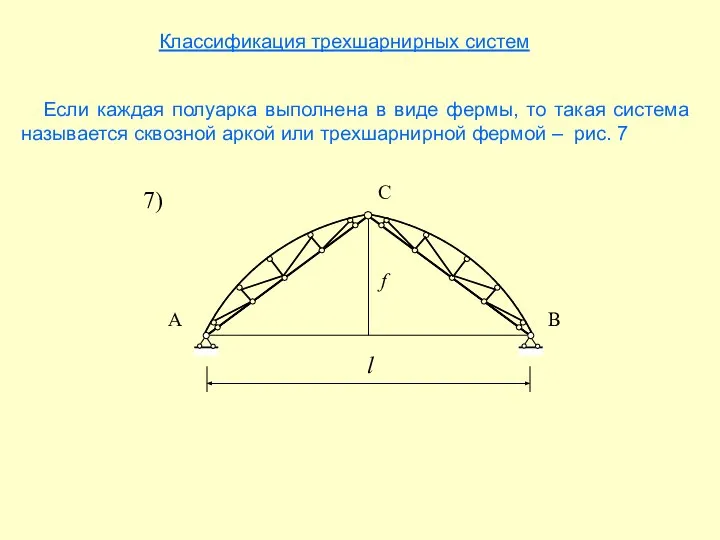
- 8. Классификация трехшарнирных систем Если каждая полуарка выполнена в виде фермы, то такая система называется сквозной аркой
- 9. Расчет трехшарнирных арок на неподвижные нагрузки C A B 1. Опорные реакции ∑МА=0; => VB =
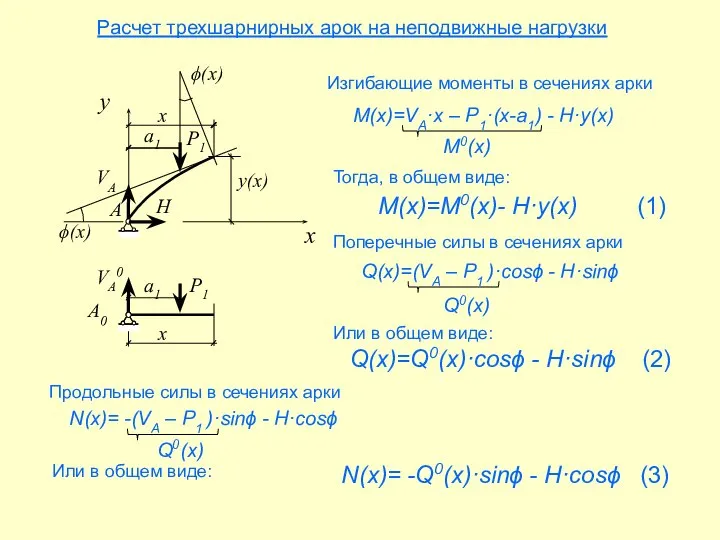
- 10. Расчет трехшарнирных арок на неподвижные нагрузки ϕ(x) Изгибающие моменты в сечениях арки M(x)=VA·x – P1·(x-a1) -
- 11. Для построения эпюр в трехшарнирных арках поступают следующим образом. По полученным значениям усилий строят соответствующие эпюры.
- 12. Вид эпюр и значения величин внутренних усилий в арках зависят от очертания оси арки. Такая арка
- 13. Арка рационального очертания C A B Уравнение (1) изгибающих моментов в сечениях арки записывается M(x)=M0(x)- H·y(x)
- 14. Арка рационального очертания M0(x)=(ql/2)⋅x – qx2/2 = (q/2)·x⋅(l - x) M0C = (ql)/2⋅l/2 - (ql)/2⋅l/4 =
- 15. Особенности расчета арок с затяжками 1. Рассмотрим арку с затяжкой в уровне опор При действии на
- 16. Особенности расчета арок с затяжками 1. Рассмотрим арку с затяжкой в уровне опор Внутренние усилия в
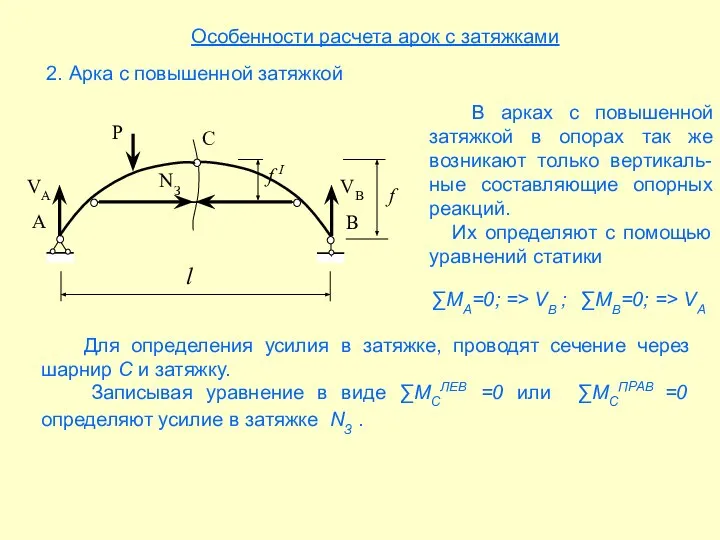
- 17. Особенности расчета арок с затяжками 2. Арка с повышенной затяжкой В арках с повышенной затяжкой в
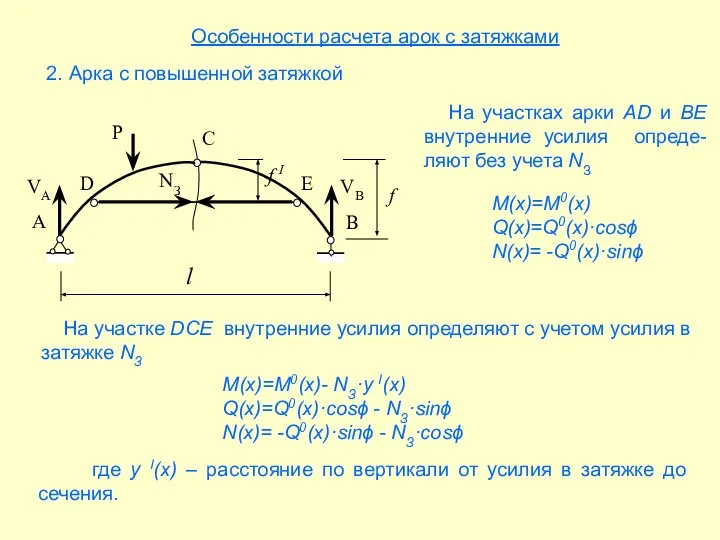
- 18. Особенности расчета арок с затяжками 2. Арка с повышенной затяжкой На участках арки AD и BЕ
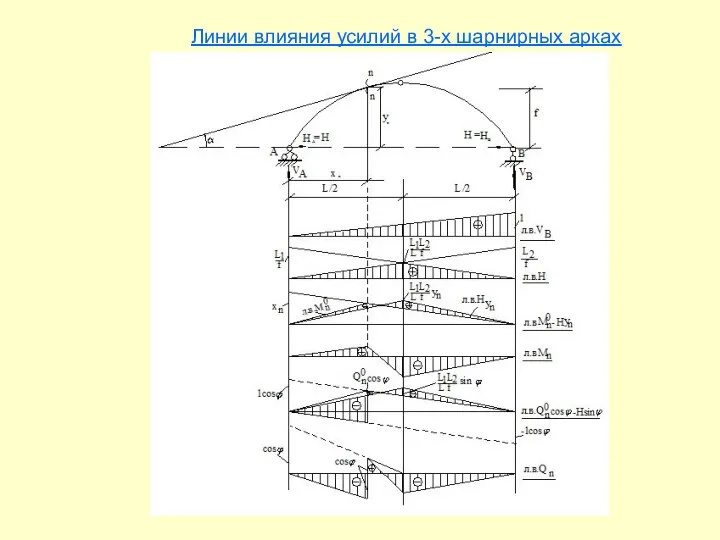
- 19. Линии влияния усилий в 3-х шарнирных арках
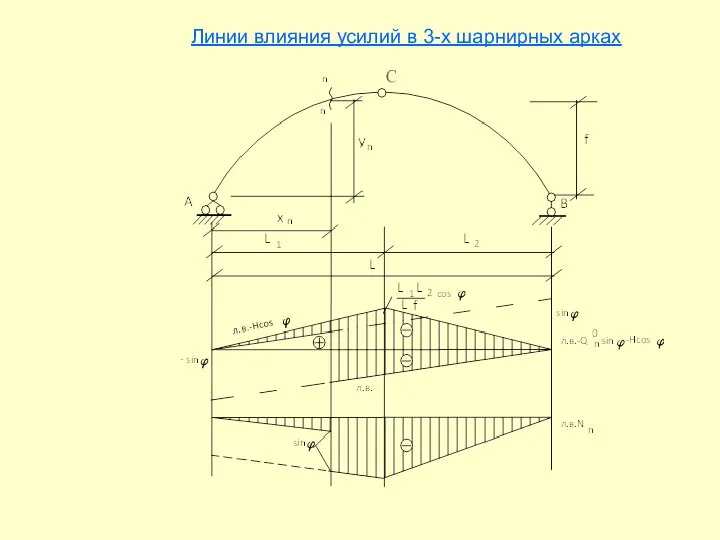
- 20. Линии влияния усилий в 3-х шарнирных арках
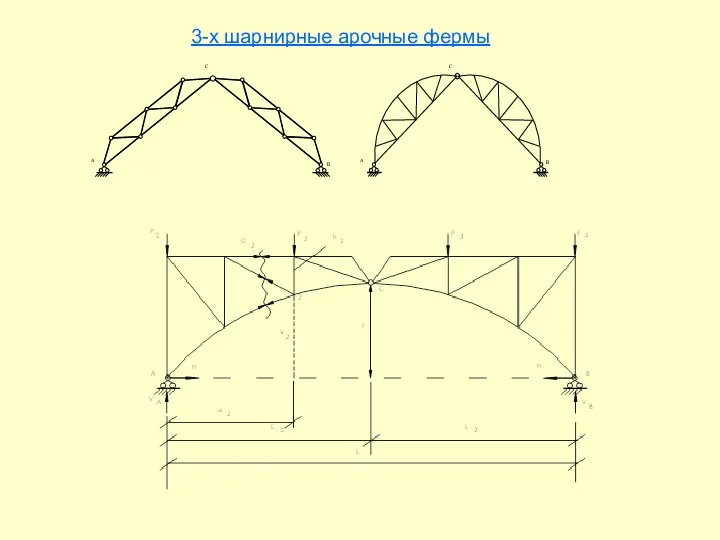
- 21. 3-х шарнирные арочные фермы
- 23. Скачать презентацию







 Кроссворд по экономической географии по теме Миграция
Кроссворд по экономической географии по теме Миграция Презентация основные принципы перемещения товаров и транспортных средств через таможенную границу
Презентация основные принципы перемещения товаров и транспортных средств через таможенную границу Определение войскового тыла
Определение войскового тыла Личностно-ориентированные технологии обучения
Личностно-ориентированные технологии обучения  Информационные системы в управлении
Информационные системы в управлении Игра Поле чудес - презентация для начальной школы
Игра Поле чудес - презентация для начальной школы «ХХІ ғасыр көшбасшысы» 5-сынып
«ХХІ ғасыр көшбасшысы» 5-сынып Условная трансляция Макрокоманды
Условная трансляция Макрокоманды  Презентация "Аромамаркетинг" - скачать презентации по Экономике
Презентация "Аромамаркетинг" - скачать презентации по Экономике Внутришкольный семинар Методы и формы работы с « трудными» детьми.
Внутришкольный семинар Методы и формы работы с « трудными» детьми. Зачем ребёнку кукольный театр? - презентация для начальной школы_
Зачем ребёнку кукольный театр? - презентация для начальной школы_ Социальные институты формирования отношения к здоровью
Социальные институты формирования отношения к здоровью «Первичная экологическая экспертиза упакованных продуктов» Научно- исследовательская работа в 4 «Б» классе. Работу выполнили: До
«Первичная экологическая экспертиза упакованных продуктов» Научно- исследовательская работа в 4 «Б» классе. Работу выполнили: До ВЕЛИКИЕ МАТЕМАТИКИ
ВЕЛИКИЕ МАТЕМАТИКИ  Презентация на тему "Федеральные государственные образовательные стандарты второго поколения" - скачать презентации по Педа
Презентация на тему "Федеральные государственные образовательные стандарты второго поколения" - скачать презентации по Педа газопламенное напыление
газопламенное напыление Понятие о четырехполюсниках и их классификация. Четырехполюсники и их основные уравнения.
Понятие о четырехполюсниках и их классификация. Четырехполюсники и их основные уравнения. Начертательная геометрия. Поверхности. (Лекция 4)
Начертательная геометрия. Поверхности. (Лекция 4) Сущность и виды административного процесса
Сущность и виды административного процесса ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ (5 итоговый урок)
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ (5 итоговый урок) ГТО в 21 веке
ГТО в 21 веке Основы современного менеджмента в здравоохранении
Основы современного менеджмента в здравоохранении Суть багатокультурності і її проява в українському суспільсті. Етнічна, гендерна, конфесійна різноманітність. Рівність
Суть багатокультурності і її проява в українському суспільсті. Етнічна, гендерна, конфесійна різноманітність. Рівність Функции социально-культурной деятельности
Функции социально-культурной деятельности Сокращение таможен и внешней торговли России
Сокращение таможен и внешней торговли России Правовое регулирование трудоустройства и занятости
Правовое регулирование трудоустройства и занятости презентация для семинара Моя семейная история
презентация для семинара Моя семейная история Одяг часів НЕПу (1921-1928)
Одяг часів НЕПу (1921-1928)