Содержание
- 2. 2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ) 2.5. Выпуклые оболочки.
- 3. 2.5. Выпуклые оболочки. Определение 9. называется выпуклой комбинацией Теорема 9 Необходимость. Предположим, что утверждение теоремы верно
- 4. Полагаем Имеет место равенство С другой стороны
- 5. Необходимость доказана. Достаточность. Достаточность доказана. следовательно, оно выпукло. любых своих двух точек, Теорема 10. – фиксированные
- 6. Тогда для любых имеет место Кроме того Теорема доказана. Из доказанной теоремы легко выводится, например,
- 7. Упражнение. Решение.
- 8. По аналогии с аффинной оболочкой множества введем понятие выпуклой оболочки множества. Определение 10. Пересечение всех выпуклых
- 9. Доказательство. Теорема 11.
- 10. В качестве примера заметим, что выпуклая оболочка двух точек на плоскости представляет собой отрезок прямой, их
- 11. Согласно теореме 10 справедливо равенство Теорема 12 (Каратеодори). Доказательство. Покажем, что число слагаемых (ненулевых!) в этом
- 12. В силу (1) а их сумма равна нулю, и (2)
- 13. Теорема доказана.
- 15. Скачать презентацию












 Динамические и статистические закономерности, особенности их проявления
Динамические и статистические закономерности, особенности их проявления Нарушение функционирования рычага механизма переключения коробки передач
Нарушение функционирования рычага механизма переключения коробки передач Методы фиксации цен во внешнеторговых контрактах
Методы фиксации цен во внешнеторговых контрактах Реалистические тенденции в живописи Голландии. Тема 4 Автор: учитель истории Привалова В.С.
Реалистические тенденции в живописи Голландии. Тема 4 Автор: учитель истории Привалова В.С. Закономерности истории политики. (Тема 4)
Закономерности истории политики. (Тема 4) политика монетизации экономика Давлатзода П С Группа Т-093
политика монетизации экономика Давлатзода П С Группа Т-093 Государственные награды РФ
Государственные награды РФ Махамбет Өтемісұлы (1803 – 1846 )
Махамбет Өтемісұлы (1803 – 1846 ) Сжатие данных
Сжатие данных  Презентация "Факторинг" - скачать презентации по Экономике
Презентация "Факторинг" - скачать презентации по Экономике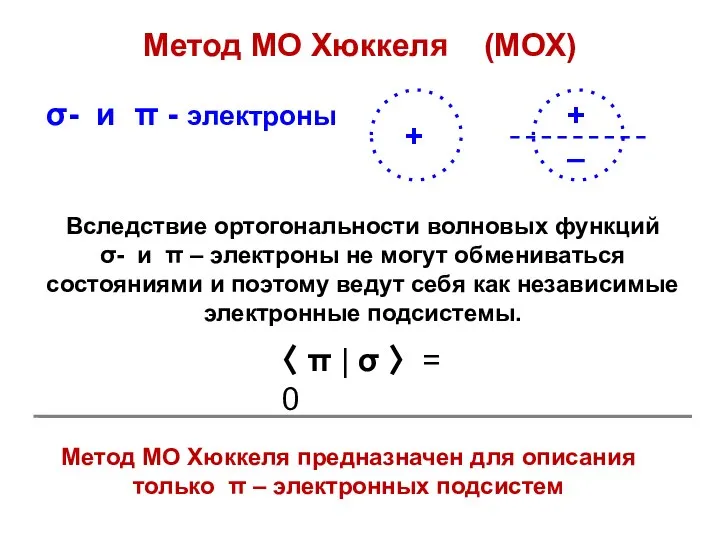 Метод Хюккеля
Метод Хюккеля Презентация "Золотые травы хохломы" - скачать презентации по МХК
Презентация "Золотые травы хохломы" - скачать презентации по МХК tragedia_Beslana
tragedia_Beslana Экономический портал Белгородской области при поддержке Аппарата губернатора Белгородской области предлагает Вам свои услуг
Экономический портал Белгородской области при поддержке Аппарата губернатора Белгородской области предлагает Вам свои услуг ТАЙМ-менеджмент Управление временем в бережливом производстве / офисе Семинар по бережливому производству
ТАЙМ-менеджмент Управление временем в бережливом производстве / офисе Семинар по бережливому производству  Морфологическая структура ландшафта
Морфологическая структура ландшафта Политическая система. Развитие теории политической системы
Политическая система. Развитие теории политической системы 7475
7475 Пресметни и посочи: /в случай че те затрудни, натисни/ 3 + 2 =
Пресметни и посочи: /в случай че те затрудни, натисни/ 3 + 2 = Индуистский храм
Индуистский храм Основные причины низкой эффективности оказания государственных (муниципальных) услуг
Основные причины низкой эффективности оказания государственных (муниципальных) услуг Презентация на тему: «Возникновение государства и права в Армении»
Презентация на тему: «Возникновение государства и права в Армении»  Германская фонология
Германская фонология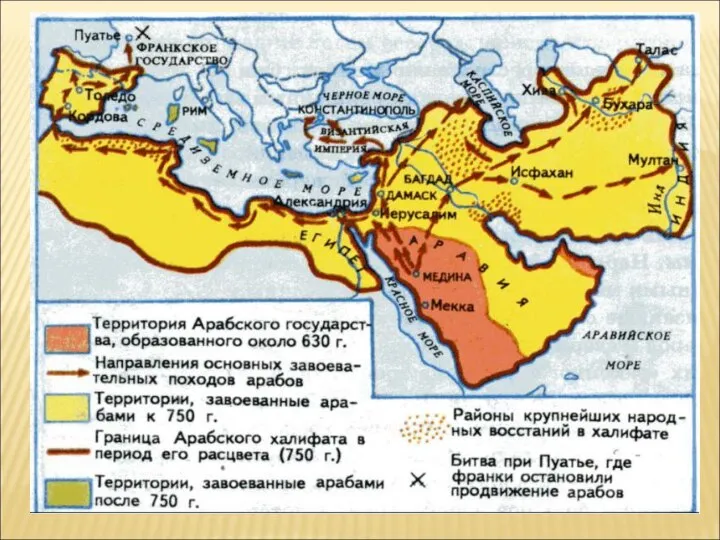 Культура стран халифата
Культура стран халифата СУБКУЛЬТУРЫ Субкультура (подкультура, лат. sub — под и лат. cultura — возделывание, земледелие, воспитание, почитание) в социологи
СУБКУЛЬТУРЫ Субкультура (подкультура, лат. sub — под и лат. cultura — возделывание, земледелие, воспитание, почитание) в социологи Крепежные детали. Резьбовые соединения
Крепежные детали. Резьбовые соединения ДелоБанк. Ролик для ТВ
ДелоБанк. Ролик для ТВ Город Киров на реке Вятка
Город Киров на реке Вятка