Содержание
- 2. Символика и обозначение
- 3. Предмет «Начертательная геометрия» Начертательная геометрия изучает пространственные формы и их отношения, используя метод проецирования с помощью
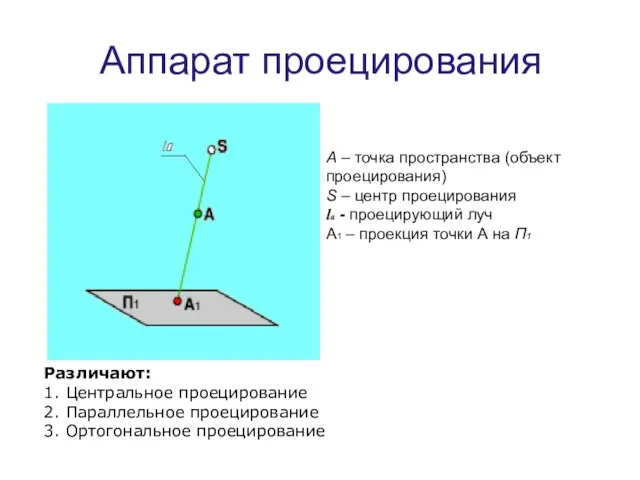
- 4. Аппарат проецирования А – точка пространства (объект проецирования) S – центр проецирования lа - проецирующий луч
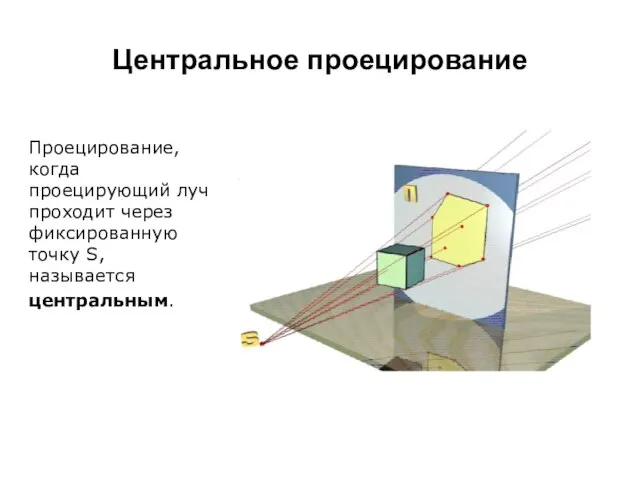
- 5. Центральное проецирование Проецирование, когда проецирующий луч проходит через фиксированную точку S, называется центральным.
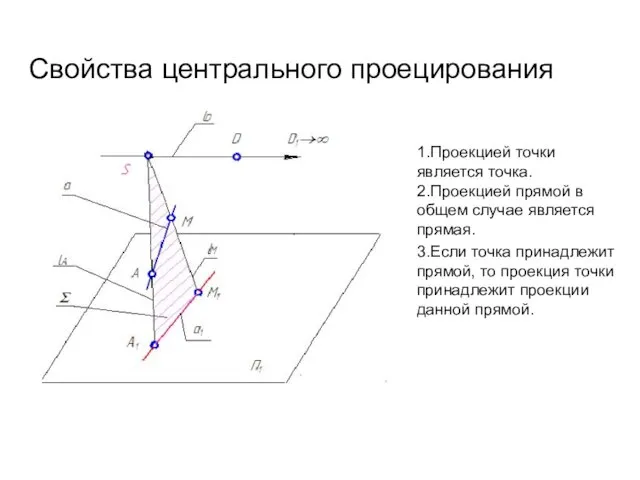
- 6. 1.Проекцией точки является точка. 2.Проекцией прямой в общем случае является прямая. 3.Если точка принадлежит прямой, то
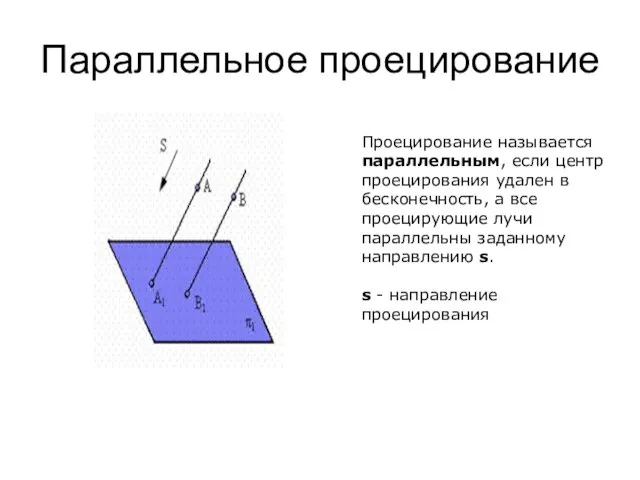
- 7. Параллельное проецирование Проецирование называется параллельным, если центр проецирования удален в бесконечность, а все проецирующие лучи параллельны
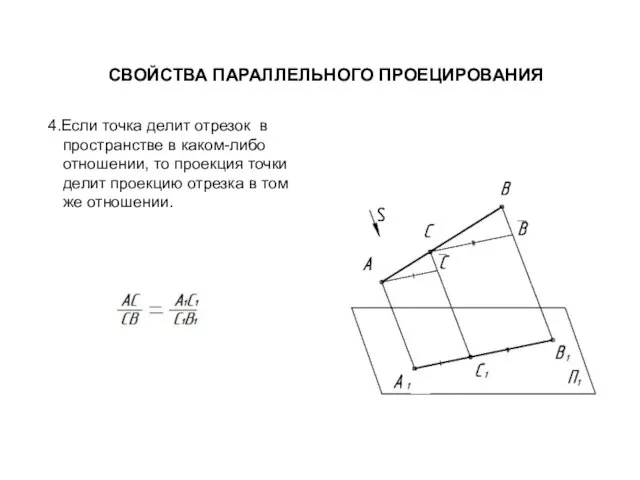
- 8. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ 4.Если точка делит отрезок в пространстве в каком-либо отношении, то проекция точки делит
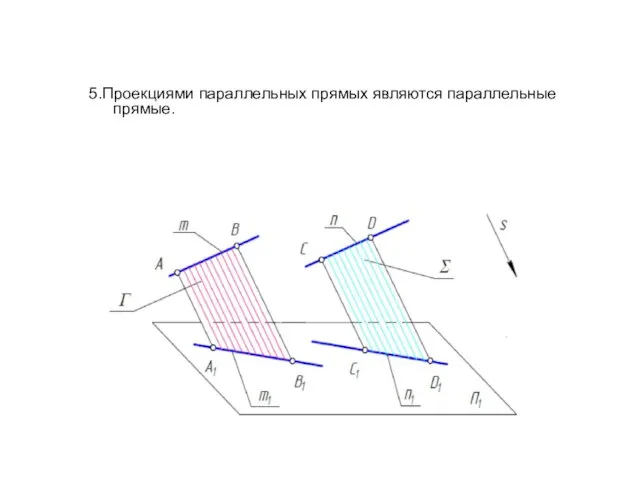
- 9. 5.Проекциями параллельных прямых являются параллельные прямые.
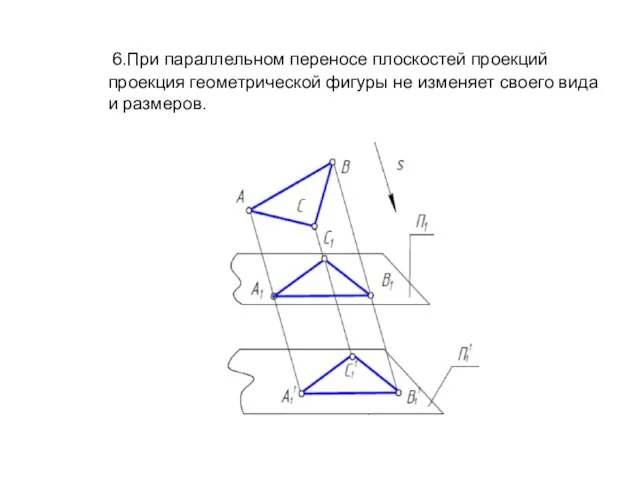
- 10. 6.При параллельном переносе плоскостей проекций проекция геометрической фигуры не изменяет своего вида и размеров.
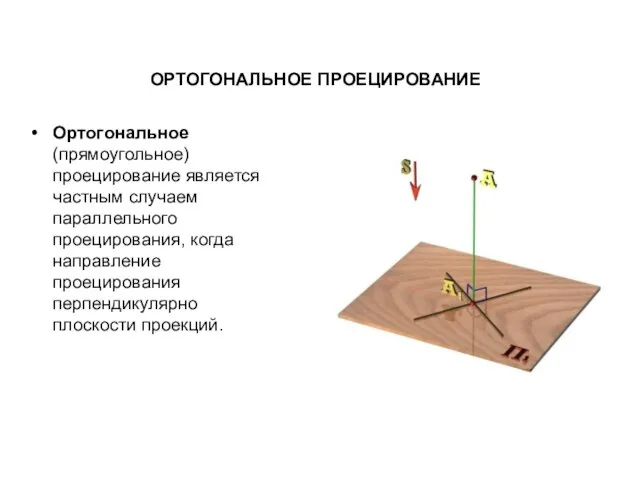
- 11. ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ Ортогональное (прямоугольное) проецирование является частным случаем параллельного проецирования, когда направление проецирования перпендикулярно плоскости проекций.
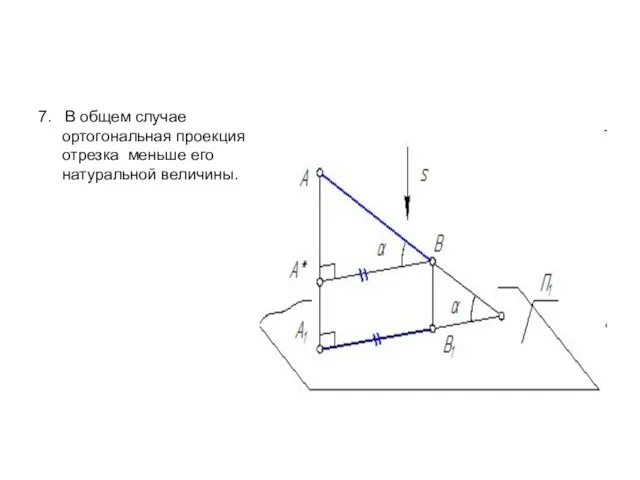
- 12. 7. В общем случае ортогональная проекция отрезка меньше его натуральной величины.
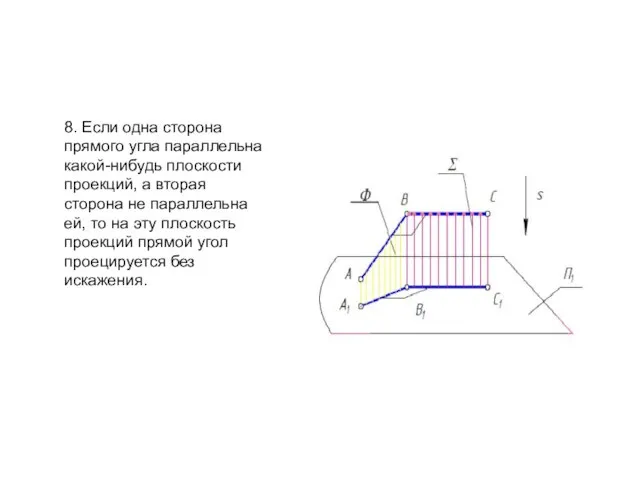
- 13. 8. Если одна сторона прямого угла параллельна какой-нибудь плоскости проекций, а вторая сторона не параллельна ей,
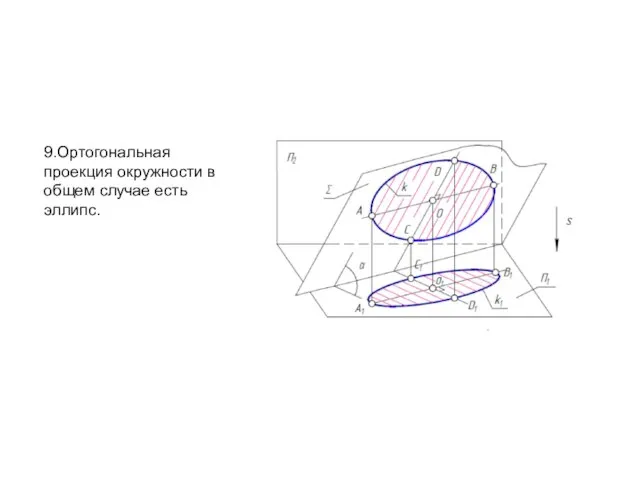
- 14. 9.Ортогональная проекция окружности в общем случае есть эллипс.
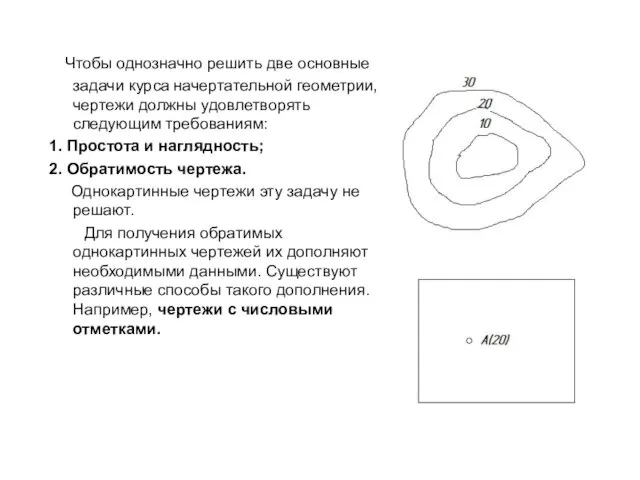
- 15. Чтобы однозначно решить две основные задачи курса начертательной геометрии, чертежи должны удовлетворять следующим требованиям: 1. Простота
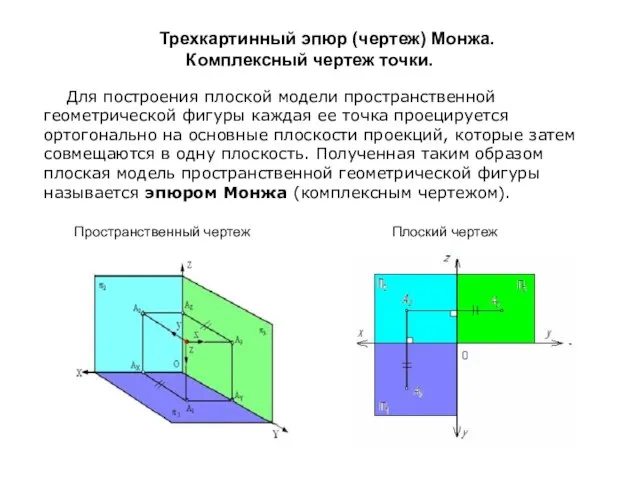
- 16. Трехкартинный эпюр (чертеж) Монжа. Комплексный чертеж точки. Пространственный чертеж Плоский чертеж Для построения плоской модели пространственной
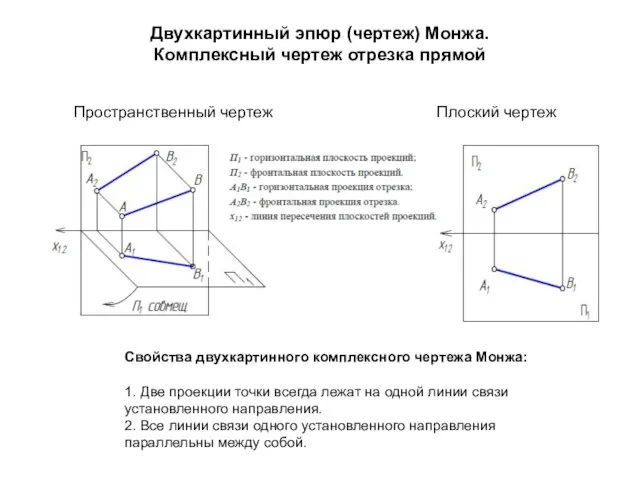
- 17. Двухкартинный эпюр (чертеж) Монжа. Комплексный чертеж отрезка прямой Пространственный чертеж Плоский чертеж Свойства двухкартинного комплексного чертежа
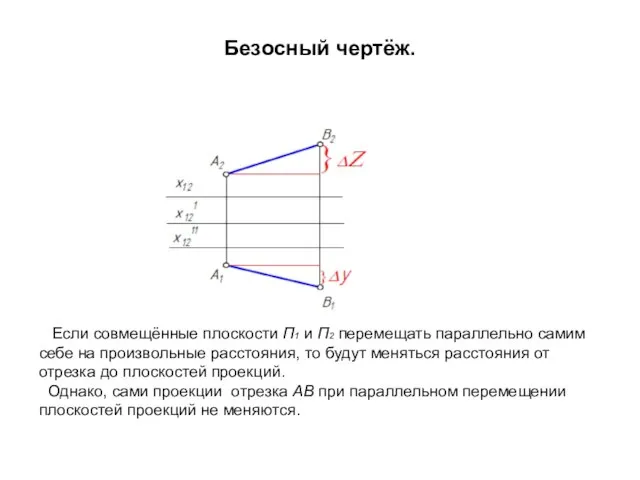
- 18. Безосный чертёж. Если совмещённые плоскости П1 и П2 перемещать параллельно самим себе на произвольные расстояния, то
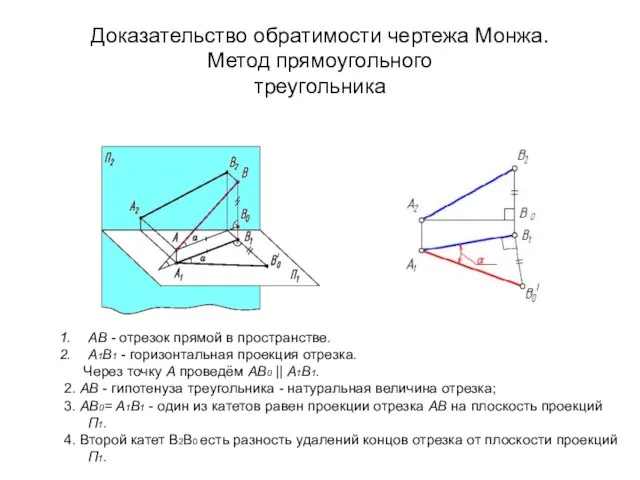
- 19. Доказательство обратимости чертежа Монжа. Метод прямоугольного треугольника AB - отрезок прямой в пространстве. A1B1 - горизонтальная
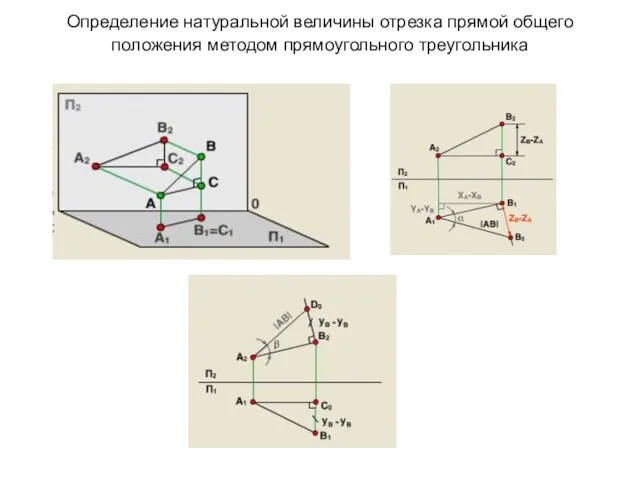
- 20. Определение натуральной величины отрезка прямой общего положения методом прямоугольного треугольника
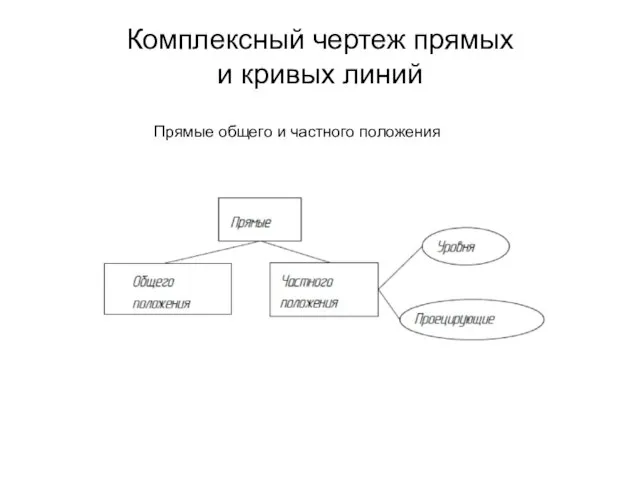
- 21. Комплексный чертеж прямых и кривых линий Прямые общего и частного положения
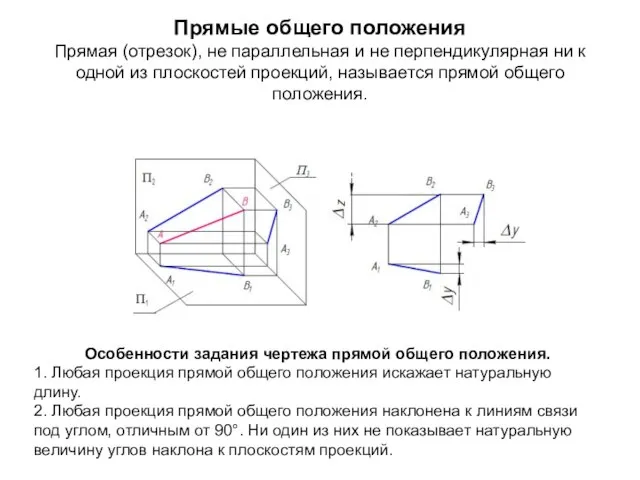
- 22. Прямые общего положения Прямая (отрезок), не параллельная и не перпендикулярная ни к одной из плоскостей проекций,
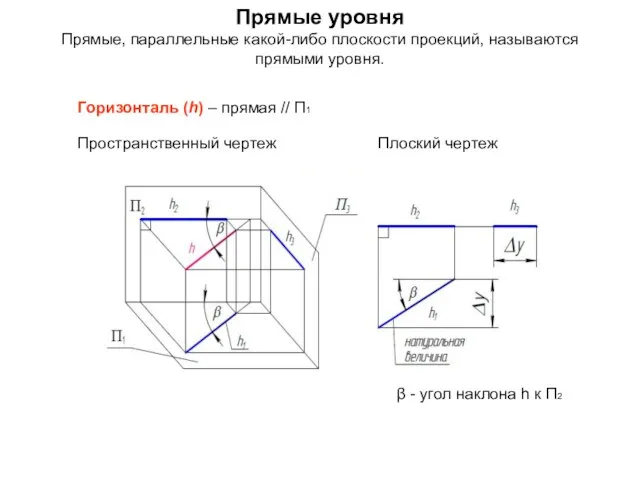
- 23. Прямые уровня Прямые, параллельные какой-либо плоскости проекций, называются прямыми уровня. Горизонталь (h) – прямая // П1
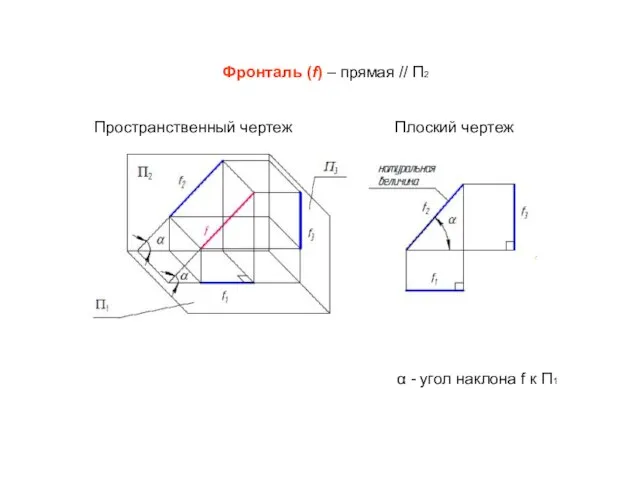
- 24. Фронталь (f) – прямая // П2 Пространственный чертеж Плоский чертеж α - угол наклона f к
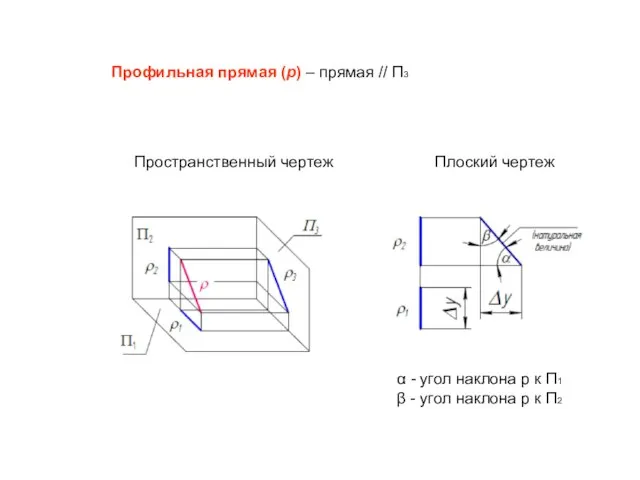
- 25. Пространственный чертеж Плоский чертеж Профильная прямая (p) – прямая // П3 α - угол наклона p
- 26. Особенности задания прямых уровня на комплексном чертеже 1. Одна из проекций прямых уровня перпендикулярна линиям связи
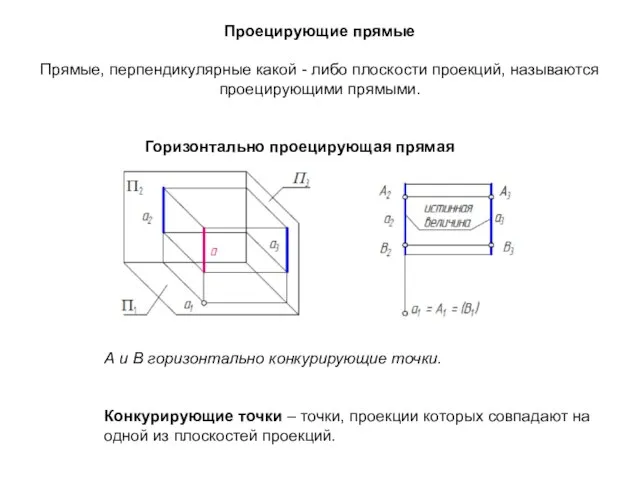
- 27. Проецирующие прямые Прямые, перпендикулярные какой - либо плоскости проекций, называются проецирующими прямыми. Горизонтально проецирующая прямая А
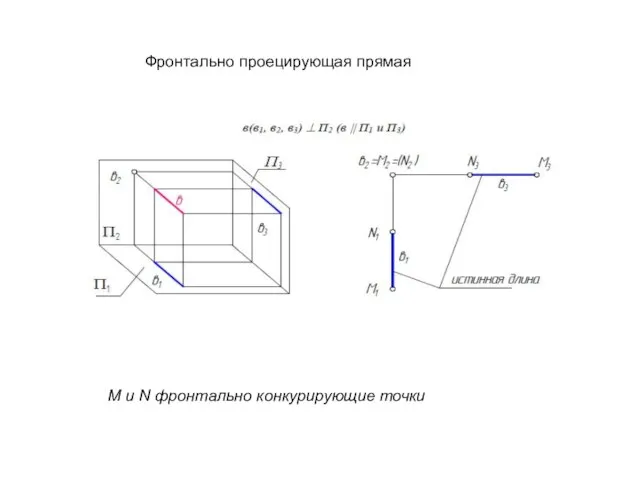
- 28. Фронтально проецирующая прямая М и N фронтально конкурирующие точки
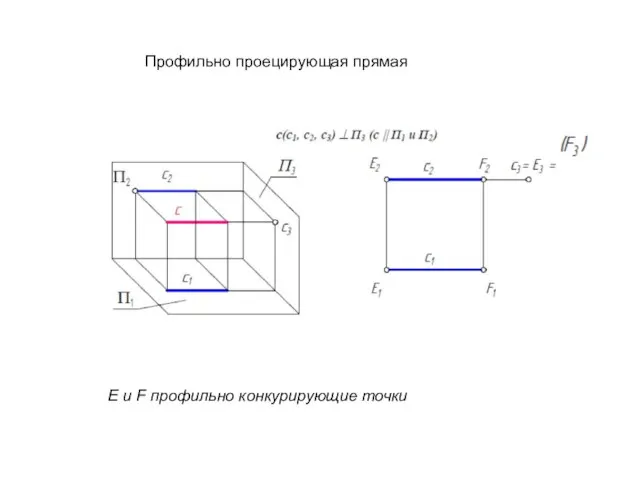
- 29. Профильно проецирующая прямая E и F профильно конкурирующие точки
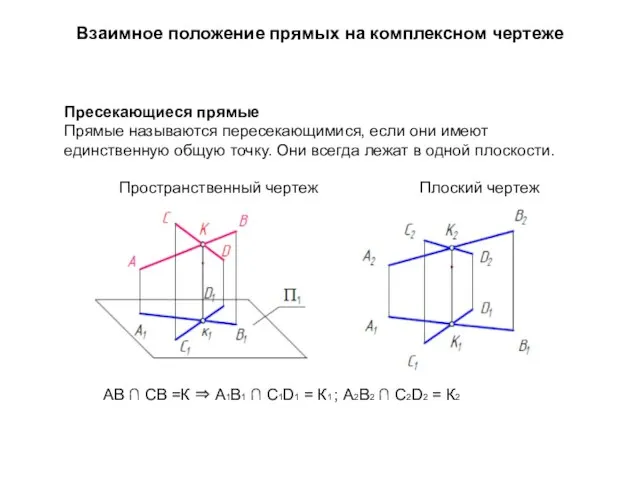
- 30. Взаимное положение прямых на комплексном чертеже Пресекающиеся прямые Прямые называются пересекающимися, если они имеют единственную общую
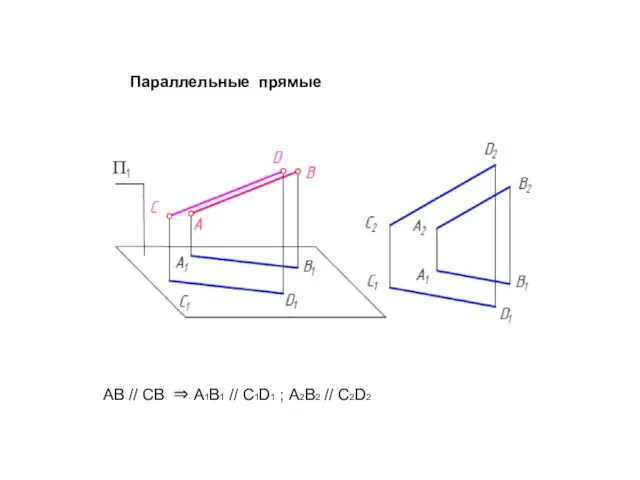
- 31. Параллельные прямые АВ // СВ ⇒ А1В1 // С1D1 ; А2В2 // С2D2
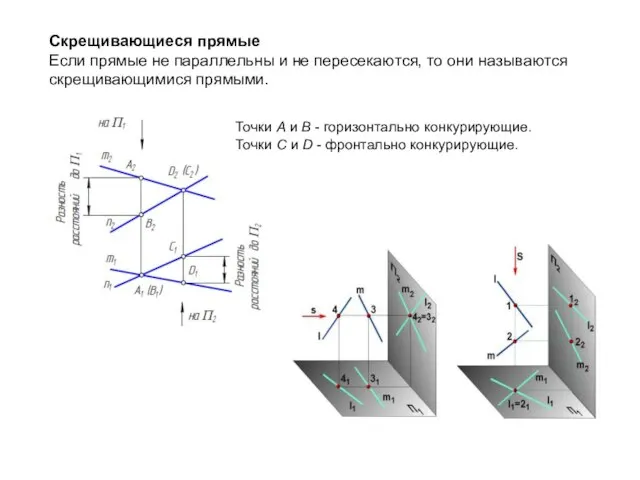
- 32. Скрещивающиеся прямые Если прямые не параллельны и не пересекаются, то они называются скрещивающимися прямыми. Точки А
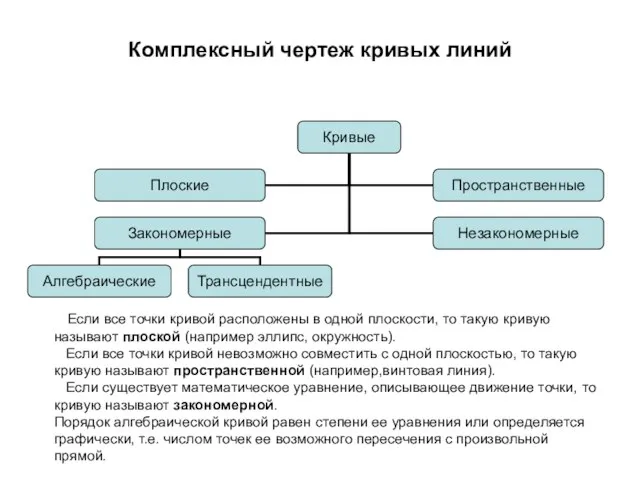
- 33. Комплексный чертеж кривых линий Если все точки кривой расположены в одной плоскости, то такую кривую называют
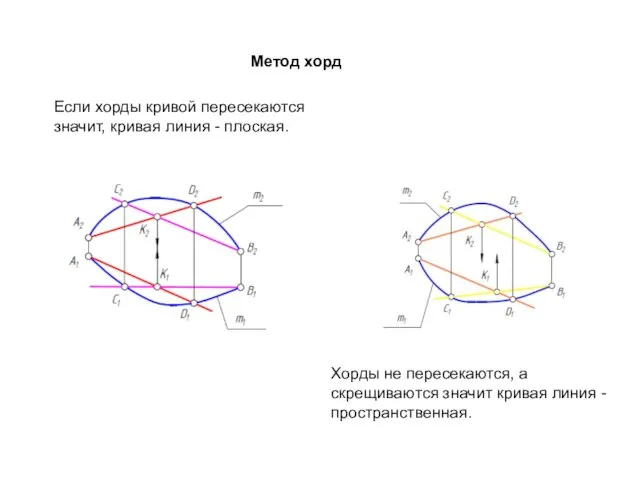
- 34. Метод хорд Если хорды кривой пересекаются значит, кривая линия - плоская. Хорды не пересекаются, а скрещиваются
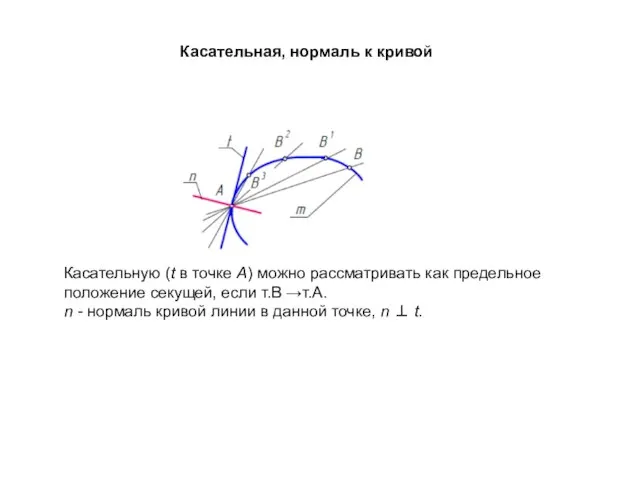
- 35. Касательная, нормаль к кривой Касательную (t в точке А) можно рассматривать как предельное положение секущей, если
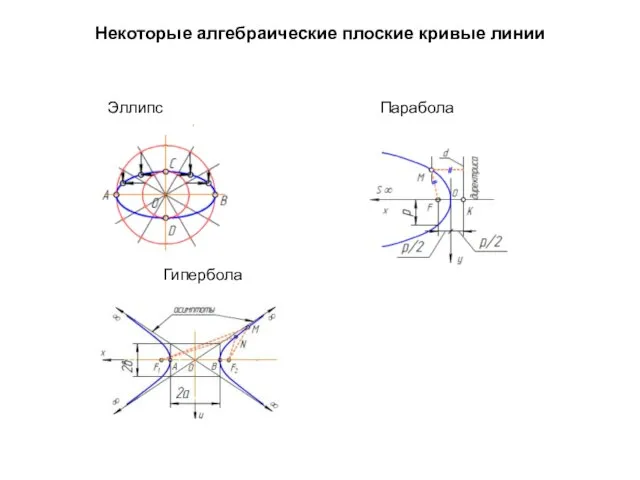
- 36. Некоторые алгебраические плоские кривые линии Эллипс Парабола Гипербола
- 38. Скачать презентацию



 Расчет стержня при растяжении-сжатии
Расчет стержня при растяжении-сжатии Технический рисунок. Урок черчения
Технический рисунок. Урок черчения Разрезы. Правила выполнения разрезов
Разрезы. Правила выполнения разрезов Проекции геометрических тел
Проекции геометрических тел Графическое изображение деталей и изделий. (Индустриальные технологии. 5 класс)
Графическое изображение деталей и изделий. (Индустриальные технологии. 5 класс) Выбор установочных элементов
Выбор установочных элементов Преобразование чертежа заменой плоскостей проекций
Преобразование чертежа заменой плоскостей проекций Чертежи фасадов зданий. Последовательность вычерчивания фасада здания. Наименование фасадов здания на чертеже
Чертежи фасадов зданий. Последовательность вычерчивания фасада здания. Наименование фасадов здания на чертеже Расчетные длины элементов стальных конструкций
Расчетные длины элементов стальных конструкций Сырғанау подшипниктерін дайындау жағдайларында технологиялық процесін әзірлеу
Сырғанау подшипниктерін дайындау жағдайларында технологиялық процесін әзірлеу Виды линий, масштабы
Виды линий, масштабы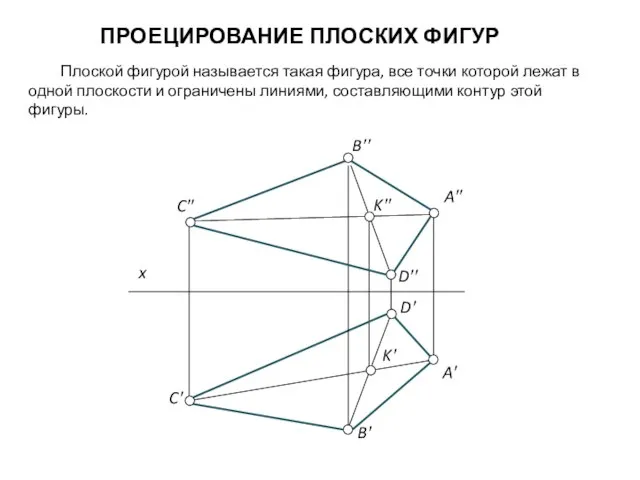 Проецирование плоских фигур
Проецирование плоских фигур Инженерная графика. Виды графики. (Лекция 1)
Инженерная графика. Виды графики. (Лекция 1) Чтение и выполнение чертежей деталей
Чтение и выполнение чертежей деталей Сопряжение (скругление)
Сопряжение (скругление)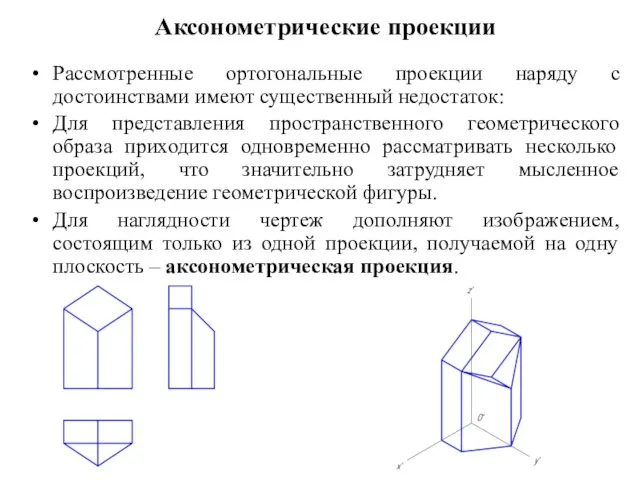 Аксонометрические проекции
Аксонометрические проекции Задание для зачета
Задание для зачета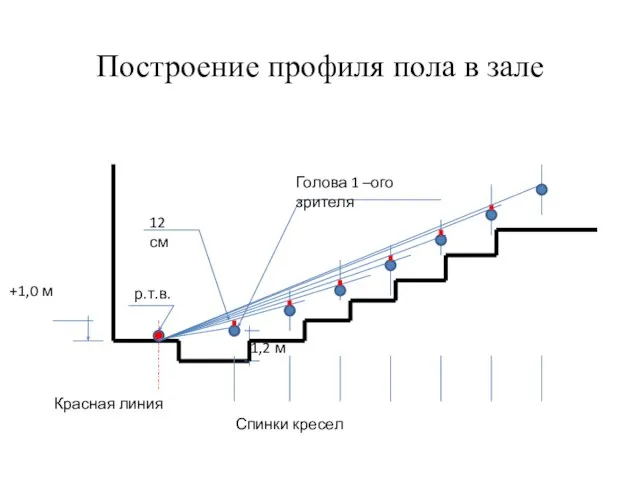 Построение профиля в зале
Построение профиля в зале Резьбовые соединения деталей
Резьбовые соединения деталей Композиция чертежа, проецирование. (Черчение, 10-11 класс)
Композиция чертежа, проецирование. (Черчение, 10-11 класс) Учебно-методический комплекс начертательная геометрия и инженерная графика разработан для студентов специальности Дизайн
Учебно-методический комплекс начертательная геометрия и инженерная графика разработан для студентов специальности Дизайн Проецирование. Технический рисунок. Альбом
Проецирование. Технический рисунок. Альбом Чертёжный стандартный шрифт
Чертёжный стандартный шрифт Сопряжения. Построение сопряжений
Сопряжения. Построение сопряжений Взаимное пересечение поверхностей вращения
Взаимное пересечение поверхностей вращения Изображения – виды, разрезы, сечения
Изображения – виды, разрезы, сечения Задание точки, прямой, плоскости и многогранников на комплексном чертеже
Задание точки, прямой, плоскости и многогранников на комплексном чертеже Начертательная геометрия с использованием мультимедийного компонента
Начертательная геометрия с использованием мультимедийного компонента