Содержание
- 2. Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим
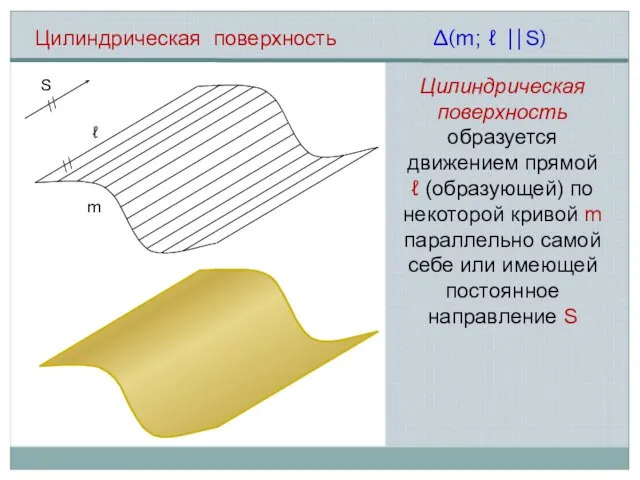
- 3. Цилиндрическая поверхность ℓ m ∆(m; ℓ ⎜⎜S) S // // Цилиндрическая поверхность образуется движением прямой ℓ
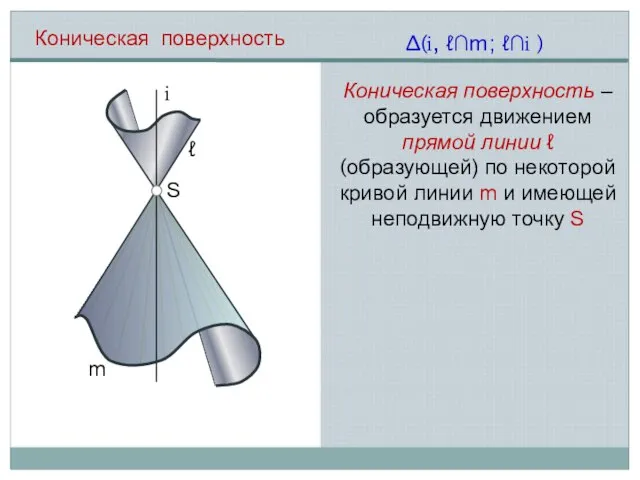
- 4. i m ℓ ∆(i, ℓ∩m; ℓ∩i ) Коническая поверхность Коническая поверхность – образуется движением прямой линии
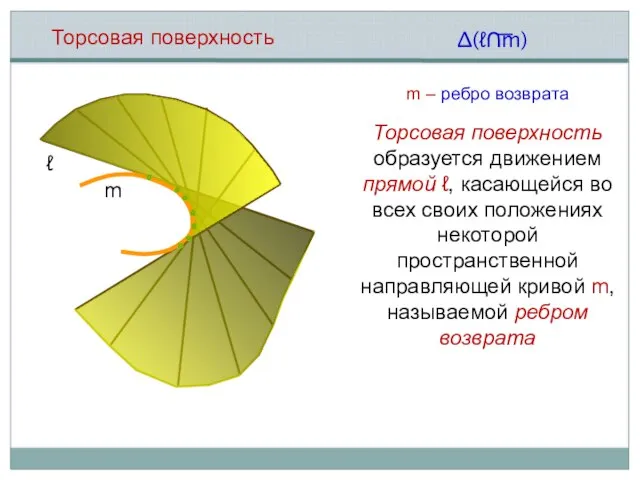
- 5. Торсовая поверхность m m – ребро возврата ℓ ∆(ℓ∩m) Торсовая поверхность образуется движением прямой ℓ, касающейся
- 6. Однополостный гиперболоид
- 7. Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей Многогранником называется тело, ограниченное многогранной поверхностью,
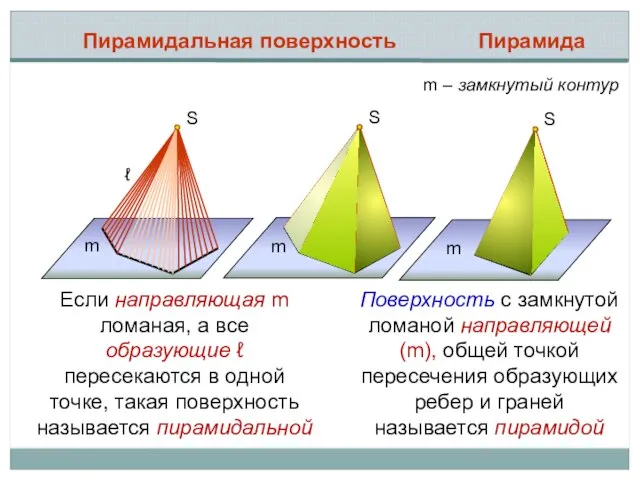
- 8. S ℓ m S m Пирамидальная поверхность S m Пирамида m – замкнутый контур Если направляющая
- 9. Принадлежность точки поверхности
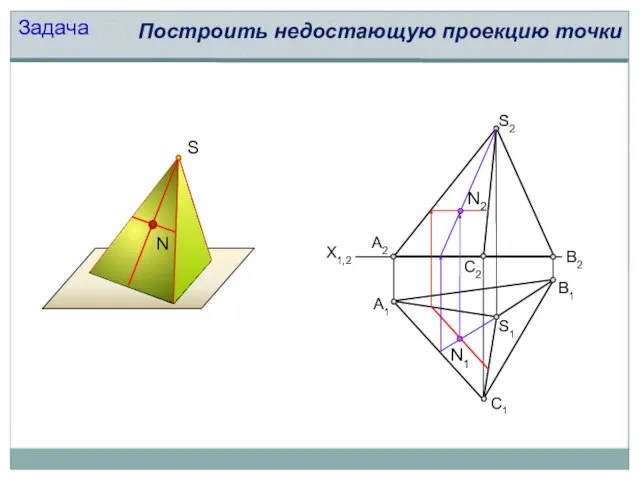
- 10. S А1 С1 В1 S2 X1,2 S1 А2 С2 В2 Задача Построить недостающую проекцию точки N
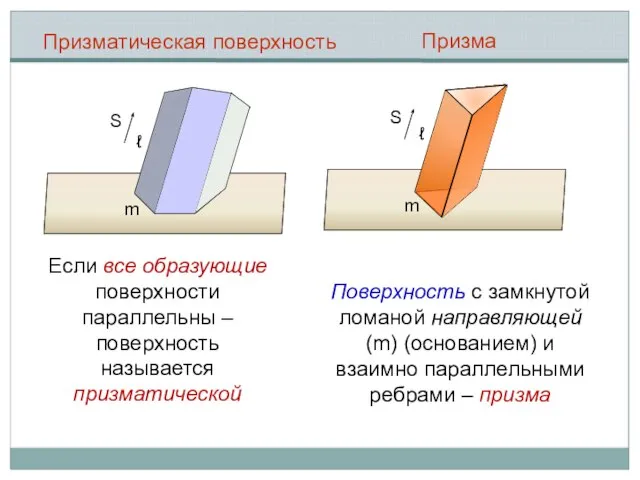
- 11. m S ℓ Призматическая поверхность m S ℓ Призма Если все образующие поверхности параллельны – поверхность
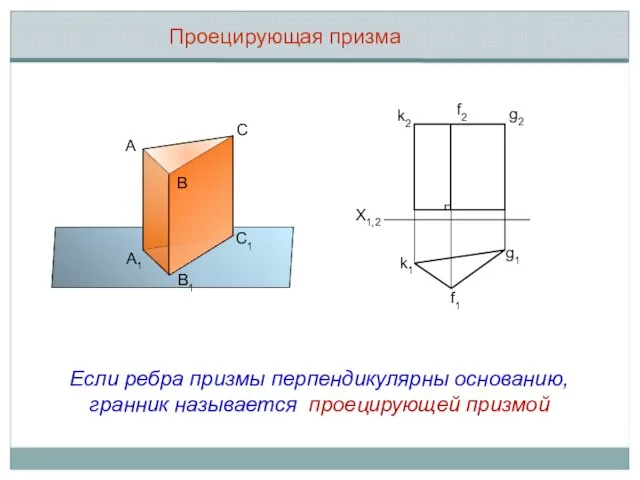
- 12. Проецирующая призма А В С С1 В1 А1 k2 k1 f1 g1 g2 f2 X1,2 Если
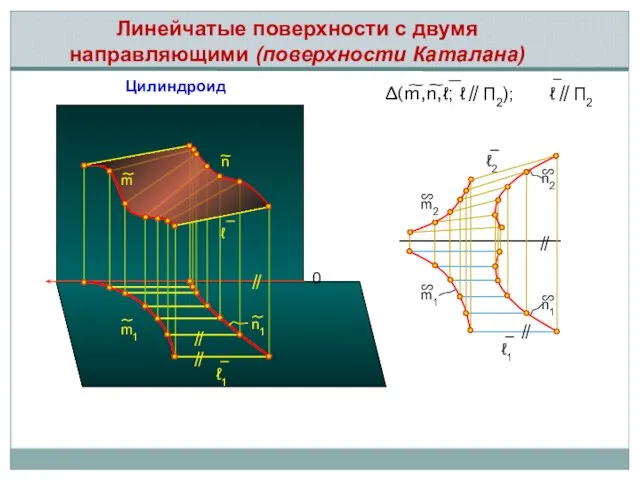
- 13. Поверхности Каталана
- 14. 0 m1 n1 ℓ ℓ1 ℓ1 n m n1 ∽ m1 ∽ ℓ2 m2 ∽ n2
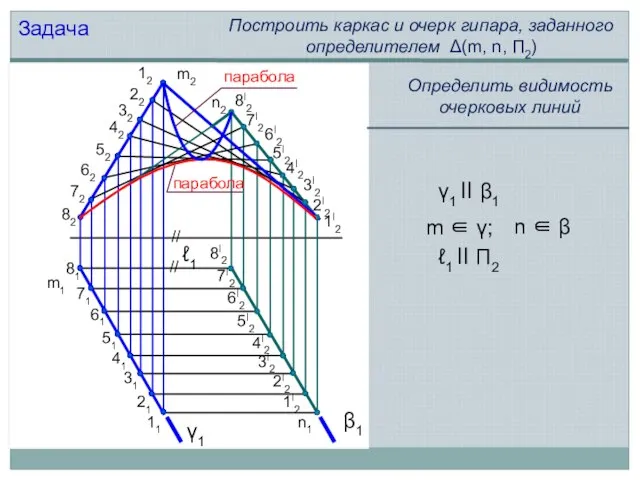
- 15. Поверхность с плоскостью параллелизма и двумя скрещивающимися направляющими называется гиперболическим параболоидом, или косой плоскостью Гипар
- 16. m2 n2 n1 m1 Задача Построить каркас и очерк гипара, заданного определителем Δ(m, n, П2) 12
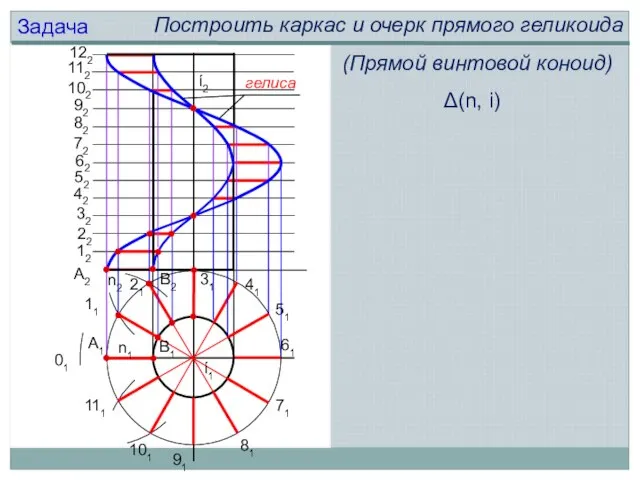
- 17. Винтовой поверхностью называют поверхность, образованную винтовым движением образующей Винтовым движением называют движение, при котором каждая точка
- 18. n2 n1 гелиса А1 В1 ί1 ί2 Задача Построить каркас и очерк прямого геликоида А2 В2
- 20. Скачать презентацию






 Строительные чертежи
Строительные чертежи Изображение - виды, разрезы, сечения
Изображение - виды, разрезы, сечения Правила разработки схем. Черчение схем
Правила разработки схем. Черчение схем Размеры ступеней и подступеней. Лекция 9
Размеры ступеней и подступеней. Лекция 9 Шрифт чертежный
Шрифт чертежный Изображения – виды. Изображения на чертежах
Изображения – виды. Изображения на чертежах Инженерная графика
Инженерная графика Общие требования и правила оформления текстовой, графической и конструкторской документации
Общие требования и правила оформления текстовой, графической и конструкторской документации Инженерная графика. Практика
Инженерная графика. Практика Типовые соединения деталей. Обозначение метрической резьбы
Типовые соединения деталей. Обозначение метрической резьбы Основные правила нанесения размеров. Лекция № 2
Основные правила нанесения размеров. Лекция № 2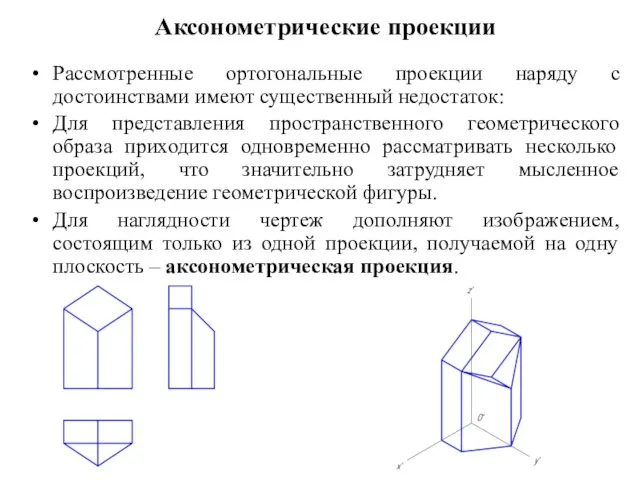 Аксонометрические проекции
Аксонометрические проекции Сопряжения. Инженерная графика
Сопряжения. Инженерная графика Линия. Лекция 6
Линия. Лекция 6 Соединения деталей машин
Соединения деталей машин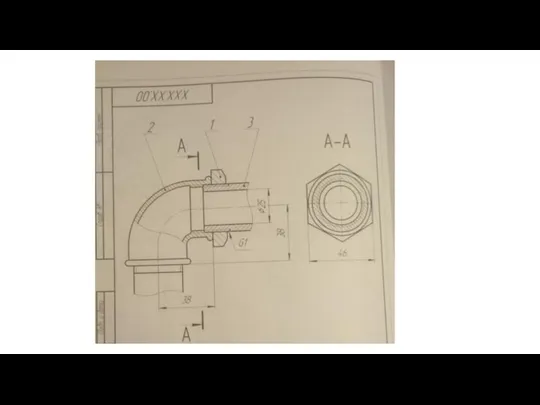 Угольники и тройники
Угольники и тройники Расчет и оптимизация кронштейна
Расчет и оптимизация кронштейна Отклонения и допуски расположения рассматриваемого элемента (ГОСТ 24642-83)
Отклонения и допуски расположения рассматриваемого элемента (ГОСТ 24642-83) Геометрические построения на чертежах
Геометрические построения на чертежах Технический рисунок. Урок черчения
Технический рисунок. Урок черчения Пересечение линии и поверхности
Пересечение линии и поверхности Изображения – виды, разрезы, сечения ГОСТ 2.305-68
Изображения – виды, разрезы, сечения ГОСТ 2.305-68 Конструкторско-технологическое обеспечение проекта туристического агентства Мир на ладони
Конструкторско-технологическое обеспечение проекта туристического агентства Мир на ладони Черчение это единый международный технический, графический язык
Черчение это единый международный технический, графический язык Строительное черчение. Назначение строительных чертежей. Урок № 6
Строительное черчение. Назначение строительных чертежей. Урок № 6 Реконструкция ремонтной мастерской в ЗАО ПЗ Ленинский путь с разработкой настольного пневматического пресса
Реконструкция ремонтной мастерской в ЗАО ПЗ Ленинский путь с разработкой настольного пневматического пресса Проект планировки участка линейного объекта улично-дорожной сети – районы Алексеевский и Ростокино
Проект планировки участка линейного объекта улично-дорожной сети – районы Алексеевский и Ростокино Эскиз и последовательность его выполнения
Эскиз и последовательность его выполнения