Содержание
- 2. ПРОЕЦИРОВАНИЕ ТОЧКИ
- 3. ВВЕДЕНИЕ Чертеж – это своеобразный язык, с помощью которого, используя всего лишь точки, линии и ограниченное
- 4. Леон Батиста Альберти (1404-1472) – итальянский ученый. Теоретическая разработка основ перспективы; способ построения перспективы с помощью
- 5. Альберт Дюрер (1471-1528) – немецкий художник и гравер. Разработал основы рисования; графические способы построения плоских и
- 6. Возникновение начертательной геометрии как науки связывают с именем французского математика и инженера Гаспара Монжа (1746—1818). Выдающиеся
- 7. Первым русским ученым, связавшим свою судьбу с начертательной геометрией, был Яков Александрович Севастьянов (1796—1849) — профессор
- 8. Предмет начертательной геометрии. Начертательная геометрия – раздел геометрии. Предметом НГ является изложение и обоснование способов изображения
- 9. Образование проекций. Методы проецирования. В курсе НГ под проецированием понимается отображение пространственного образа на плоскость, которую
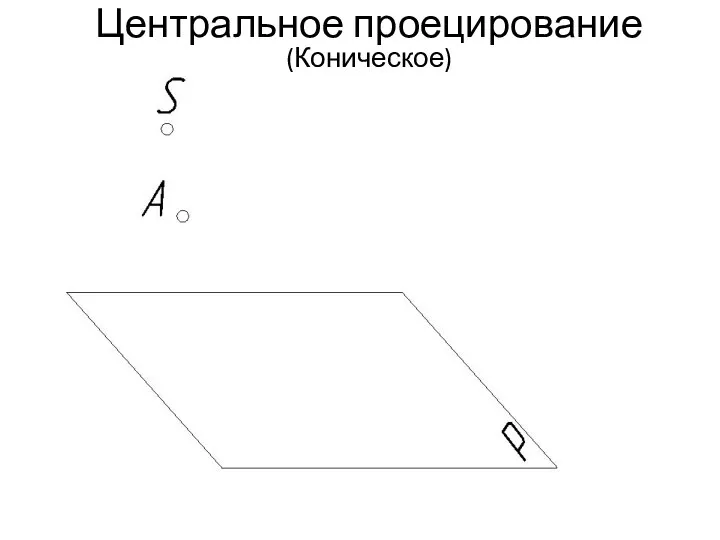
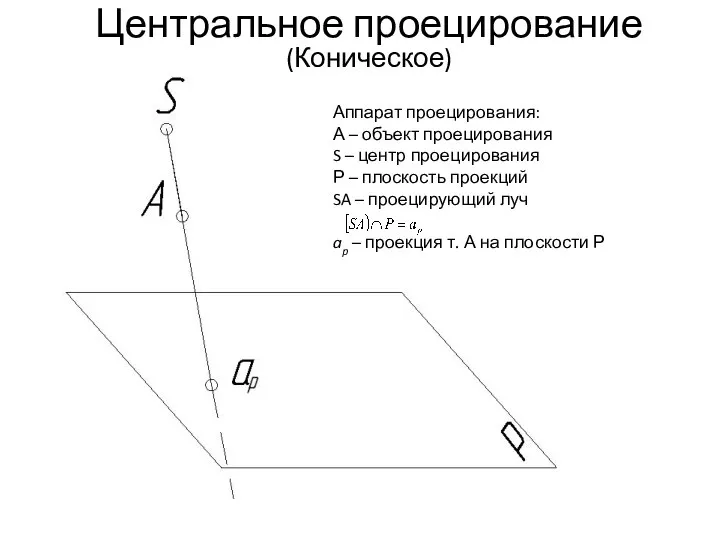
- 10. Центральное проецирование (Коническое)
- 11. ( Аппарат проецирования: А – объект проецирования S – центр проецирования Р – плоскость проекций SA
- 12. Свойства проецирования: Проекцией точки называют точку пересечения проецирующего луча с ПП. Каждая точка пространства имеет единственную
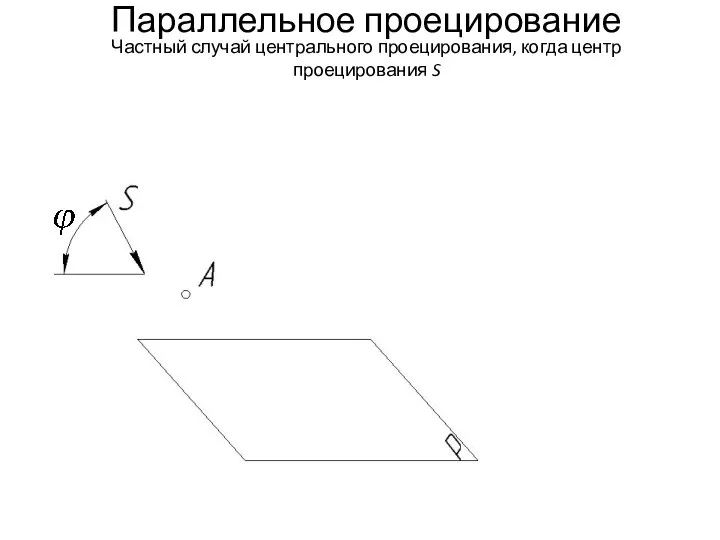
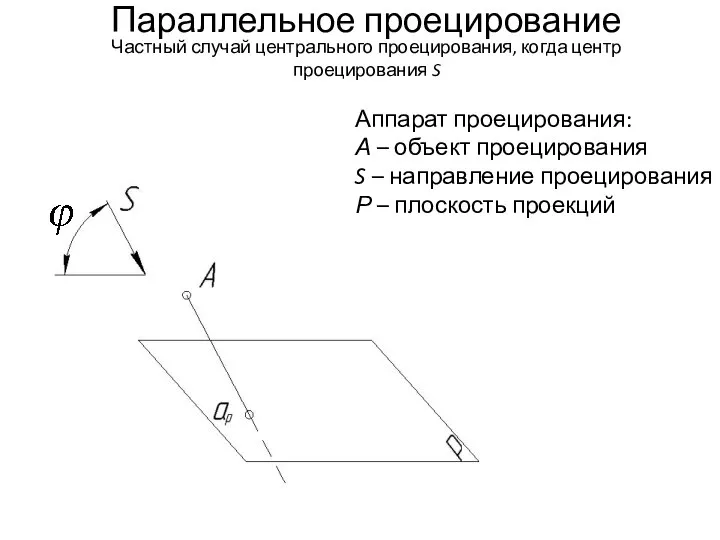
- 13. Параллельное проецирование Частный случай центрального проецирования, когда центр проецирования S
- 14. Аппарат проецирования: А – объект проецирования S – направление проецирования Р – плоскость проекций Параллельное проецирование
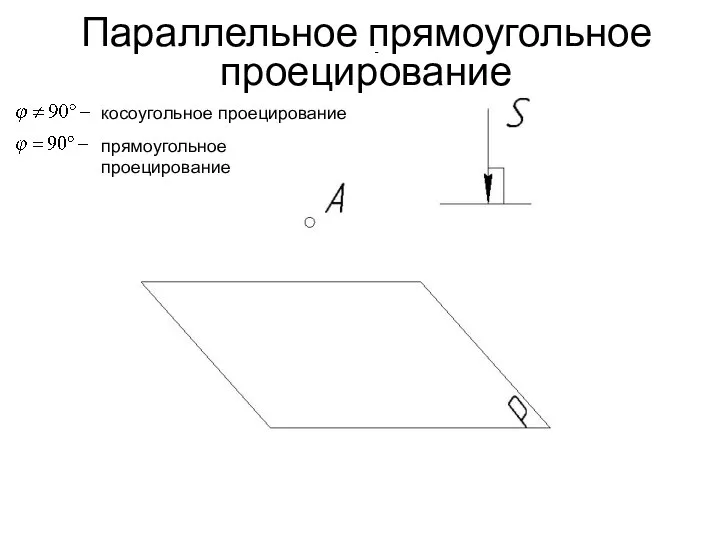
- 15. Параллельное прямоугольное проецирование - косоугольное проецирование прямоугольное проецирование
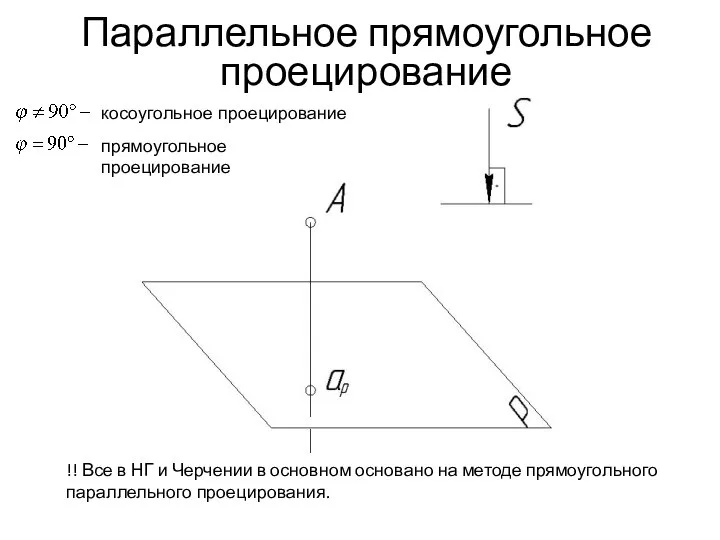
- 16. Параллельное прямоугольное проецирование косоугольное проецирование прямоугольное проецирование !! Все в НГ и Черчении в основном основано
- 17. Для получения ортогонального чертежа обладающего свойством “обратимости” необходимо иметь, по крайней мере, две связанные между собой
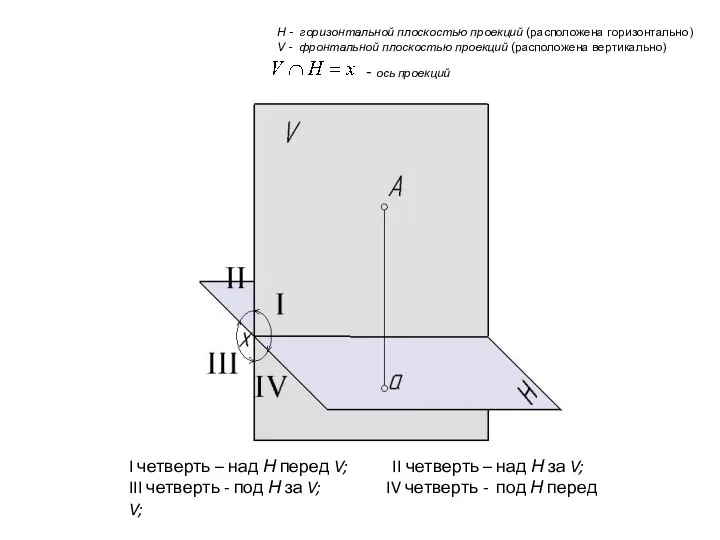
- 19. Н - горизонтальной плоскостью проекций (расположена горизонтально) V - фронтальной плоскостью проекций (расположена вертикально) - ось
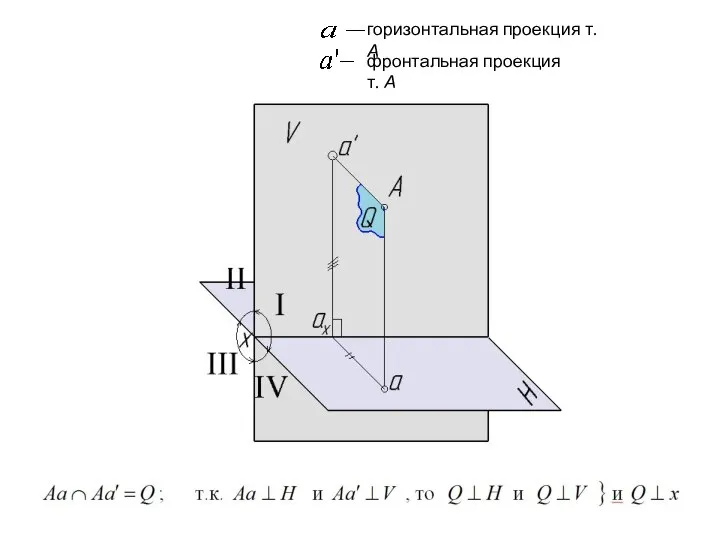
- 20. горизонтальная проекция т. А фронтальная проекция т. А
- 21. Теорема: проекции некоторой точки получаются расположенными на прямых перпендикулярных к оси проекций и пересекающих эту ось
- 24. Проецирование точки на три взаимно-перпендикулярные ПП В практике составления чертежа изделия зачастую необходимо не две, а
- 25. Три взаимно перпендикулярные плоскости попарно пересекаются по трем прямым - осям проекций x, y и z,
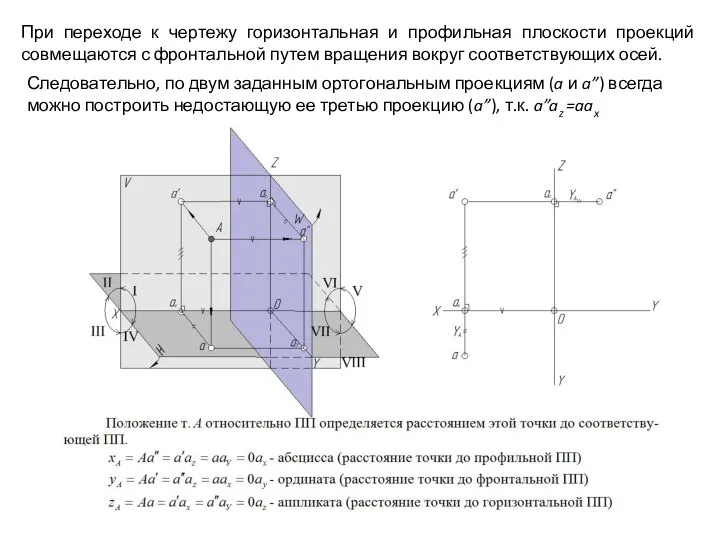
- 28. При переходе к чертежу горизонтальная и профильная плоскости проекций совмещаются с фронтальной путем вращения вокруг соответствующих
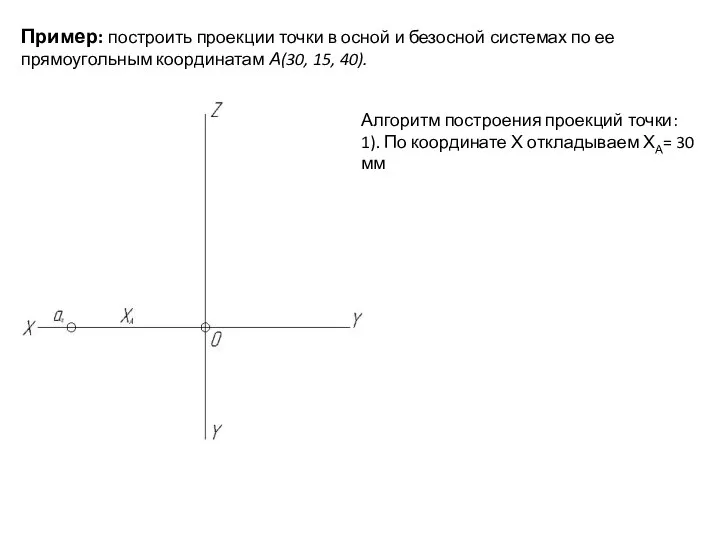
- 29. Пример: построить проекции точки в осной и безосной системах по ее прямоугольным координатам А(30, 15, 40).
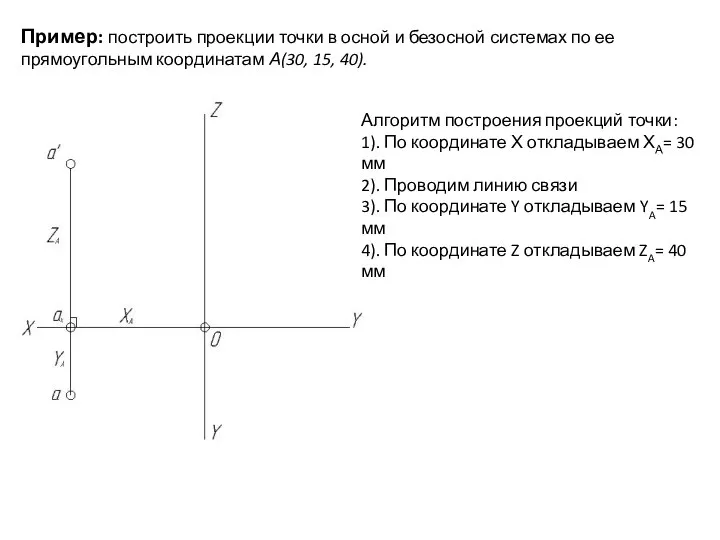
- 30. Пример: построить проекции точки в осной и безосной системах по ее прямоугольным координатам А(30, 15, 40).
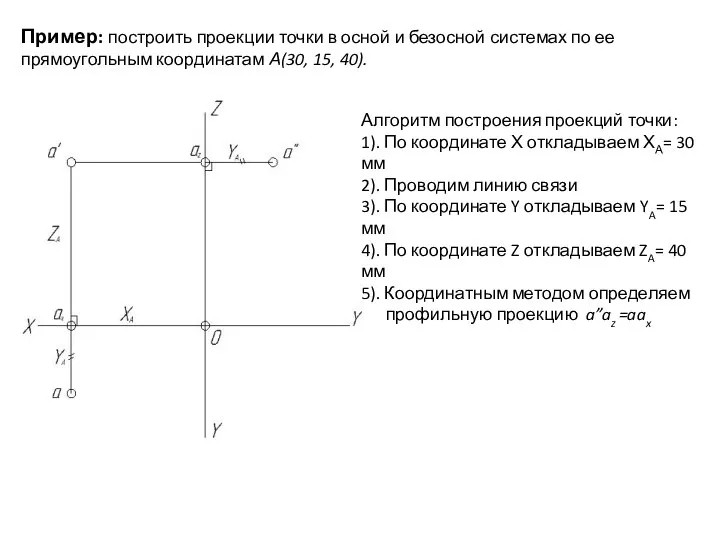
- 31. Пример: построить проекции точки в осной и безосной системах по ее прямоугольным координатам А(30, 15, 40).
- 32. Пример: построить проекции точки в осной и безосной системах по ее прямоугольным координатам А(30, 15, 40).
- 33. Пример: построить проекции точки в осной и безосной системах по ее прямоугольным координатам А(30, 15, 40).
- 34. ПРЕЦИРОВАНИЕ ПРЯМОЙ
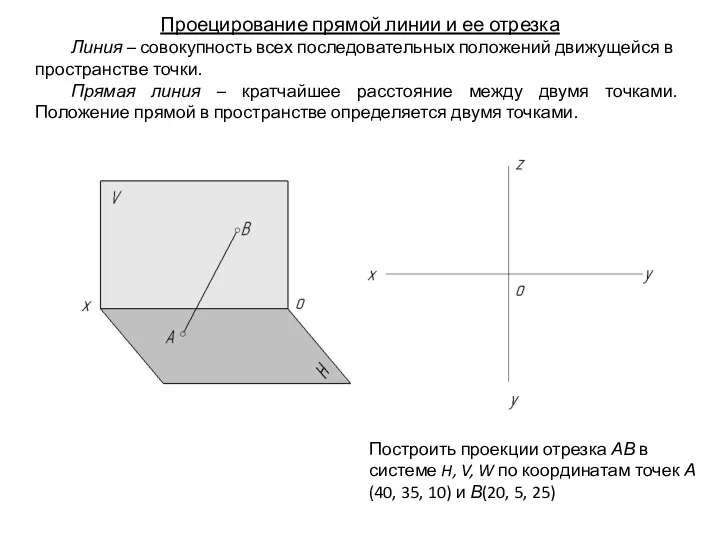
- 35. Проецирование прямой линии и ее отрезка Линия – совокупность всех последовательных положений движущейся в пространстве точки.
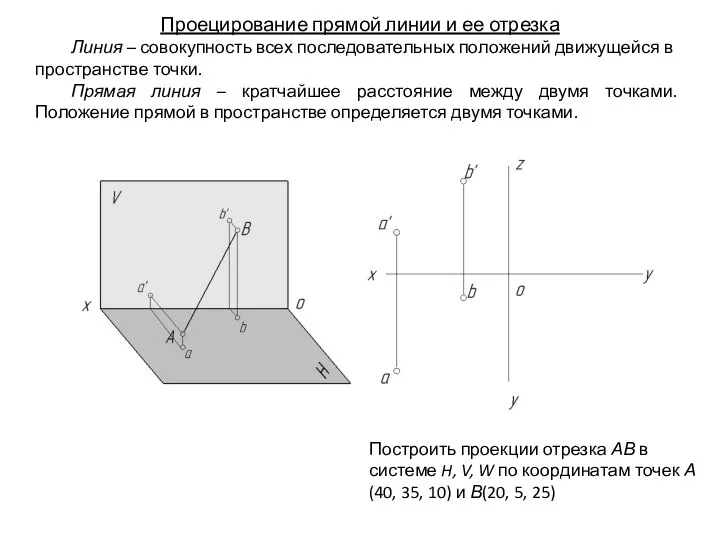
- 36. Проецирование прямой линии и ее отрезка Линия – совокупность всех последовательных положений движущейся в пространстве точки.
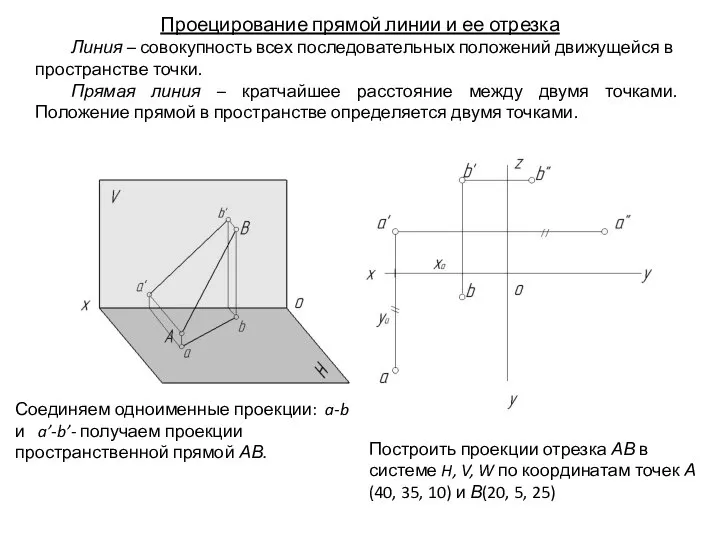
- 37. Проецирование прямой линии и ее отрезка Линия – совокупность всех последовательных положений движущейся в пространстве точки.
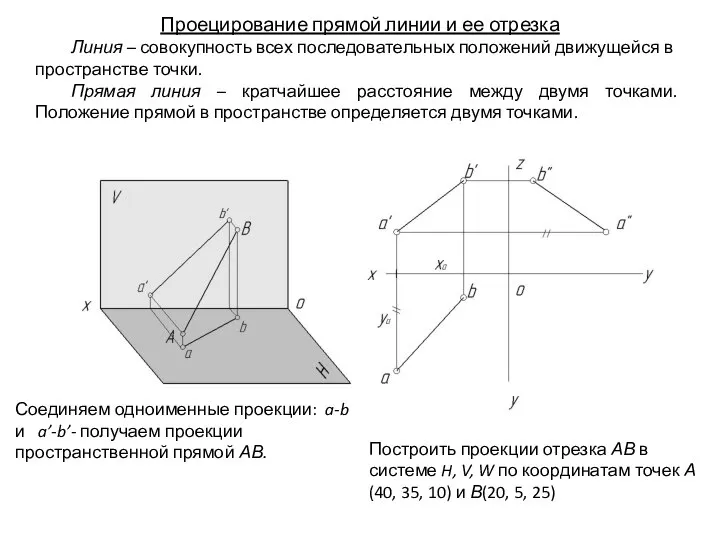
- 38. Проецирование прямой линии и ее отрезка Линия – совокупность всех последовательных положений движущейся в пространстве точки.
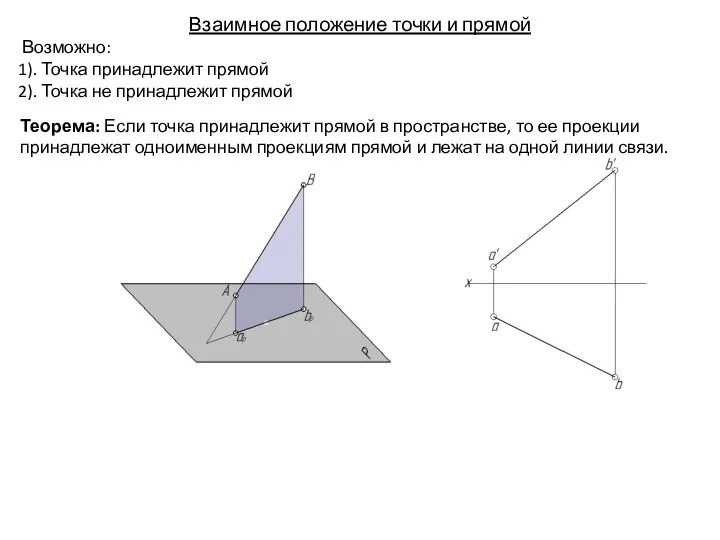
- 39. Взаимное положение точки и прямой Возможно: 1). Точка принадлежит прямой 2). Точка не принадлежит прямой Теорема:
- 40. Взаимное положение точки и прямой Возможно: 1). Точка принадлежит прямой 2). Точка не принадлежит прямой Теорема:
- 41. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
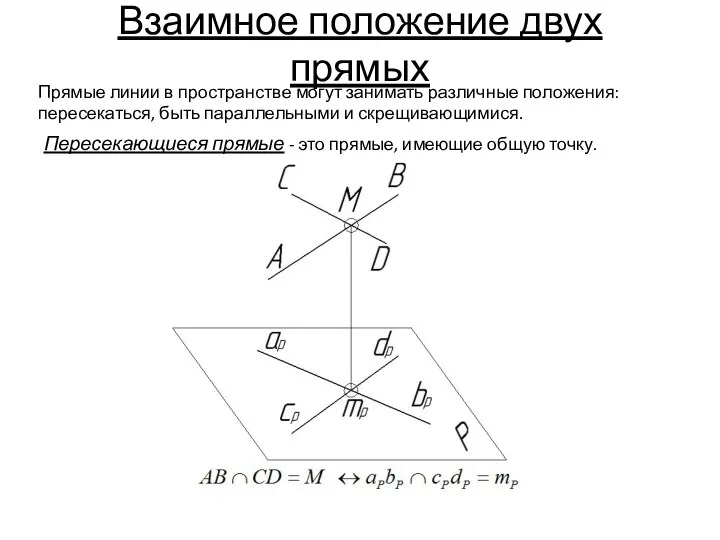
- 42. Взаимное положение двух прямых Прямые линии в пространстве могут занимать различные положения: пересекаться, быть параллельными и
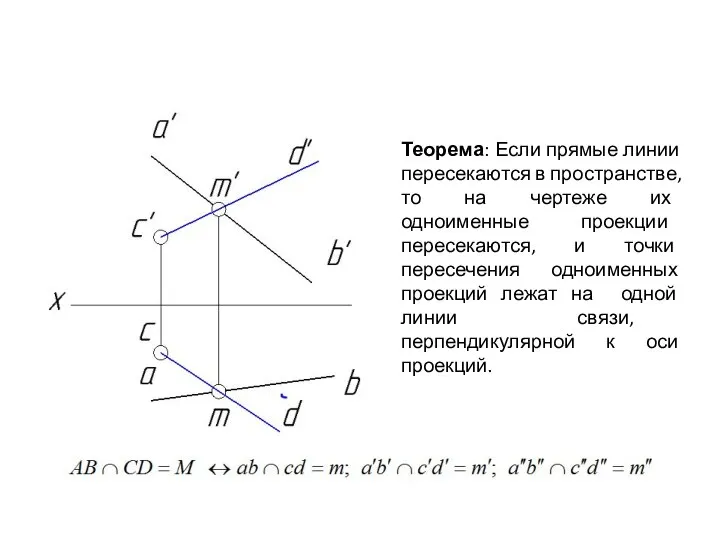
- 44. Теорема: Если прямые линии пересекаются в пространстве, то на чертеже их одноименные проекции пересекаются, и точки
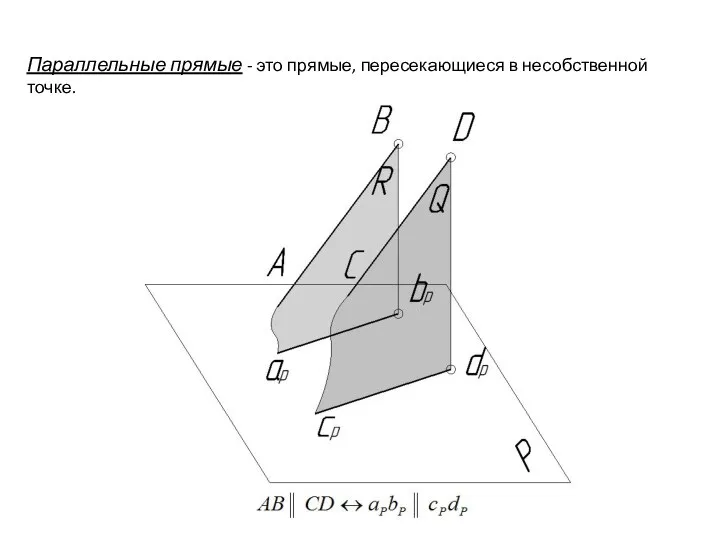
- 45. Параллельные прямые - это прямые, пересекающиеся в несобственной точке.
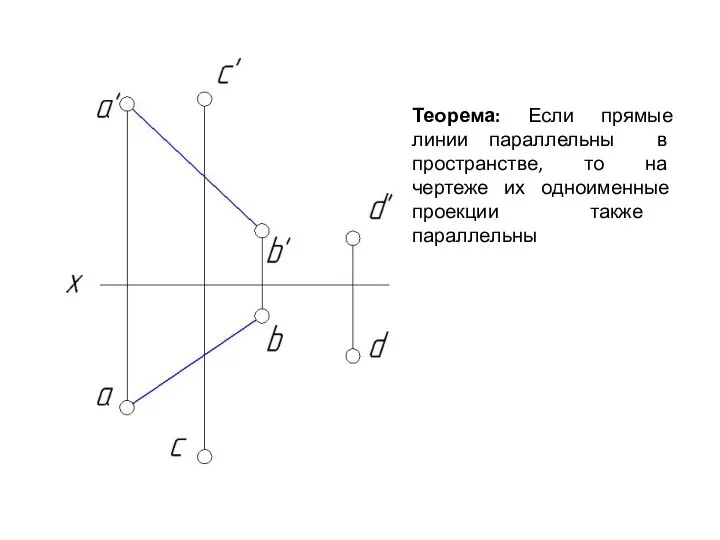
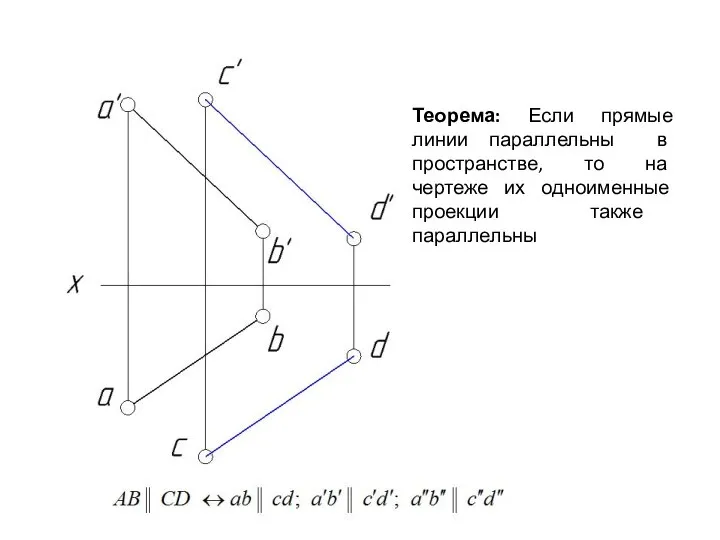
- 46. Теорема: Если прямые линии параллельны в пространстве, то на чертеже их одноименные проекции также параллельны
- 47. Теорема: Если прямые линии параллельны в пространстве, то на чертеже их одноименные проекции также параллельны
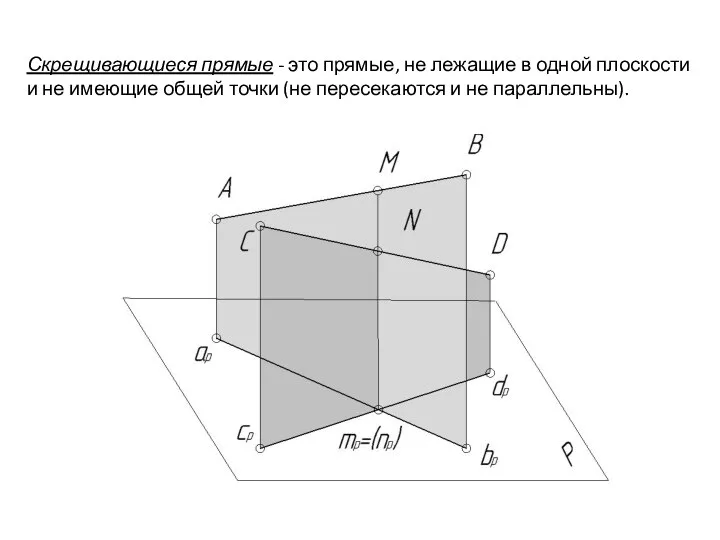
- 48. Скрещивающиеся прямые - это прямые, не лежащие в одной плоскости и не имеющие общей точки (не
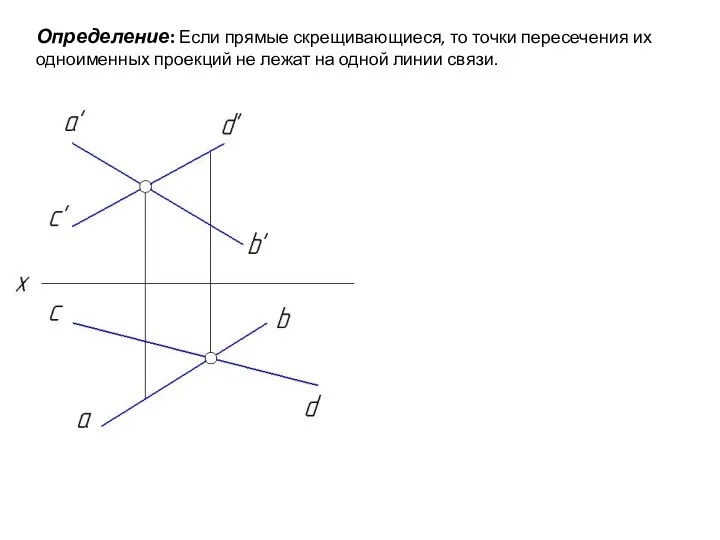
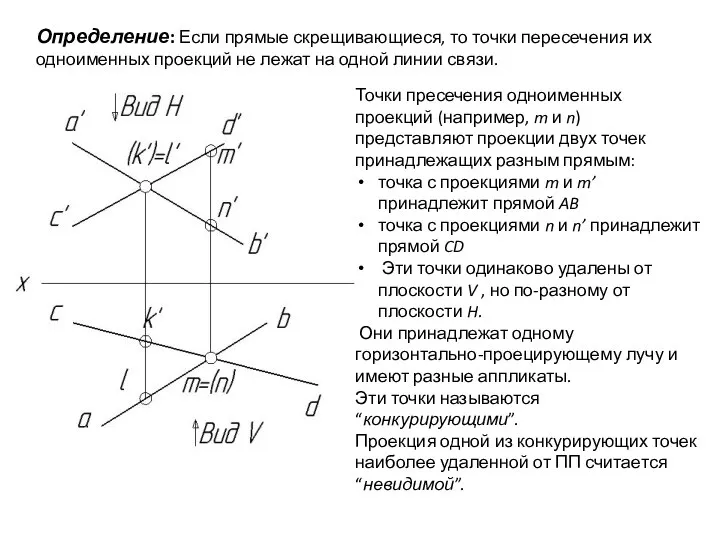
- 49. Определение: Если прямые скрещивающиеся, то точки пересечения их одноименных проекций не лежат на одной линии связи.
- 50. Определение: Если прямые скрещивающиеся, то точки пересечения их одноименных проекций не лежат на одной линии связи.
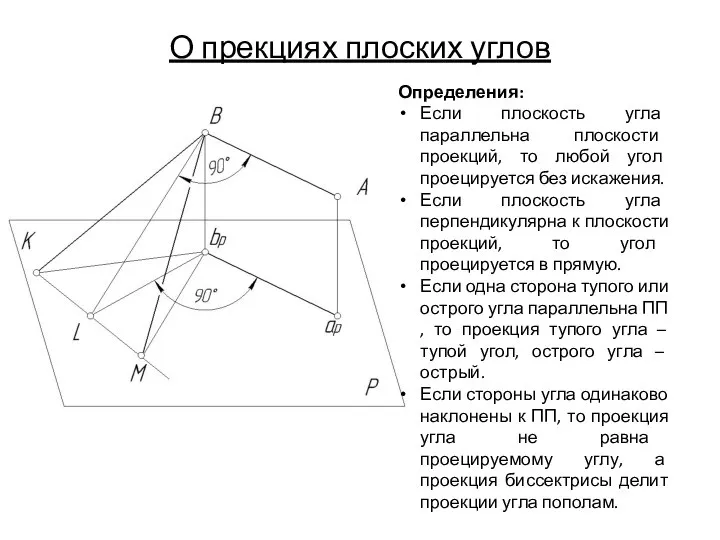
- 51. О прекциях плоских углов Определения: Если плоскость угла параллельна плоскости проекций, то любой угол проецируется без
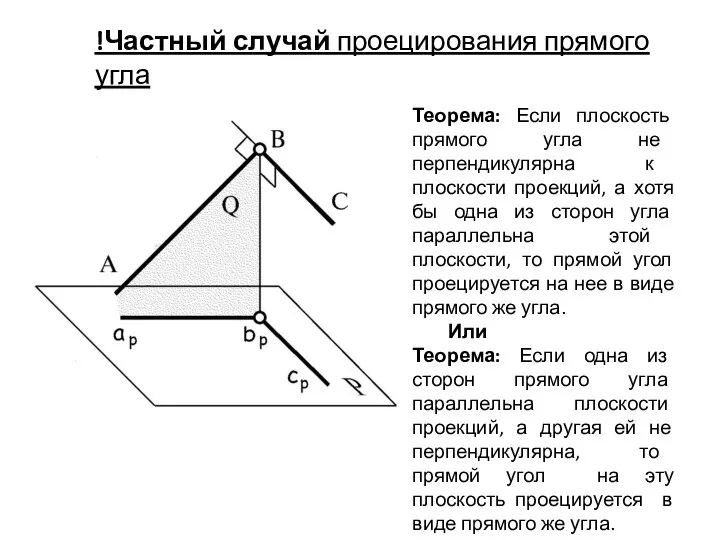
- 52. Теорема: Если плоскость прямого угла не перпендикулярна к плоскости проекций, а хотя бы одна из сторон
- 53. !Частный случай проецирования прямого угла
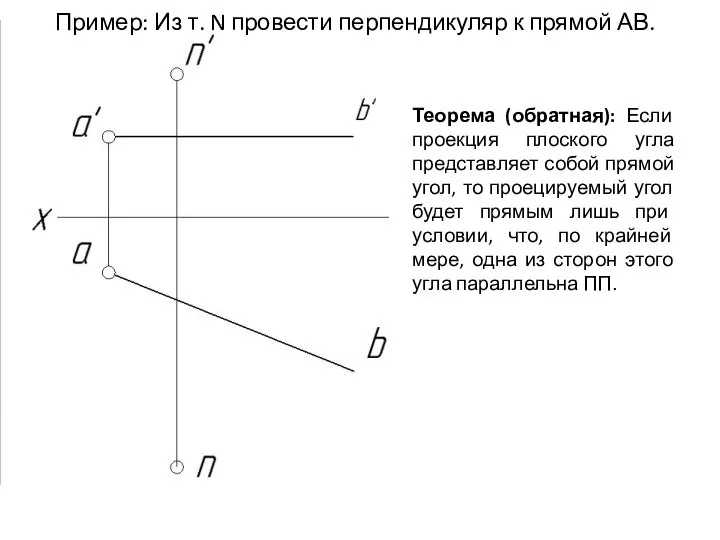
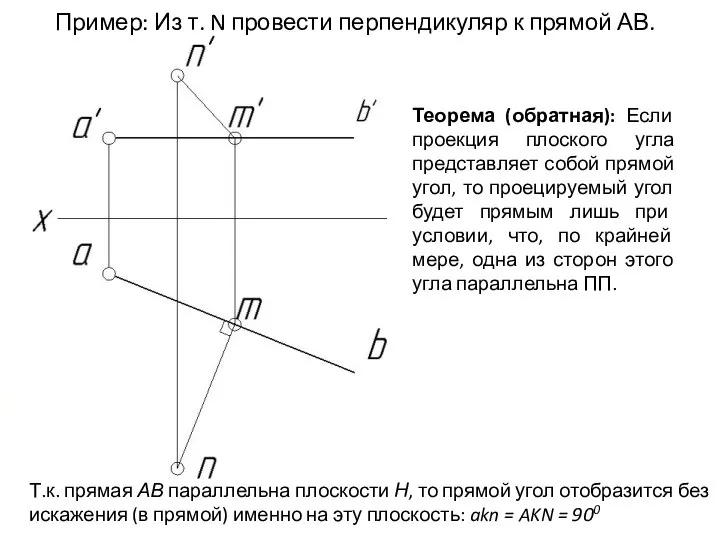
- 54. Теорема (обратная): Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь
- 55. Теорема (обратная): Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь
- 56. Теорема (обратная): Если проекция плоского угла представляет собой прямой угол, то проецируемый угол будет прямым лишь
- 57. ПЛОСКОСТЬ
- 58. ПЛОСКОСТЬ Поверхность – совокупность всех последовательных положений движущейся в пространстве линии. В ВМ плоскость является простейшей
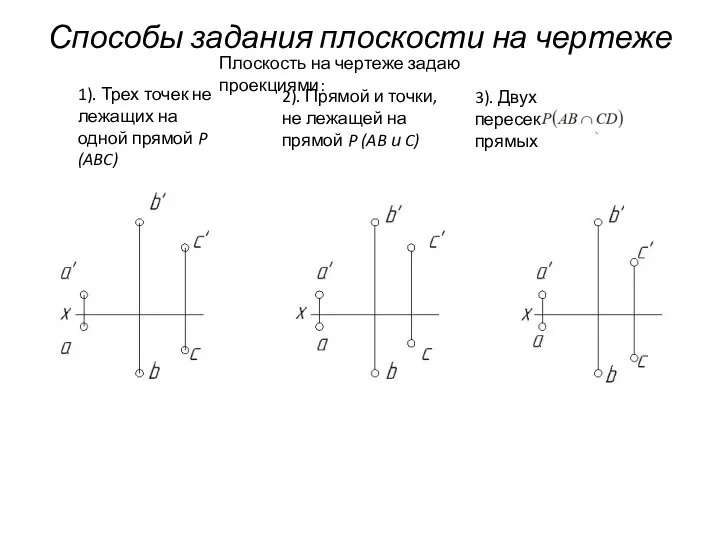
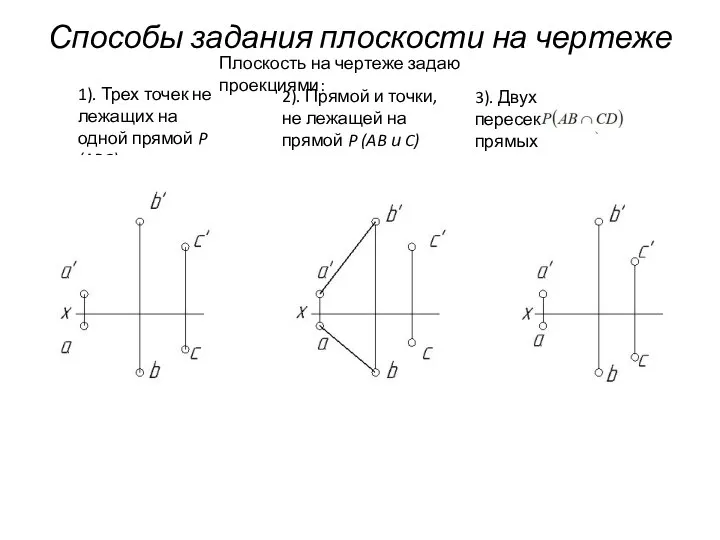
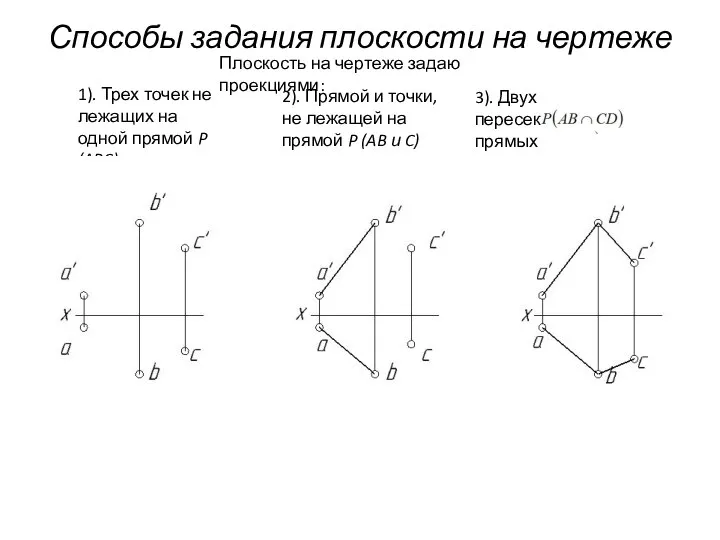
- 59. Способы задания плоскости на чертеже Плоскость на чертеже задаю проекциями: 1). Трех точек не лежащих на
- 60. Способы задания плоскости на чертеже Плоскость на чертеже задаю проекциями: 1). Трех точек не лежащих на
- 61. Способы задания плоскости на чертеже Плоскость на чертеже задаю проекциями: 1). Трех точек не лежащих на
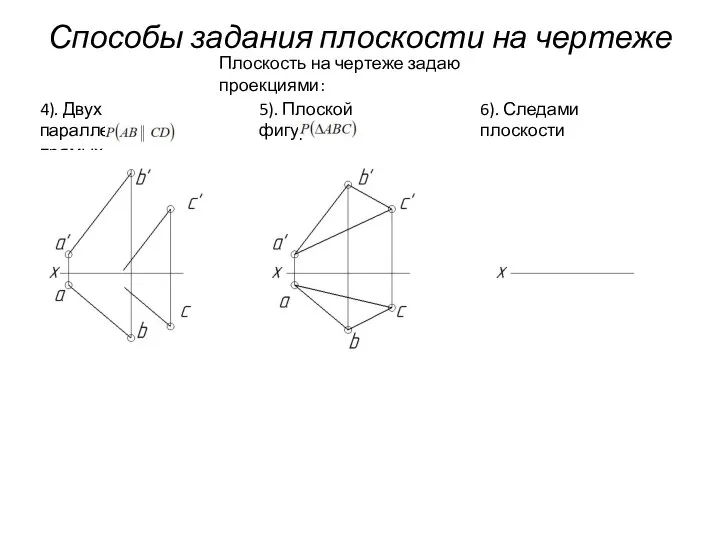
- 62. Способы задания плоскости на чертеже Плоскость на чертеже задаю проекциями: 4). Двух параллельных прямых 5). Плоской
- 63. Способы задания плоскости на чертеже Плоскость на чертеже задаю проекциями: 4). Двух параллельных прямых 5). Плоской
- 64. Способы задания плоскости на чертеже Плоскость на чертеже задаю проекциями: 4). Двух параллельных прямых 5). Плоской
- 65. Способы задания плоскости на чертеже Плоскость на чертеже задаю проекциями: 4). Двух параллельных прямых 5). Плоской
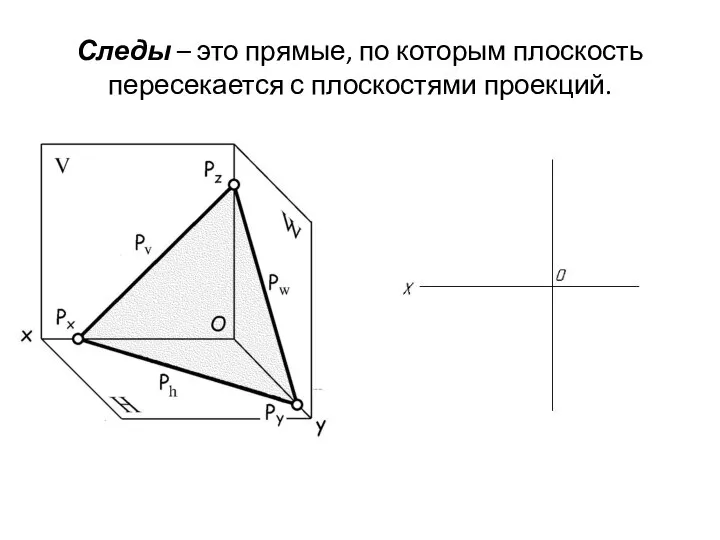
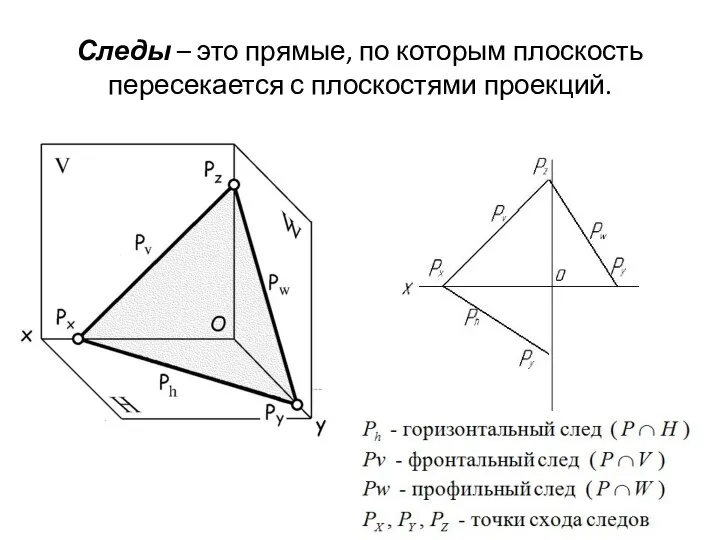
- 66. Следы – это прямые, по которым плоскость пересекается с плоскостями проекций.
- 67. Следы – это прямые, по которым плоскость пересекается с плоскостями проекций.
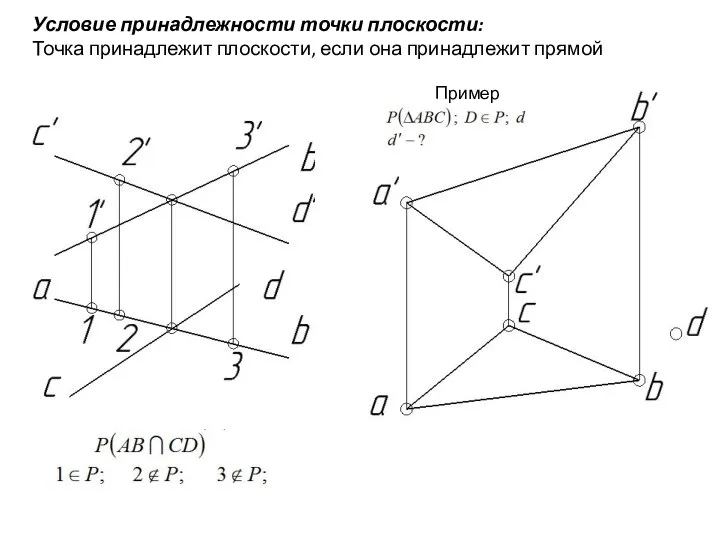
- 68. Условие принадлежности точки плоскости: Точка принадлежит плоскости, если она принадлежит прямой Пример:
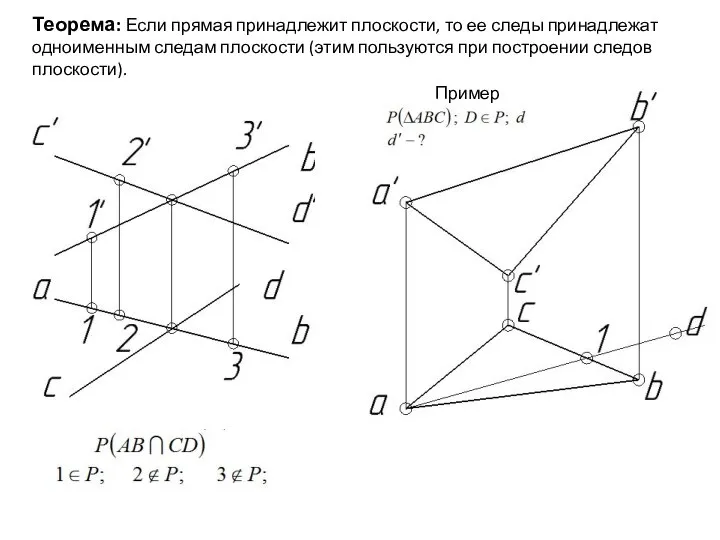
- 69. Теорема: Если прямая принадлежит плоскости, то ее следы принадлежат одноименным следам плоскости (этим пользуются при построении
- 70. Теорема: Если прямая принадлежит плоскости, то ее следы принадлежат одноименным следам плоскости (этим пользуются при построении
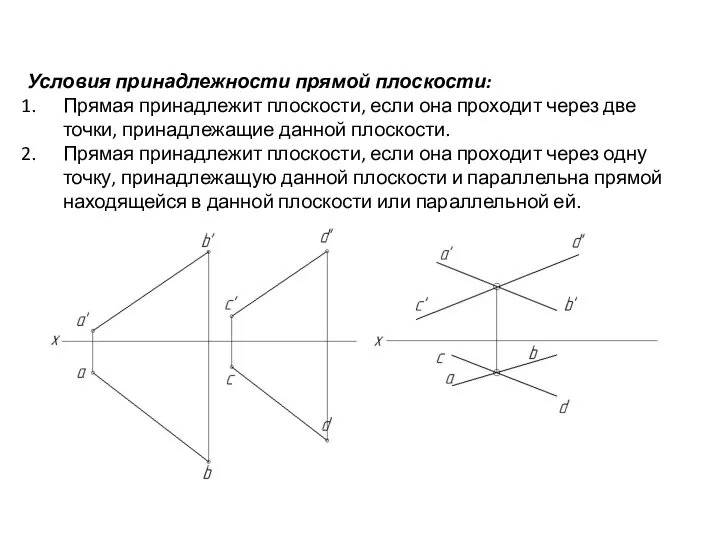
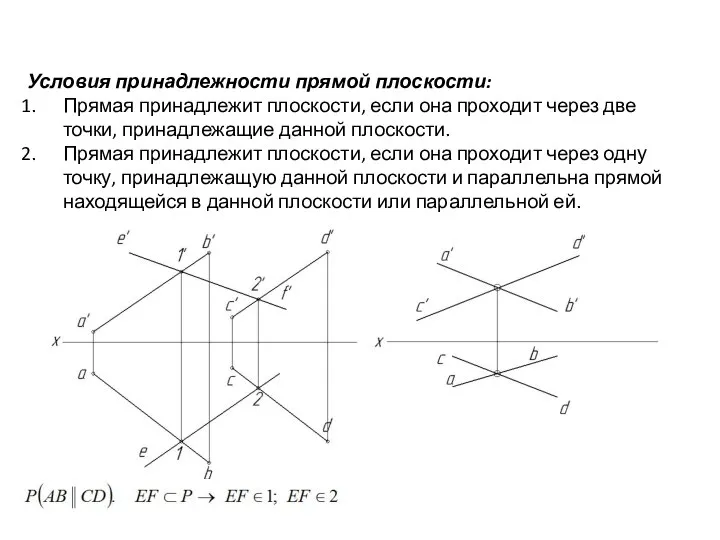
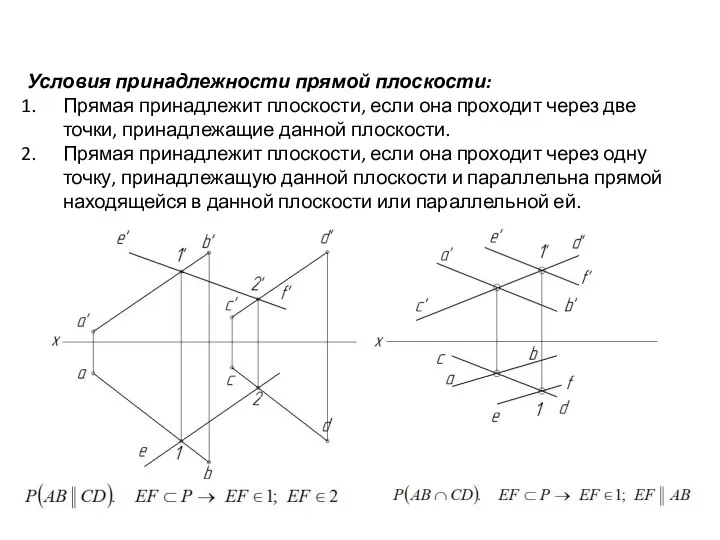
- 71. Условия принадлежности прямой плоскости: Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.
- 72. Условия принадлежности прямой плоскости: Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.
- 73. Условия принадлежности прямой плоскости: Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.
- 74. Положение плоскости относительно плоскостей проекций Возможны: 1). Плоскость не перпендикулярна ни одной ПП 2). Плоскость перпендикулярна
- 75. Плоскости перпендикулярна одной или двум ПП – плоскость частного положения Плоскости перпендикулярна одной плоскости проекций –
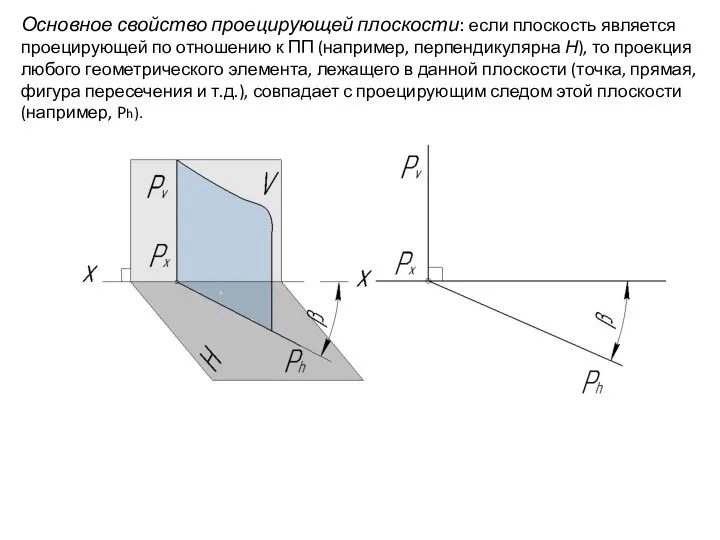
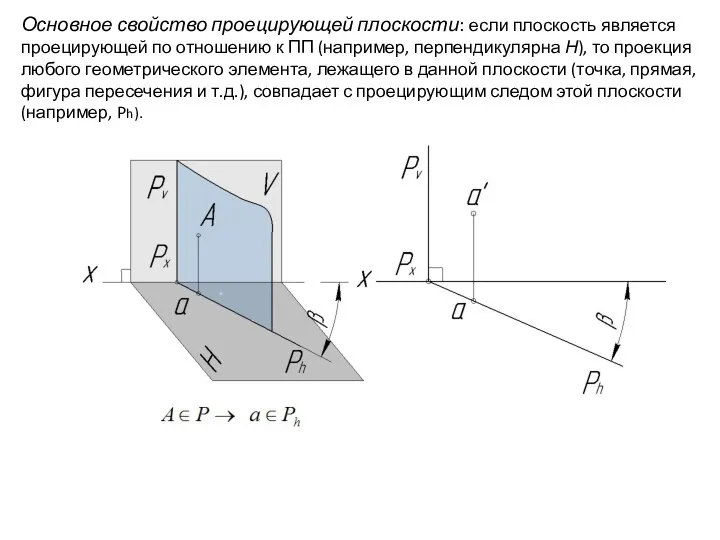
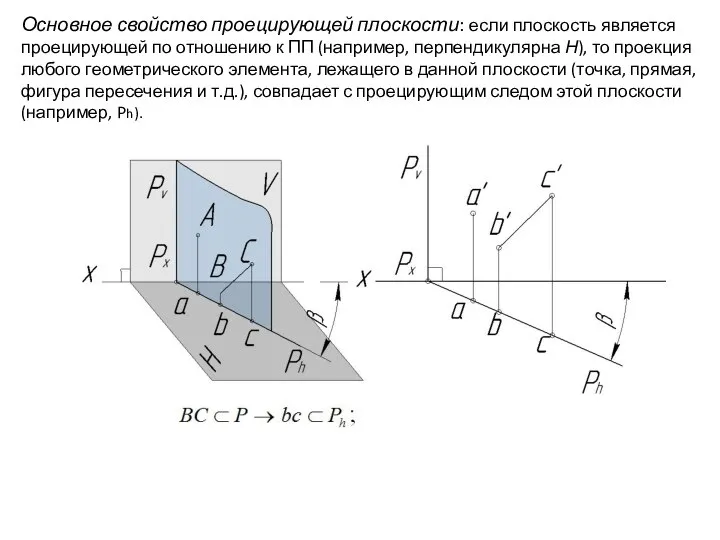
- 76. Основное свойство проецирующей плоскости: если плоскость является проецирующей по отношению к ПП (например, перпендикулярна Н), то
- 77. Основное свойство проецирующей плоскости: если плоскость является проецирующей по отношению к ПП (например, перпендикулярна Н), то
- 78. Основное свойство проецирующей плоскости: если плоскость является проецирующей по отношению к ПП (например, перпендикулярна Н), то
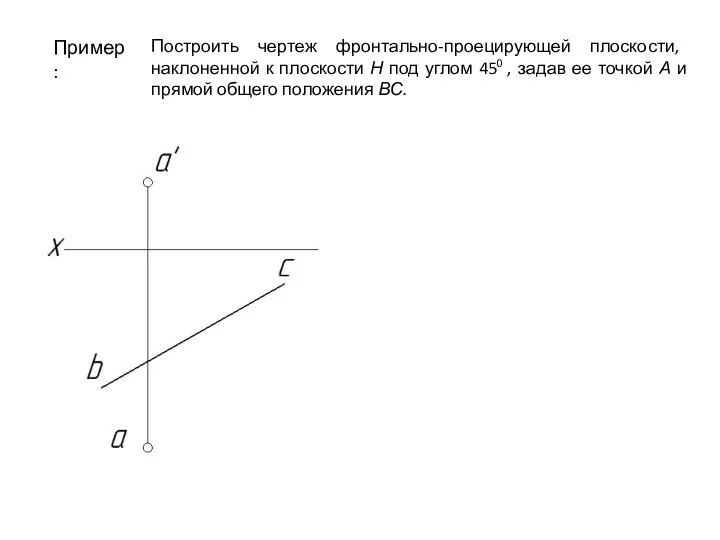
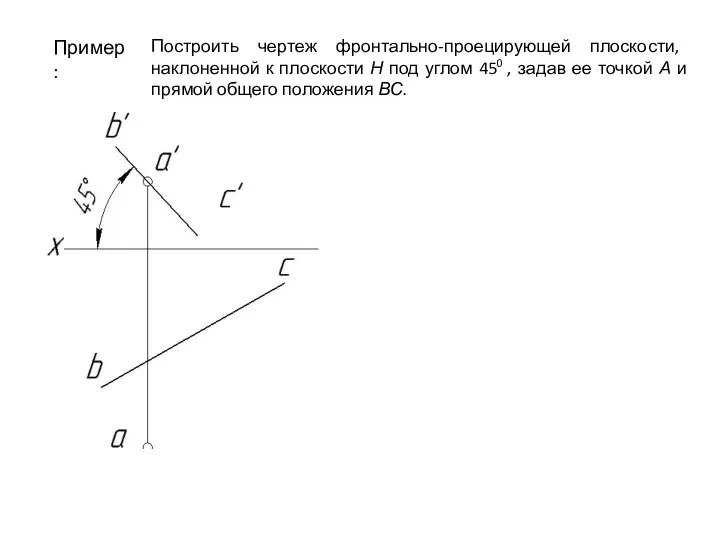
- 79. Пример: Построить чертеж фронтально-проецирующей плоскости, наклоненной к плоскости Н под углом 450 , задав ее точкой
- 80. Пример: Построить чертеж фронтально-проецирующей плоскости, наклоненной к плоскости Н под углом 450 , задав ее точкой
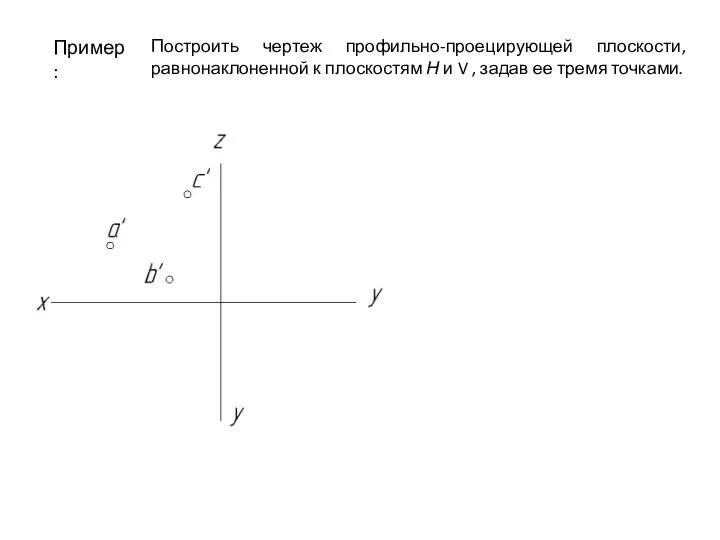
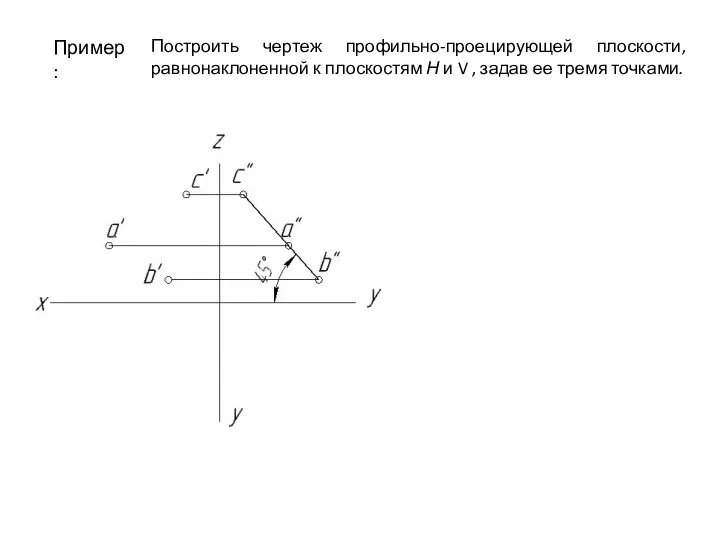
- 81. Пример: Построить чертеж профильно-проецирующей плоскости, равнонаклоненной к плоскостям Н и V , задав ее тремя точками.
- 82. Пример: Построить чертеж профильно-проецирующей плоскости, равнонаклоненной к плоскостям Н и V , задав ее тремя точками.
- 83. Пример: Построить чертеж профильно-проецирующей плоскости, равнонаклоненной к плоскостям Н и V , задав ее тремя точками.
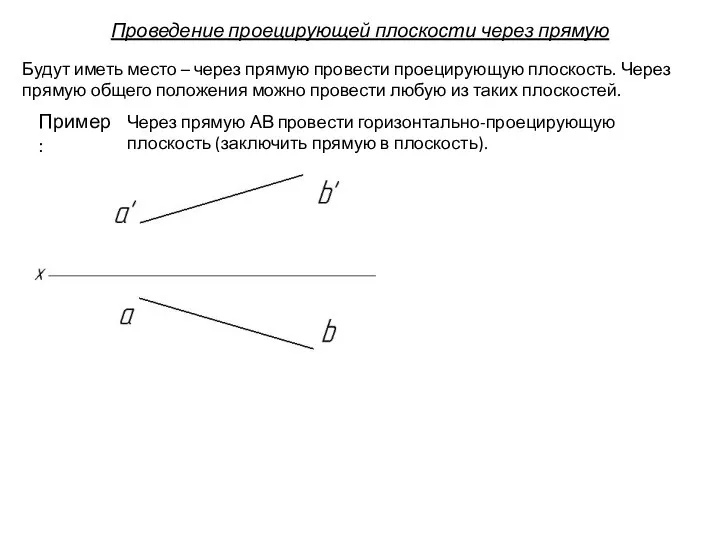
- 84. Проведение проецирующей плоскости через прямую Будут иметь место – через прямую провести проецирующую плоскость. Через прямую
- 85. Проведение проецирующей плоскости через прямую Будут иметь место – через прямую провести проецирующую плоскость. Через прямую
- 86. Проведение проецирующей плоскости через прямую Будут иметь место – через прямую провести проецирующую плоскость. Через прямую
- 87. Проведение проецирующей плоскости через прямую Будут иметь место – через прямую провести проецирующую плоскость. Через прямую
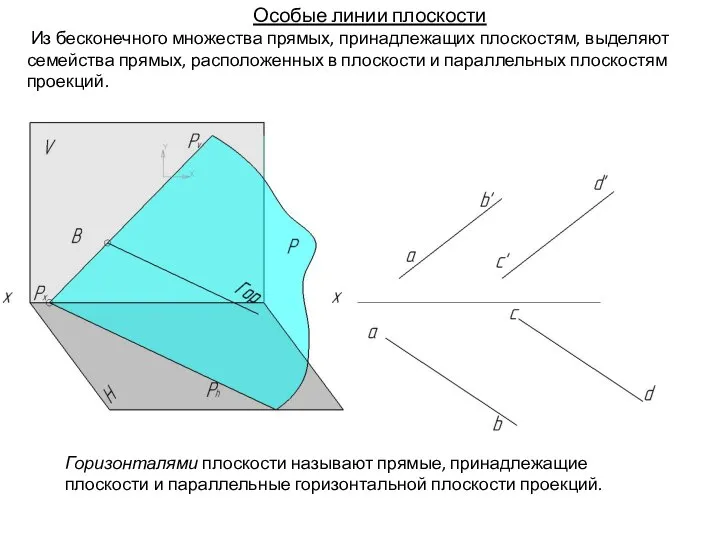
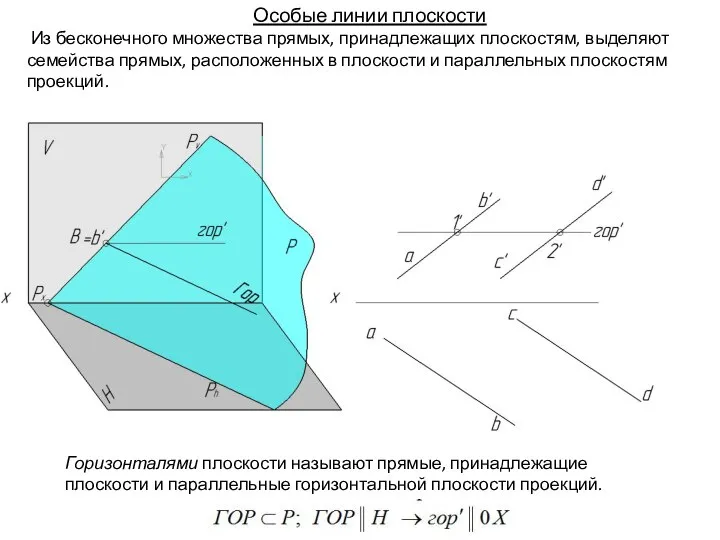
- 88. Особые линии плоскости Из бесконечного множества прямых, принадлежащих плоскостям, выделяют семейства прямых, расположенных в плоскости и
- 89. Особые линии плоскости Из бесконечного множества прямых, принадлежащих плоскостям, выделяют семейства прямых, расположенных в плоскости и
- 91. Скачать презентацию






































 Задачи по инженерной графике
Задачи по инженерной графике Расчёт короба под динамики Dynamic State PSW-40D2 PRO Series
Расчёт короба под динамики Dynamic State PSW-40D2 PRO Series Машиностроительное черчение
Машиностроительное черчение Актуальность предмета
Актуальность предмета Проектирования предприятия отрасли
Проектирования предприятия отрасли Проекции с числовыми отметками
Проекции с числовыми отметками Определение точки пересечения прямой с плоскостью и определение ее видимости
Определение точки пересечения прямой с плоскостью и определение ее видимости Построение комплексного чертежа детали
Построение комплексного чертежа детали Введение. Инженерная и компьютерная графика и её задачи. Методы проецирования. Способы центрального проецирования
Введение. Инженерная и компьютерная графика и её задачи. Методы проецирования. Способы центрального проецирования Модель поверхности
Модель поверхности Нанесение допусков формы и расположения поверхностей
Нанесение допусков формы и расположения поверхностей Виды и их расположение на чертеже
Виды и их расположение на чертеже Геометрические построения на чертежах
Геометрические построения на чертежах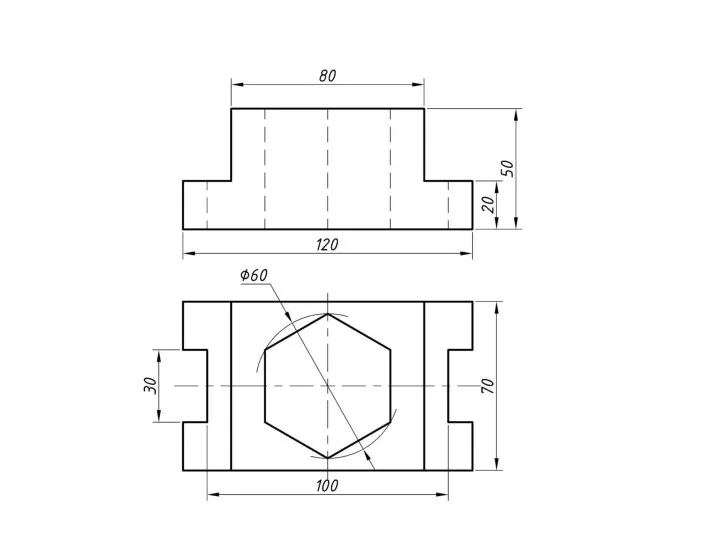 Компоновка чертежа
Компоновка чертежа Проецирование
Проецирование Построение теней в перспективе. Классификация источников освещения
Построение теней в перспективе. Классификация источников освещения Нанесение размеров на чертежах. Применение и обозначение масштабов
Нанесение размеров на чертежах. Применение и обозначение масштабов Начертательная геометрия
Начертательная геометрия Исследование макета криогенного насоса
Исследование макета криогенного насоса Проецирование. Проекция
Проецирование. Проекция Деталирование
Деталирование Геометрические основы теории теней
Геометрические основы теории теней Перспектива – вид центральной проекции
Перспектива – вид центральной проекции Строительное черчение
Строительное черчение Нанесение размеров на чертежах
Нанесение размеров на чертежах Проставление размеров на чертежах
Проставление размеров на чертежах Инженерная графика. Практика
Инженерная графика. Практика Метод архитектора. Методы построения перспективы: метод архитекторов
Метод архитектора. Методы построения перспективы: метод архитекторов