Содержание
- 2. Модели обработки остатков 2 Из исходного временного ряда yt исключаем всю неслучайную составля-ющую, в частности, тренд
- 3. Авторегрессия первого порядка. Марковский процесс AR(1) 3 Домножим на εt, εt–1, εt–2 и т.д. и перейдем
- 4. Авторегрессия второго порядка. Процесс Юла AR(2) 4 Итоговые формулы: ………………………………………………………………………………… Процесс Юла AR(2): Идентификация модели: найти
- 5. Авторегрессия порядка p: AR(p) 5 Итоговые формулы: Общий вид авторегрессионной модели AR(p): Идентификация модели: найти и
- 6. Модели скользящего среднего 6 Общий вид модели MA(q): Частные случаи: Двойственность в представлении моделей AR(p) и
- 7. Скользящее среднее первого порядка: MA(1) 7 Модель MA(1): Идентификация модели: найти и Выбираем из двух корней
- 8. Скользящее среднее порядка q: MA(q) 8 Модель MA(q): Идентификация модели: найти и Идентификация модели осуществляется с
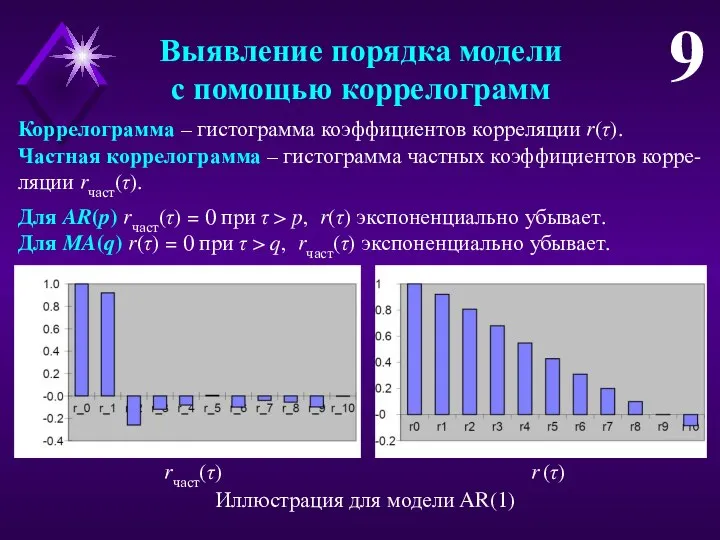
- 9. Выявление порядка модели с помощью коррелограмм 9 Коррелограмма – гистограмма коэффициентов корреляции r(τ). Частная коррелограмма –
- 10. Авторегрессионные модели со скользящими средними в остатках 10 Модель ARMA(p, q): Замечание: εt – не зависит
- 11. Авторегрессионные модели со скользящими средними в остатках 11 Этап 2: нахождение θ1,…,θq из системы нелинейных уравнений
- 12. Операторы F+ и F_ сдвига во времени 12 Оператор «вперед»: F+εt = εt+1; Оператор «назад»: F_εt
- 13. Проблема перепараметризации 13 Пример модели ARMA(2, 1): Можно ожидать нестабильность оценок параметров. Если сокращение на похожие
- 14. Проверка возможности упрощения модели ARMA(p,q) 14 Представление модели ARMA(p,q) в еще одной форме: zi (α) –
- 15. Многомерный временной ряд. Лаговые модели 15 Многомерный временной ряд: Можно учитывать лаг – запаздывание во времени.
- 16. Регрессионные модели с распределенными лагами 16 Проблемы использования обычных регрессионных моделей: 1. Неизвестен период распределенного во
- 17. Модель Койка 17 Предположения модели: Период распределенного во времени воздействия велик, в пределе ра-вен бесконечности. Сила
- 18. Полиномиальная лаговая структура Ширли Алмон 18 Предположения модели: Период распределенного во времени воздействия велик, в пределе
- 19. Полиномиальная лаговая структура Ширли Алмон 19 Большое число параметров (T+2) меняется на малое (m+2): α, α0,…,αm.
- 21. Скачать презентацию

















 Итоги реализации второго этапа биологизации земледелия в 2020 году на территории Белгородской области
Итоги реализации второго этапа биологизации земледелия в 2020 году на территории Белгородской области Пространственная организация экономики регионов
Пространственная организация экономики регионов Энергосбережение в сушильных установках
Энергосбережение в сушильных установках Организация процесса инвентаризации технических средств сетевой инфраструктуры предприятия
Организация процесса инвентаризации технических средств сетевой инфраструктуры предприятия Экономические системы. Подготовка к ЕГЭ. Обществознание
Экономические системы. Подготовка к ЕГЭ. Обществознание Социальный прогресс и развитие общества
Социальный прогресс и развитие общества Producent. Formy przedsiębiorstw
Producent. Formy przedsiębiorstw Низкоуглеродное развитие экономики России: прогнозы и вызовы
Низкоуглеродное развитие экономики России: прогнозы и вызовы Хозяйство Центрального Казахстана
Хозяйство Центрального Казахстана Товары и услуги. Производство
Товары и услуги. Производство Основные сферы жизни общества
Основные сферы жизни общества Безработица - спутник рыночной экономики
Безработица - спутник рыночной экономики Анализ зачетной работы. Макроэкономические процессы. Измерители экономики
Анализ зачетной работы. Макроэкономические процессы. Измерители экономики Теория поведения фирмы. (Лекция 4)
Теория поведения фирмы. (Лекция 4) Применение результатов космической деятельности в организациях и отраслях национальной экономики
Применение результатов космической деятельности в организациях и отраслях национальной экономики Alcohol use and burden for 195 countries and territories, 1990–2016
Alcohol use and burden for 195 countries and territories, 1990–2016 შესავალი კურსი მიკროეკონომიკაში ანტიტრასტული პოლიტიკა და რეგულაციები კვირა 11
შესავალი კურსი მიკროეკონომიკაში ანტიტრასტული პოლიტიკა და რეგულაციები კვირა 11 Формування фінансових джерел санації підприємства
Формування фінансових джерел санації підприємства Інфляція та грошові реформи
Інфляція та грошові реформи Информационные технологии в экономике
Информационные технологии в экономике Оптимальная стратегия интеграции Беларуси в новую экономику. Внешняя торговля Республики Беларусь
Оптимальная стратегия интеграции Беларуси в новую экономику. Внешняя торговля Республики Беларусь 1 Рынок жилья Уфы - осень 2011 Сеть Агентств Недвижимости «ЭКСПЕРТ» Городская База Недвижимости. - презентация
1 Рынок жилья Уфы - осень 2011 Сеть Агентств Недвижимости «ЭКСПЕРТ» Городская База Недвижимости. - презентация Основные макроэкономические показатели
Основные макроэкономические показатели Теория трансакционных издержек
Теория трансакционных издержек Генезис понятия «регион»
Генезис понятия «регион» Приоритетные направления деятельности отдела по взаимодействию с ОМСУ в 2018 году
Приоритетные направления деятельности отдела по взаимодействию с ОМСУ в 2018 году Формирование и организация использования средств производства
Формирование и организация использования средств производства Экспертные методы в инвестиционностроительной и эксплуатационной деятельности. Введение в предмет
Экспертные методы в инвестиционностроительной и эксплуатационной деятельности. Введение в предмет