Forecast combinations

Lecture Objectives

Introduce the idea and rationale for forecast averaging
Identify

Introduction

Usually, multiple forecasts are available to decision makers
Differences in

Introduction

Disadvantages of using a single forecasting model:
may contain misspecifications of

Outline of the lecture

What is a combination of forecasts?
The theoretical problem

Part I. What is a combination of forecasts?
General framework and notation
The forecast

General framework

Today (at time T) we want to forecast the

Notation

is the value of Y at time t (today is

Interpretation of loss function L(e)

Squared error loss (mean squared forecasting error:

A combined forecast is a weighted average of M forecasts:
The

Clarification: combining forecasting errors

Notice that since then

Hence, if weights sum to

Summary: what is the problem all about? (II)
We want to find

General problem of finding optimal forecast combination

Let:
u an (M

Issues and clarifications

Do weights have to sum to one?
If forecasts

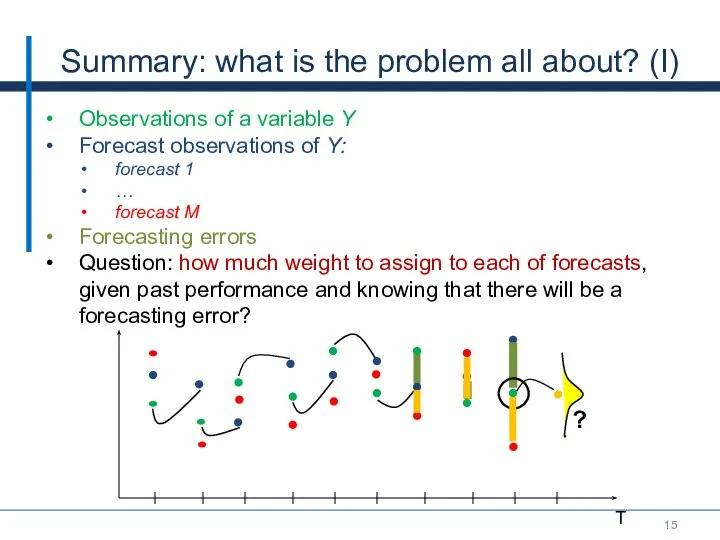
Summary: what is the problem all about? (I)

Observations of a variable

Part II. The theoretical problem and implementation issues
A simple example with only

Optimal weights in population (M = 2)

Result 1: The solution to

Interpreting the optimal weights in population

Consider the ratio of weights
A

Result: Forecast combination reduces
error variance

Compute the expected MSFE with the

Estimating Σ

The key ingredient for finding the optimal weights is

Issues with estimating Σ

Is the estimate of based on the

Optimality of equal weights

The simplest possible averaging scheme uses equal

Part III. Methods to estimate the weights:
M is small relative to

To combine or not to combine?

Assess if one forecast encompasses

OLS estimates of the optimal weights

Recall the general problem of

Reducing the dependency on sampling errors

Assume that estimate is affected

Part IV. Methods to estimate the weights: when M is large relative

Premise: problems with OLS weights

The problem with OLS weights:
If M

MSFE weights (or relative performance weights)

Relative performance weights

An alternative

Emphasizing recent performance

Compute:

where is the number of periods with δ(t)>0

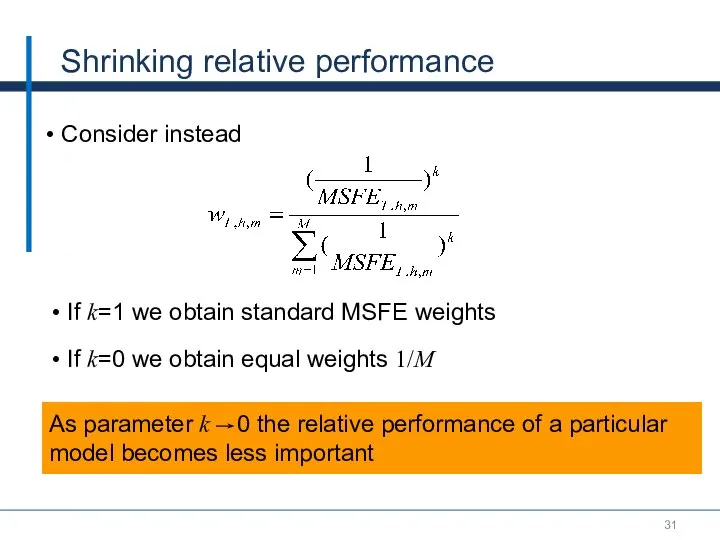
Shrinking relative performance

Consider instead

As parameter k 0 the relative performance

MSFE weights ignore correlations between forecasting errors
Ignoring it, when

Rank-based forecast combination

Aiolfi and Timmerman (2006) allow the weights to

Trimming

In forecast combination, it is often advantageous to discard models

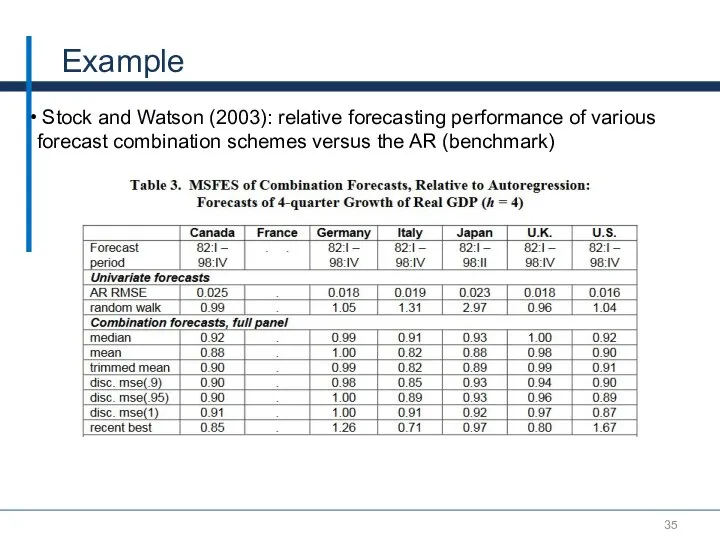
Example

Stock and Watson (2003): relative forecasting performance of various forecast

Part V. Improving the Estimates of the Theoretical Model Performance: Knowing the

Question

So far we assumed that we do not know models

Hansen (2007) approach

For a process yt there may be an

Hansen (2007) approach (2)

Let be the vector of T-h (in-sample!) residuals

Example of Hansen’s approach (M = 2)

We need to find

Conclusions – Key Takeaways

Combined forecasts imply diversification of risk (provided not

References

Aiolfi, Capistran and Timmerman, 2010, “Forecast Combinations“, in Forecast Handbook, Oxford,

Appendix

Appendix 1: generalization of problem 1

Let w be the (M x

Result 1: Let u be an (M x 1) vector of

Appendix 2: generalization of result 1

Let e be the (M x

Appendix 2: generalization of result 1 (M = 2)

Let Σt,h be

Optimal weights in population (M = 2)

Result 1: The solution to

Appendix 3

Notice that

Need to show that the following inequality holds

and that

Rearrange

Appendix 4: trading-off bias vs. variance

The MSFE loss function of

Appendix 4

The MSFE loss function of a forecast has two components:
the

Appendix 5

Suppose that where P is an (m x T) matrix,

Appendix 5

Consider:

Appendix 6: Adaptive weights

Relative performance weights may be sensitive to