Содержание
- 2. Классификация экономического прогнозирования В зависимости от периода упреждения :: Краткосрочное (прогноз делается на период от нескольких
- 3. Общие положения о временных рядах Опр. 4. Под временным рядом подразумевают наблюдаемую реализацию анализируемого случайного процесса,
- 4. Требования, предъявляемые к информации Сопоставимость достигается в результате одинакового подхода к наблюдениям на разных этапах формирования
- 5. Причины аномальности 1. ошибки измерения в ходе сбора данных. 2. отклонения, носящие объективный характер, но не
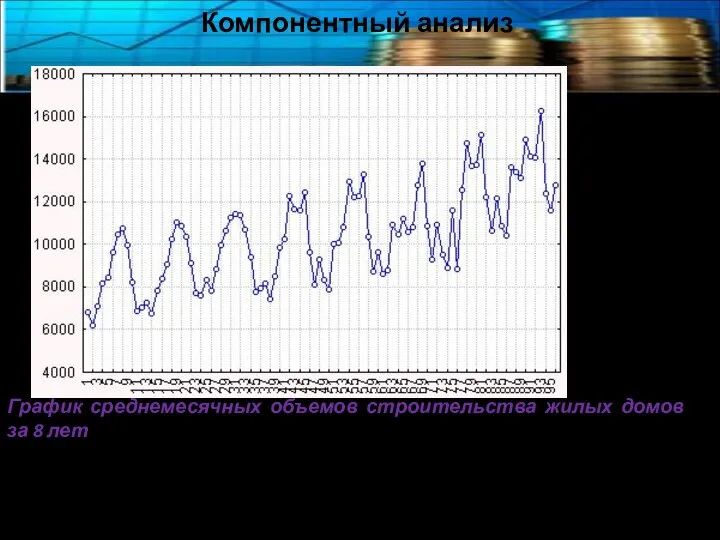
- 6. Компонентный анализ График среднемесячных объемов строительства жилых домов за 8 лет Можно увидеть ряд компонент: Тренд,
- 7. Тренд Пусть временной ряд можно представить в виде: Величина εt - абсолютно случайная составляющая, называемая белым
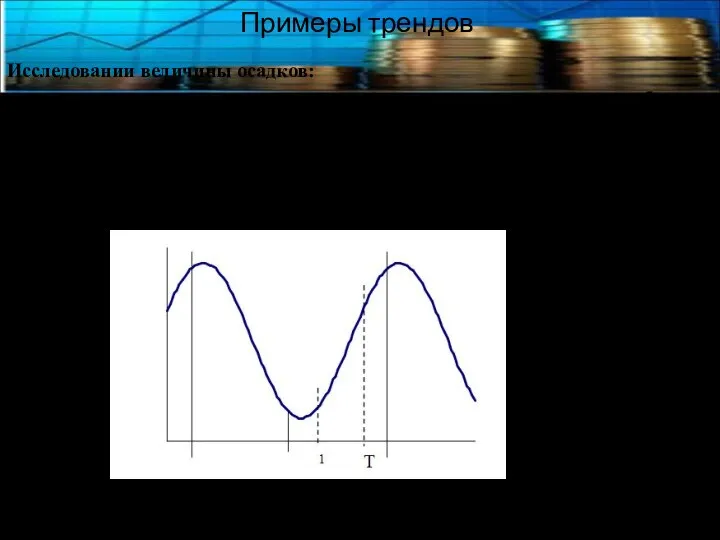
- 8. Примеры трендов Исследовании величины осадков: в течение ста лет медленное увеличение в течение всего периода может
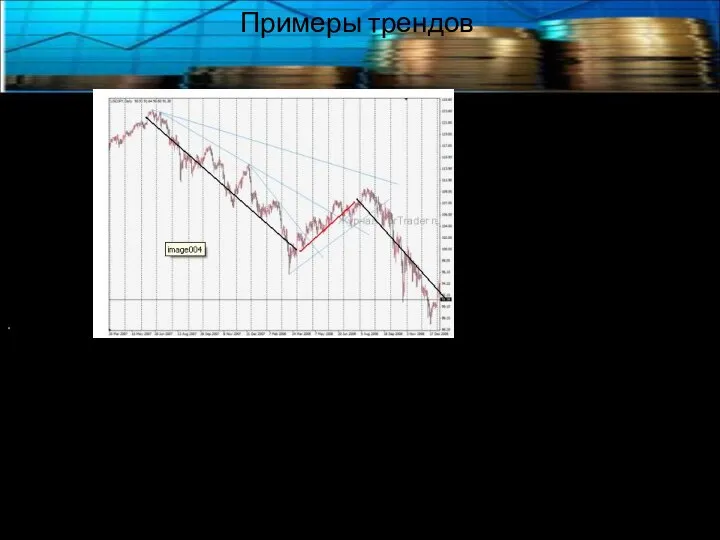
- 9. Примеры трендов . Кусочно-линейный тренд
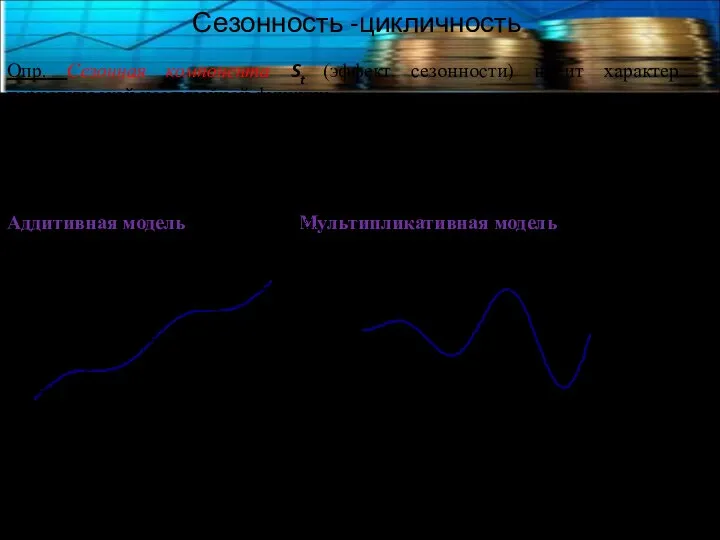
- 10. Сезонность -цикличность Опр. Сезонная компонента St (эффект сезонности) носит характер периодической неслучайной функции. Термин «сезонность» относят
- 11. Определение наличия тренда и сезонной компоненты Определения наличия тренда на основе: Визуального анализа графика исходных данных;
- 12. Что такое спектральный анализ? Ряд Фурье выглядит следующим образом: Длина периода членов ряда, следующая: первый синусоидальный
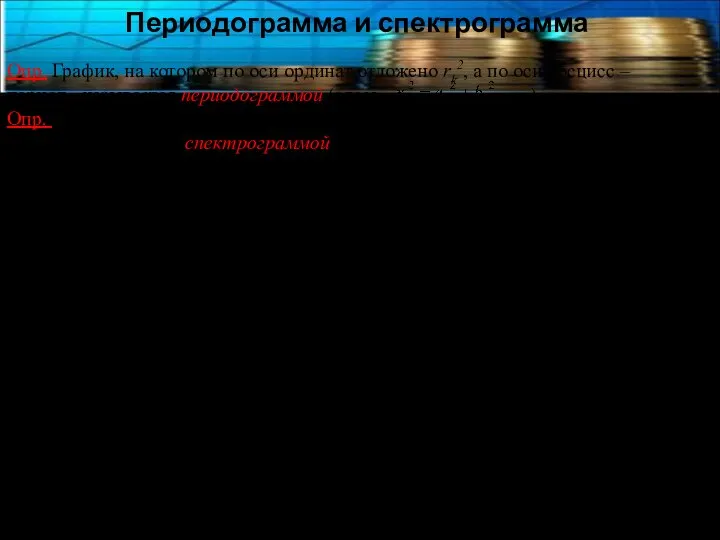
- 13. Периодограмма и спектрограмма Опр. График, на котором по оси ординат отложено rk2, а по оси абсцисс
- 14. Определение наличия периодической составляющей Если среднее значение временного ряда равно нулю (т.е. тренда нет), то выражение
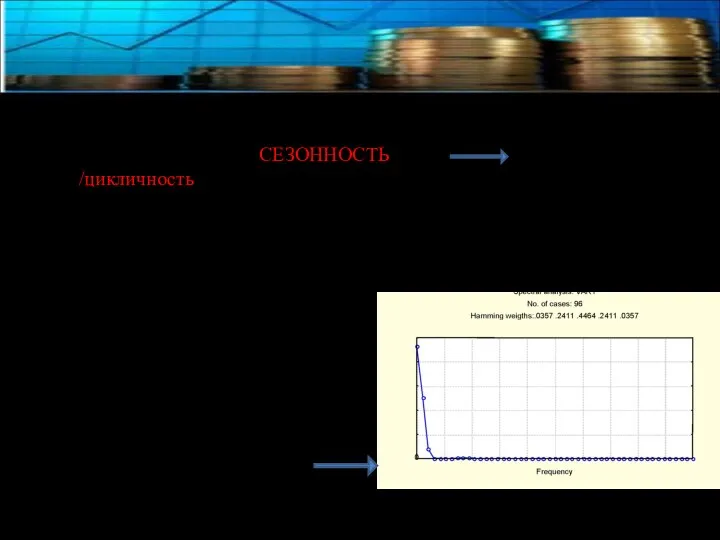
- 15. СЕЗОННОСТЬ /цикличность Периодограмма ряда, содержащего сезонную компоненту (с периодом 12) Спектрограмма ряда, содержащего тренд. Спектр будет
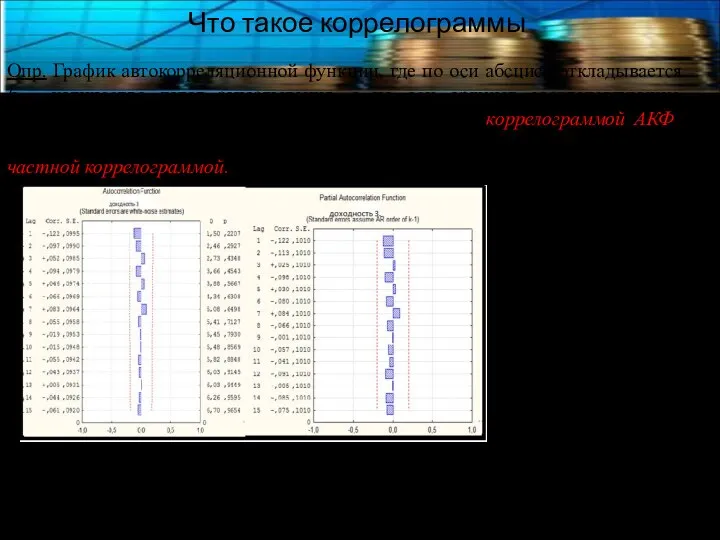
- 16. Что такое коррелограммы С помощью коэффициентов автокорреляции, можно измерить связь между текущими и прошлыми значениями исходного
- 17. Что такое коррелограммы Опр. График автокорреляционной функции, где по оси абсцисс откладывается k – количество лагов
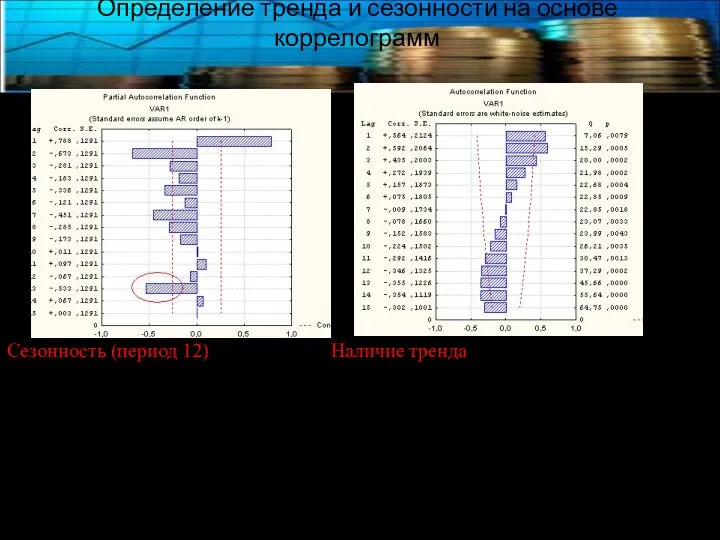
- 18. Определение тренда и сезонности на основе коррелограмм Сезонность (период 12) Наличие тренда
- 19. Адаптивные модели прогнозирования Опр Адаптивными методами прогнозирования (или моделями экспоненциального сглаживания) называется методы, позволяющие строить самокорректирующиеся
- 20. Линейная модель Брауна Где - прогноз, выполненный на τ шагов вперед на t-м шаге адаптации, -
- 21. Расчет экспоненциальных средних Экспоненциальная средняя 1- го порядка: где β – параметр сглаживания, или так называемый
- 22. Начальные значения Начальные значения экспоненциальных средних Начальные значения параметров рассчитываются как коэффициенты регрессии .
- 23. Выбор параметра адаптации Значение параметра адаптации β=1-α лежит в интервале (1; 0). Если требуется придать вес
- 24. Квадратичная модель Брауна Где - прогноз, выполненный на τ шагов вперед на t-м шаге адаптации, -
- 25. Расчет экспоненциальных средних Экспоненциальные средние: Расчет начальных значений экспоненциальных средних:
- 26. Модель Хольта где - прогноз, выполненный на τ шагов вперед после t шагов адаптации, - корректируемые
- 27. мультипликативная модель Хольта-Уинтерса Рекуррентные формулы обновления : где - адаптируемые параметры линейного тренда на t-м шаге
- 28. аддитивная модель Хольта-Уинтерса Рекуррентные формулы обновления : где - адаптируемые параметры линейного тренда на t-м шаге
- 30. Скачать презентацию

















 Types and Forms of Business
Types and Forms of Business Отчет о проектах и деятельности Агентства 2017
Отчет о проектах и деятельности Агентства 2017 Поняття, функції, задачі та правові основи діяльності ОПЕК.
Поняття, функції, задачі та правові основи діяльності ОПЕК. Первые эмпирические обобщения в истории экономики
Первые эмпирические обобщения в истории экономики Ценообразование в условиях монополии
Ценообразование в условиях монополии Инновационные показатели, международная оценка инноваций и ранжирование
Инновационные показатели, международная оценка инноваций и ранжирование Заработная плата и безработица
Заработная плата и безработица Презентация Финансы экономических субъектов
Презентация Финансы экономических субъектов Безработица
Безработица Кадастровая стоимость и нормативная цена земли
Кадастровая стоимость и нормативная цена земли Министерство сельского хозяйства Российской Федерации
Министерство сельского хозяйства Российской Федерации Рынки факторов производства
Рынки факторов производства Общественный сектор. Экономика общественного сектора
Общественный сектор. Экономика общественного сектора Последствия Великих географических открытий
Последствия Великих географических открытий Теория затрат
Теория затрат Экономическая теория
Экономическая теория Повышение регулирующей роли государства в экономике ведущих стран мира в межвоенный период
Повышение регулирующей роли государства в экономике ведущих стран мира в межвоенный период Традиционная экономическая система
Традиционная экономическая система Микроэкономика часть 1. Доход и прибыль фирмы
Микроэкономика часть 1. Доход и прибыль фирмы Роль государства в антикризисном управлении. (Тема 3)
Роль государства в антикризисном управлении. (Тема 3) Внешние эффекты (экстерналии)
Внешние эффекты (экстерналии) Цифровая экономика и ФинТех: новая стратегия и культура
Цифровая экономика и ФинТех: новая стратегия и культура Детский образовательный центр «Умный Совёнок»
Детский образовательный центр «Умный Совёнок» Международные экономические организации
Международные экономические организации ҚазақстанРеспубликасы президент Н. Назарбаевтың Қазақстан халқына жолдауы
ҚазақстанРеспубликасы президент Н. Назарбаевтың Қазақстан халқына жолдауы Размещение производительных сил
Размещение производительных сил Презентация по экономике ТИПЫ БЕЗРАБОТИЦЫ
Презентация по экономике ТИПЫ БЕЗРАБОТИЦЫ Социальное государство. Понятие, признаки , функции, модели
Социальное государство. Понятие, признаки , функции, модели