Содержание
- 2. 1. Основы теории биномиального распределения Пусть производится серия из n независимых опытов, в каждом из которых
- 3. 1. Основы теории биномиального распределения Здесь pk - вероятность того, что событие A появится ровно k
- 4. 2. Пример решения задачи Задание. Студент может получить пятерку на экзамене с вероятностью 60%. Найти ряд
- 5. 2. Пример решения задачи Решение. 1) Пусть событие «A= студент получил 5 на экзамене»; Тогда: и
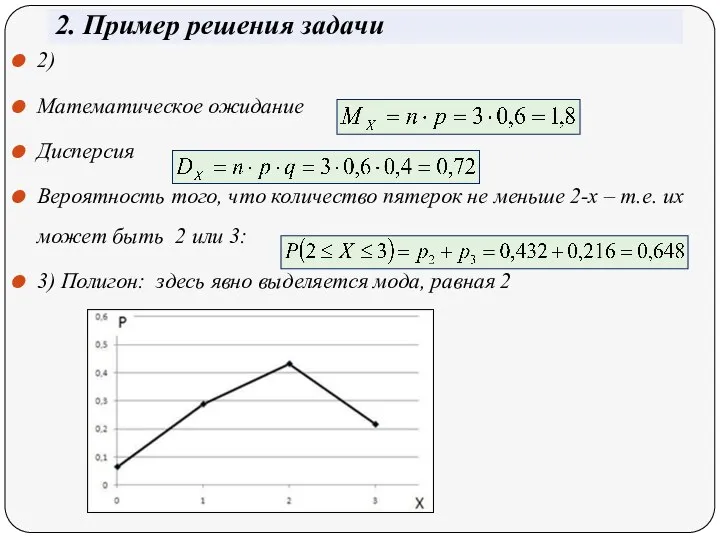
- 6. 2. Пример решения задачи 2) Математическое ожидание Дисперсия Вероятность того, что количество пятерок не меньше 2-х
- 7. 2. Пример решения задачи 3) Функция распределения: Таблица значений функции распределения:
- 9. Скачать презентацию





 Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Дифракція світла. Принцип Гюйгенса-Френеля. Дифракційні картини
Дифракція світла. Принцип Гюйгенса-Френеля. Дифракційні картини Классификация и основные виды антенн. Антенно-фидерные устройства и распространение радиоволн
Классификация и основные виды антенн. Антенно-фидерные устройства и распространение радиоволн Точка росы
Точка росы Состав вещества. Смеси
Состав вещества. Смеси Физика для малышей
Физика для малышей Конструкция беспилотного летательного аппарата
Конструкция беспилотного летательного аппарата Газонаполненные детекторы
Газонаполненные детекторы Электрогенератор. Функции
Электрогенератор. Функции Особенности заданий ЕГЭ. Электромагнитные колебания и волны
Особенности заданий ЕГЭ. Электромагнитные колебания и волны Основы электрокардиографии и реографии. Электродиагностика. Электротерапия
Основы электрокардиографии и реографии. Электродиагностика. Электротерапия Рычаг и блок
Рычаг и блок Презентация по физике "Постійні магніти" - скачать бесплатно
Презентация по физике "Постійні магніти" - скачать бесплатно Лазер и его применение
Лазер и его применение Объём тела
Объём тела «Волшебный мир магнетизма» Школкина Людмила Александровна Учитель физики МОБУ СОШ № 24 имени С. И. Климакова Г. Якутск
«Волшебный мир магнетизма» Школкина Людмила Александровна Учитель физики МОБУ СОШ № 24 имени С. И. Климакова Г. Якутск Конденсаторы. 10 класс
Конденсаторы. 10 класс Определение твердости
Определение твердости Трансформаторы. Принцип действия
Трансформаторы. Принцип действия Теоретические основы теплотехники
Теоретические основы теплотехники Аксиально-поршневые гидромашины. (Лекция 5)
Аксиально-поршневые гидромашины. (Лекция 5) Характеристика гидропривода. Классификация гидропривода. Преимущества и недостатки гидропривода. (Лекция 1)
Характеристика гидропривода. Классификация гидропривода. Преимущества и недостатки гидропривода. (Лекция 1) Открытие нейтрона. Строение атомного ядра.
Открытие нейтрона. Строение атомного ядра. Презентация по физике Динамика часть 3
Презентация по физике Динамика часть 3 Реактивное движение
Реактивное движение Презентация Применение кристаллов
Презентация Применение кристаллов  Динамика. Законы динамики
Динамика. Законы динамики Нагрев материалов лазерным излучением
Нагрев материалов лазерным излучением