Содержание
- 2. Быстрое преобразование Фурье Основной принцип всех этих алгоритмов заключается в разложении операций вычисления ДПФ сигнала длины
- 3. Быстрое преобразование Фурье Рассмотрим алгоритмы БПФ с основанием 2, когда длина последовательности , где целое число.
- 4. Быстрое преобразование Фурье Разобьем на две -точечные последовательности, состоящие из отсчетов с четными и нечетными номерами
- 5. Быстрое преобразование Фурье Так как , то предыдущее выражение можно записать в виде: (12.1) Каждая из
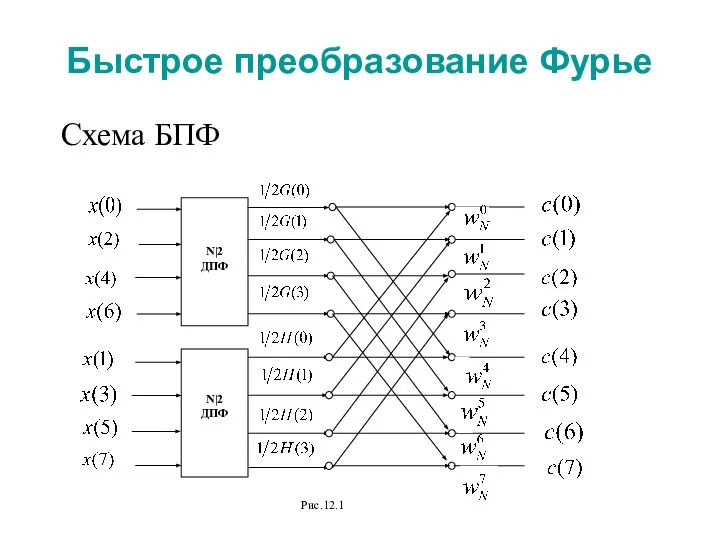
- 6. Быстрое преобразование Фурье Схема БПФ
- 7. Быстрое преобразование Фурье Далее можно вычислить каждое точечное ДПФ разбиением сумм на два точечных ДПФ. Таким
- 8. Быстрое преобразование Фурье Продолжим описанную процедуру разбиения исходной ДПФ на преобразования меньшей размерности, пока не останутся
- 9. Быстрое преобразование Фурье Число требуемых при этом пар операций «умножение – сложение» можно оценить как .
- 10. Быстрое преобразование Фурье Из рассмотренного алгоритма следует, что на каждой ступени вычислений происходит преобразование одного множества
- 12. Скачать презентацию








 Что такое Тензорезистор
Что такое Тензорезистор Экзамен по электротехнике
Экзамен по электротехнике Элементы механики жидкости. Давление в жидкости и газе
Элементы механики жидкости. Давление в жидкости и газе Геофизические исследования скважин
Геофизические исследования скважин Процессоры. Виды процессоров
Процессоры. Виды процессоров Что такое минералы
Что такое минералы Резерфорд тәжірбесі. Атомның планетарлық моделі
Резерфорд тәжірбесі. Атомның планетарлық моделі Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью Механические колебания
Механические колебания Физические основы механики. Динамика. Лекция 1.2
Физические основы механики. Динамика. Лекция 1.2 Агрегатные состояния вещества
Агрегатные состояния вещества Молекулярная физика
Молекулярная физика  Количество теплоты
Количество теплоты Индуктивность. Соединения индуктивностей
Индуктивность. Соединения индуктивностей Стабилитрон тақырыбына арналған презентация
Стабилитрон тақырыбына арналған презентация Презентация по физике Основные понятия кинематики. Виды движения. Преобразование координат Галилея.
Презентация по физике Основные понятия кинематики. Виды движения. Преобразование координат Галилея.  Методы получения резьбовых соединений
Методы получения резьбовых соединений Закон всемирного тяготения. Искусственные спутники Земли. Решение задач
Закон всемирного тяготения. Искусственные спутники Земли. Решение задач Основные параметры элементов электрической цепи
Основные параметры элементов электрической цепи Обзор теорий электрического пробоя твердых диэлектриков Выполнил студент группы 5А1В Зубков А.В. Проверил преподаватель Мыт
Обзор теорий электрического пробоя твердых диэлектриков Выполнил студент группы 5А1В Зубков А.В. Проверил преподаватель Мыт Механические волны. Звук. (Лекция 2)
Механические волны. Звук. (Лекция 2) Работа и мощность
Работа и мощность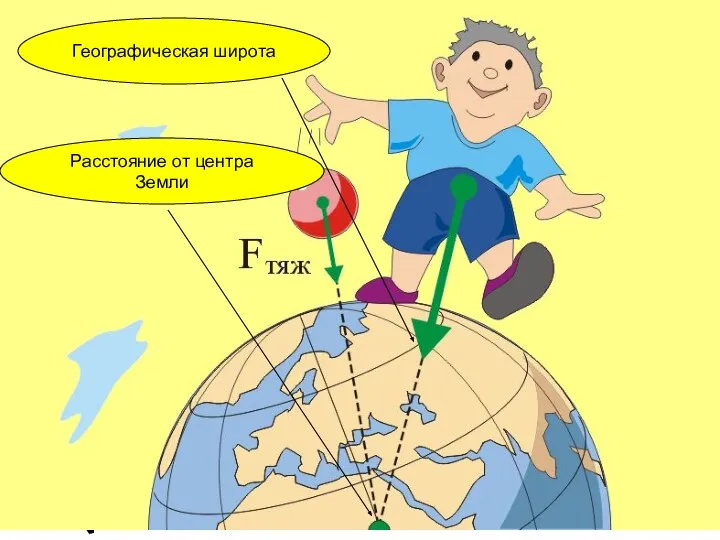 Закон всемирного тяготения
Закон всемирного тяготения Общая энергетика
Общая энергетика Энергия движения твёрдого тела
Энергия движения твёрдого тела Физика конденсированного состояния. Гетеропереходы
Физика конденсированного состояния. Гетеропереходы Электрическая система. (Лекция 1)
Электрическая система. (Лекция 1) Электромагнитные поля
Электромагнитные поля