Содержание
- 2. 10-18 10-15 10-12 10-9 10-6 10-3 100 103 106 109 1012 1015 1018 1021 10-21 10-24
- 3. . ФИЗИКА – способ познания мира, с помощью эксперимента, здравого смысла и логики ВАЖНО! Физика начинается
- 4. . ФИЗИКА – способ познания мира, с помощью эксперимента, здравого смысла и логики ВАЖНО! Физика начинается
- 5. . Понятия и математические инструменты, необходимые, чтобы начать изучать физику Concepts and Mathematical Tools, necessary to
- 6. Цифры и числа Позиционную десятичную систему счисления, которую мы привычно используем сегодня изобрели в Индии, в
- 7. Умение считать в уме, быстро и приближенно, абсолютно необходимо и инженеру, и физику! Картина Н.П. Богданова-Бельского
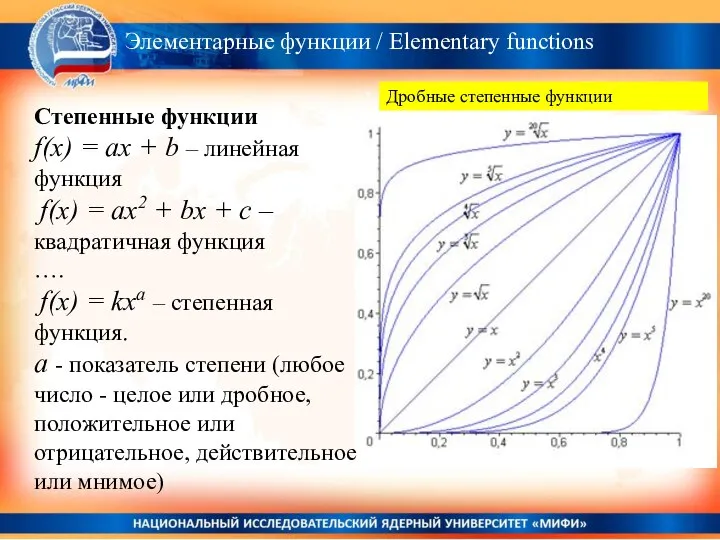
- 8. . Степенные функции f(x) = ax + b – линейная функция f(x) = ax2 + bx
- 9. Элементарные функции / Elementary functions . Степенные функции f(x) = ax + b – линейная функция
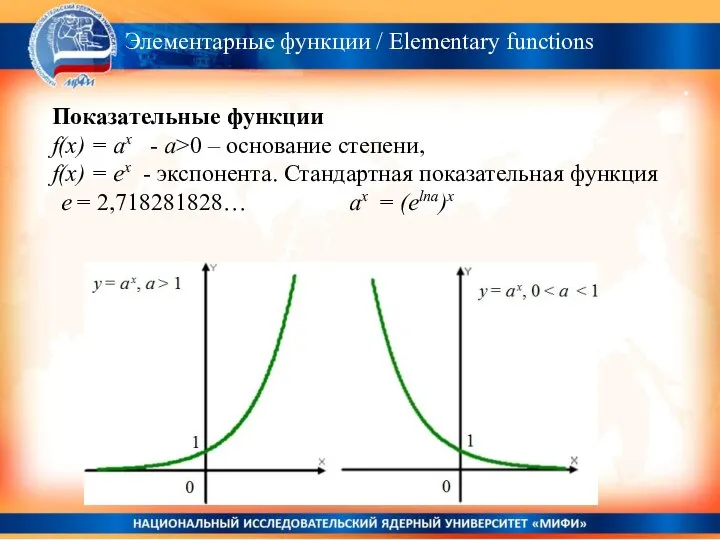
- 10. . Показательные функции f(x) = аx - а>0 – основание степени, f(x) = ex - экспонента.
- 11. . Логарифмы Если x = ay, то y = logаx f(x) = logаx - а (>0)
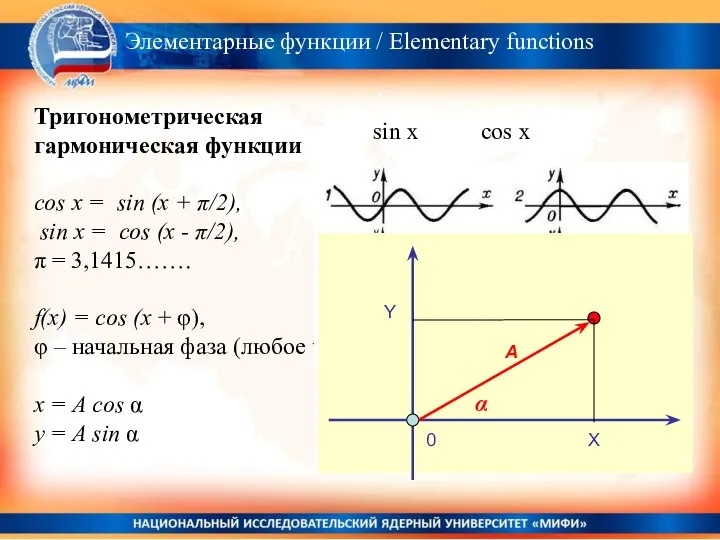
- 12. . Тригонометрическая гармоническая функции cos x = sin (x + π/2), sin x = cos (x
- 13. . Другие тригонометрические функции tg x = sin x / cos x; ctg x = cos
- 14. . Тригонометрические формулы sin(a+b) = sin(a)cos(b) + cos(a)sin(b) => sin(2a) = 2sin(a)cos(a) cos(a+b) = cos(a)cos(b) –
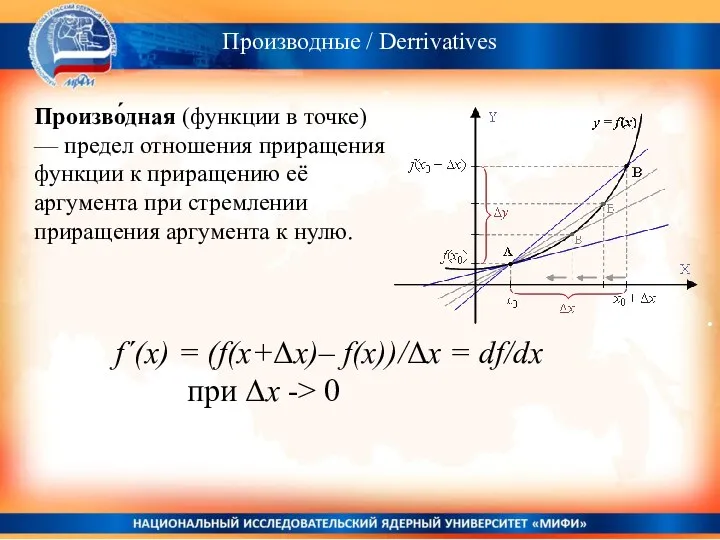
- 15. . Произво́дная (функции в точке) — предел отношения приращения функции к приращению её аргумента при стремлении
- 16. Производные / Derrivatives
- 17. Первообразные / Anti-derivatives f(x) = F'(x) Функция f(x) есть (=) производная (‘) от функции F(x) F(x)
- 18. Первообразные / Anti-derivatives F(x) = ∫ f(x)dx Функция F(x) есть (=) первообразная (∫dx) от функции f(x)
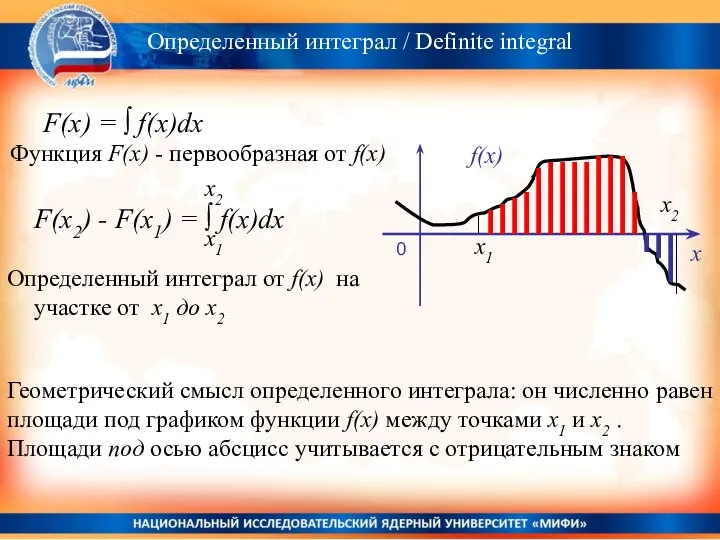
- 19. Определенный интеграл / Definite integral F(x) = ∫ f(x)dx Функция F(x) - первообразная от f(x) F(x2)
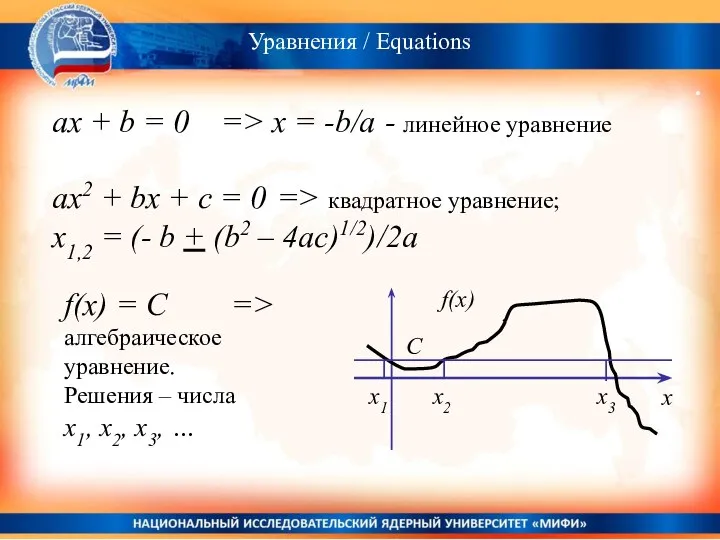
- 20. . ax + b = 0 => x = -b/a - линейное уравнение ax2 + bx
- 21. f(x) = С - алгебраическое уравнение. Решения - числа G(x) = af (x)+ bf´(x) + cf´´(x)
- 22. Isaac Newton Сэр Айзек Ньютон (Isaac Newton, 1643-1727) и его главный труд - «Натуральная Философия и
- 23. Физика до Ньютона Общая теория движения (механика) Аристотеля: Движения бывают естественные (не требующие для объяснения никакой
- 24. Физика до Ньютона Общая теория движения (механика) Аристотеля: Все остальные виды движений требуют или постоянного приложения
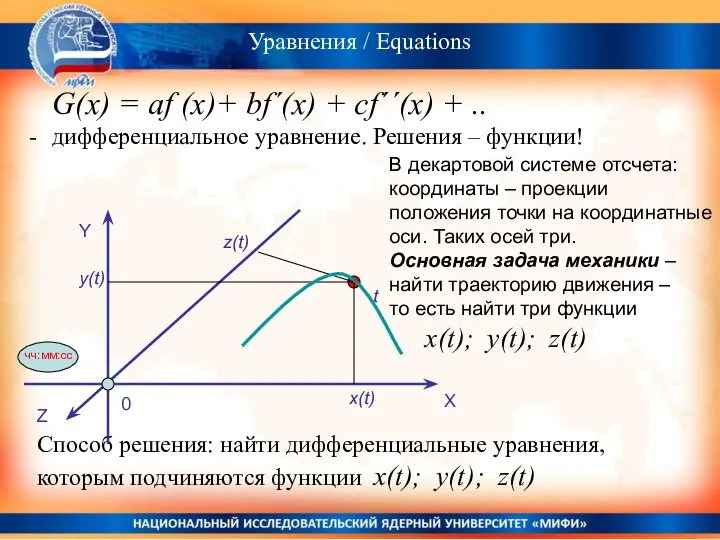
- 25. G(x) = af (x)+ bf´(x) + cf´´(x) + .. дифференциальное уравнение. Решения – функции! Уравнения /
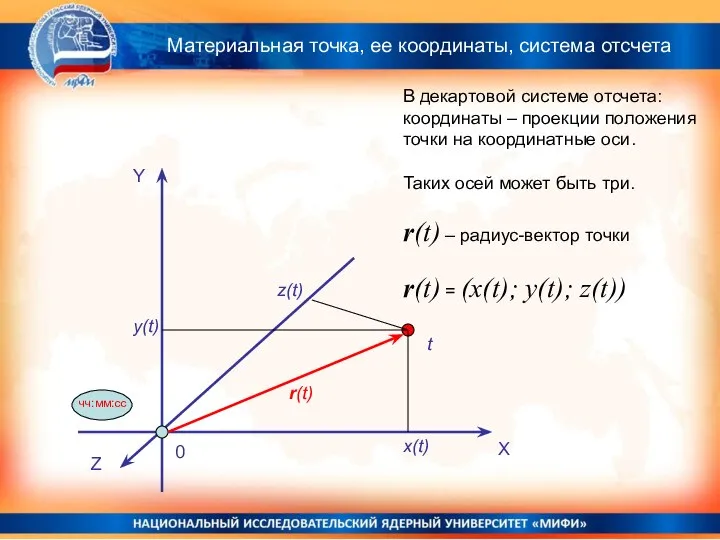
- 26. Материальная точка, ее координаты, система отсчета Y X Z z(t) y(t) x(t) 0 чч:мм:сс t В
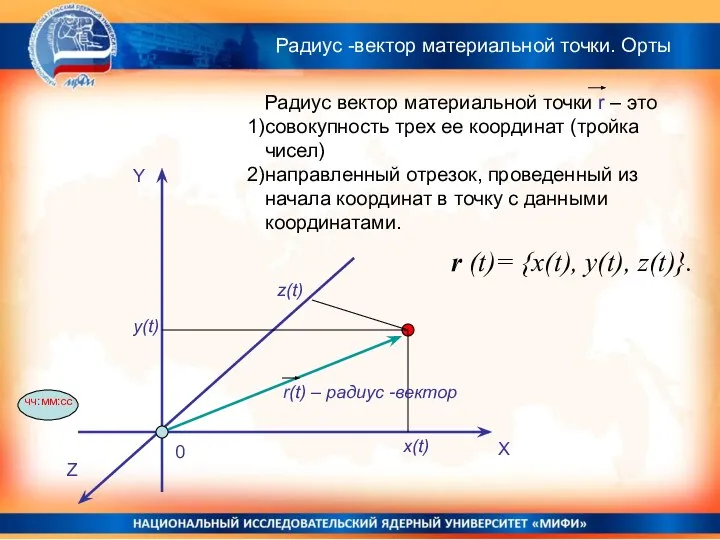
- 27. Радиус -вектор материальной точки. Орты Радиус вектор материальной точки r – это совокупность трех ее координат
- 28. a Геометрический подход: Вектор = направленный отрезок, который Имеет абсолютную величину (модуль) и направление. Важно: параллельные
- 29. Алгебраический подход: вектор = упорядоченная группа (тройка) чисел. Удобнее всего определить вектор через его проекции на
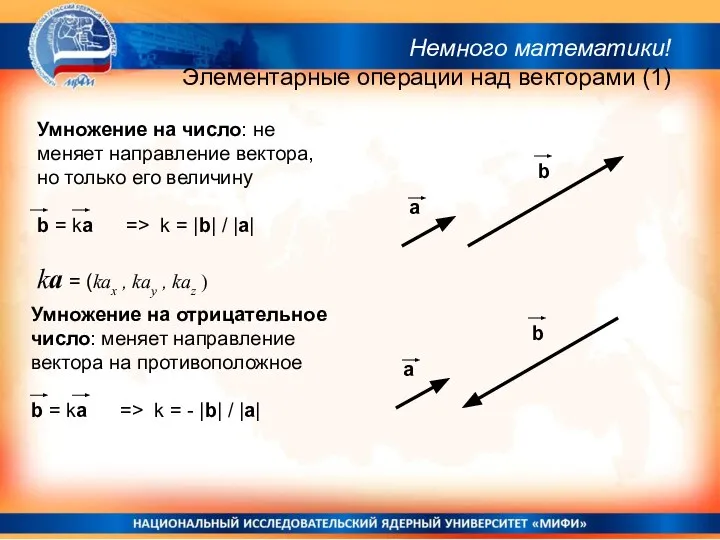
- 30. Умножение на число: не меняет направление вектора, но только его величину b = ka => k
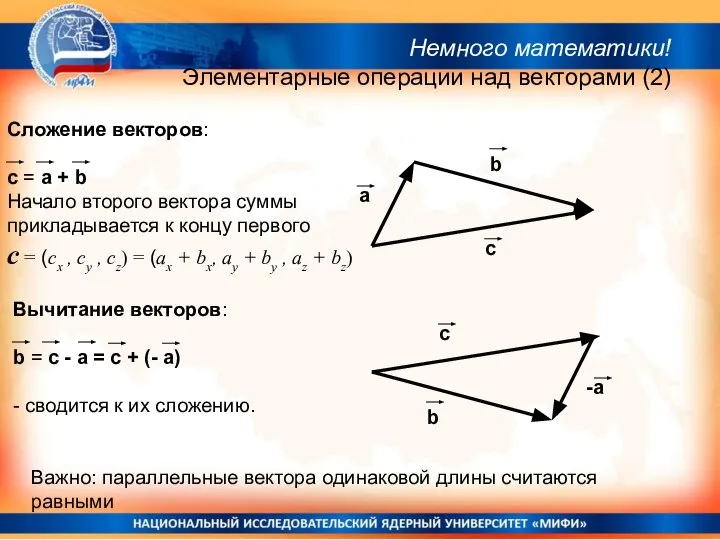
- 31. Сложение векторов: c = a + b Начало второго вектора суммы прикладывается к концу первого c
- 32. Вектора определяются своими координатами : a = {ax, ay, az}; b = {bx, by, bz}; Скалярное
- 33. Размерности физических величин Почти каждая физическая величина имеет ту или иную размерность, и соответствующую единицу измерения.
- 34. Системы физических величин Разные единицы удобны для измерений в разных масштабах и/или традиционно применяются в разных
- 35. Системы физических величин В основе системы SI - три базовые единицы измерения длины [l] – метр
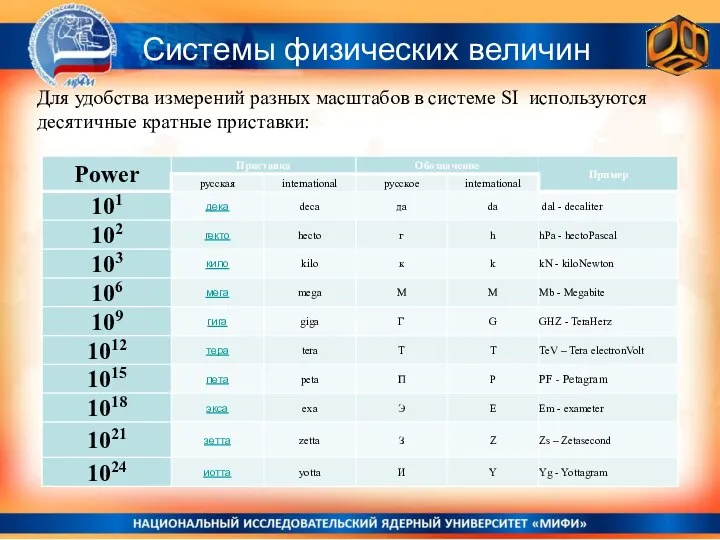
- 36. Системы физических величин Для удобства измерений разных масштабов в системе SI используются десятичные кратные приставки:
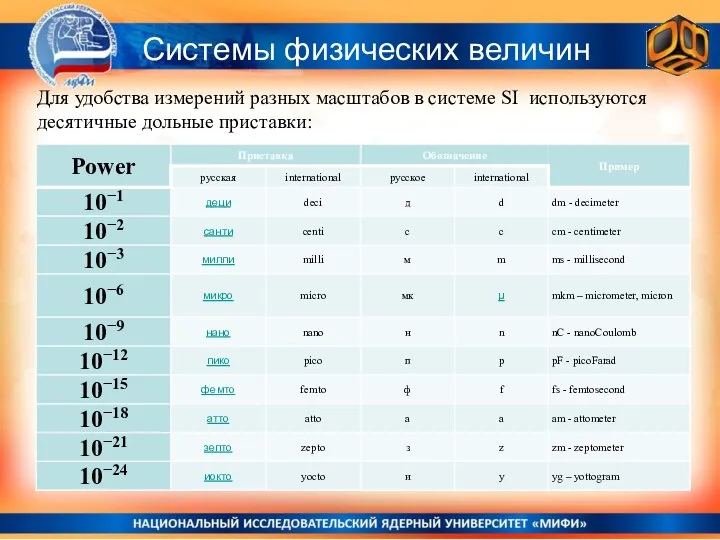
- 37. Системы физических величин Для удобства измерений разных масштабов в системе SI используются десятичные дольные приставки:
- 38. Размерности физических величин Сравнивать разноразмерные величины – бессмысленно. Что больше: 6 секунд или 3 метра -
- 39. Оценить (примерно) период колебаний (1) математического маятника и (2) пружинного маятника, не применяя законов Ньютона Параметры:
- 40. Оценить (примерно) период колебаний (1) математического маятника и (2) пружинного маятника, не применяя законов Ньютона Параметры:
- 41. Оценить (примерно) период колебаний (1) математического маятника и (2) пружинного маятника, не применяя законов Ньютона Параметры:
- 42. Мg[кг*м/с2] ~ ρ[кг/м3]S2[м4]v2[1/с2] => M ~ 1,3* 102*102/10 ~ 103 кг~ 1т «Хороший физик, до того,
- 43. Физические основы механики Лекция 01 Спасибо за внимание! Курс общей физики НИЯУ МИФИ
- 45. Скачать презентацию



























![Мg[кг*м/с2] ~ ρ[кг/м3]S2[м4]v2[1/с2] => M ~ 1,3* 102*102/10 ~ 103 кг~](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/623663/slide-41.jpg)

 Полупроводники
Полупроводники Материя. Движение. Время. Пространство. Взаимодействия
Материя. Движение. Время. Пространство. Взаимодействия Теплопроводность газов
Теплопроводность газов Теория фотоэффекта
Теория фотоэффекта Напряженность электрического поля Электрическое напряжение
Напряженность электрического поля Электрическое напряжение Спектральный анализ
Спектральный анализ Методи розрахунку електричних кіл постійного струму
Методи розрахунку електричних кіл постійного струму Спроектировать участок механической обработки детали Рейка зубчатая
Спроектировать участок механической обработки детали Рейка зубчатая Комбинации приборов для Lada
Комбинации приборов для Lada Масса тела
Масса тела Презентация по физике "Излучение и спектры" - скачать
Презентация по физике "Излучение и спектры" - скачать  Ременные передачи. Виды, геометрия и кинематика. Расчет ременных передач. Лекция 1
Ременные передачи. Виды, геометрия и кинематика. Расчет ременных передач. Лекция 1 Аттестационная работа. Методическая разработка проекта по физике на тему «Сила трения и движение»
Аттестационная работа. Методическая разработка проекта по физике на тему «Сила трения и движение» Термодинамическая картина мира
Термодинамическая картина мира Постоянный электрический ток. Причины электрического тока
Постоянный электрический ток. Причины электрического тока Внутренняя энергия и способы ее изменения
Внутренняя энергия и способы ее изменения Водородный трамвай
Водородный трамвай Оценка материалов инженерно-геологических изысканий и их влияние на выбор конструкции фундаментов и метод производства работ
Оценка материалов инженерно-геологических изысканий и их влияние на выбор конструкции фундаментов и метод производства работ Урок-игра обобщающего повторения и контроля знаний по теме «Тепловые явления» (8 класс)
Урок-игра обобщающего повторения и контроля знаний по теме «Тепловые явления» (8 класс) Цифровая лаборатория по физике
Цифровая лаборатория по физике Механические колебания
Механические колебания Физика 11 класс «Оптические приборы»
Физика 11 класс «Оптические приборы» Звуковой резонанс
Звуковой резонанс Основне рівняння молекулярно-кінетичної теорії газів
Основне рівняння молекулярно-кінетичної теорії газів  Automaty a regularní výrazy. (Lekce 3)
Automaty a regularní výrazy. (Lekce 3) Презентация по физике "Виды электростанций" - скачать
Презентация по физике "Виды электростанций" - скачать  Открытие дисперсии и дифракции (оптика второй половины xvii века)
Открытие дисперсии и дифракции (оптика второй половины xvii века) Нефть
Нефть