Содержание
- 2. Bryła sztywna Układ cząstek w którym odległości między cząstkami nie zmieniają się w czasie. Jeżeli położenie
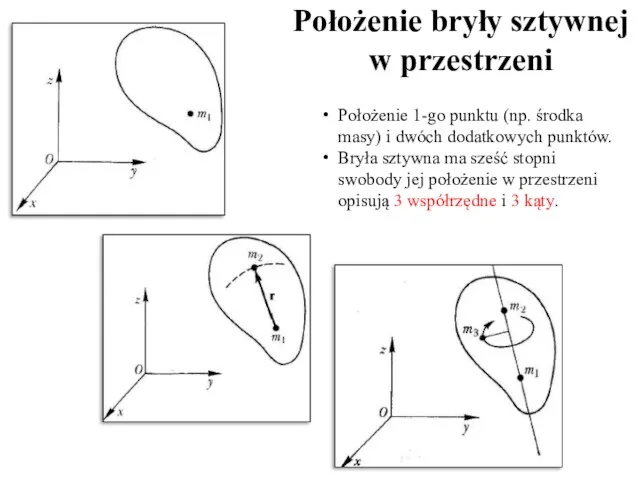
- 3. Położenie bryły sztywnej w przestrzeni Położenie 1-go punktu (np. środka masy) i dwóch dodatkowych punktów. Bryła
- 4. Bryła sztywna może poruszać się ruchem postępowym. Wtedy wektory prędkości są takie same dla wszystkich punktów
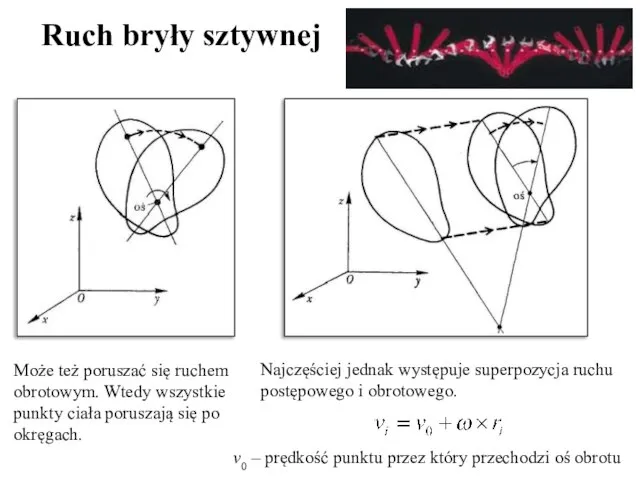
- 5. Może też poruszać się ruchem obrotowym. Wtedy wszystkie punkty ciała poruszają się po okręgach. Ruch bryły
- 6. Długość Kąt co daje: Położenie kątowe: prędkość kątowa: przyspieszenie kątowe: Przesunięcie kątowe, prędkość i przyspieszenie kątowe
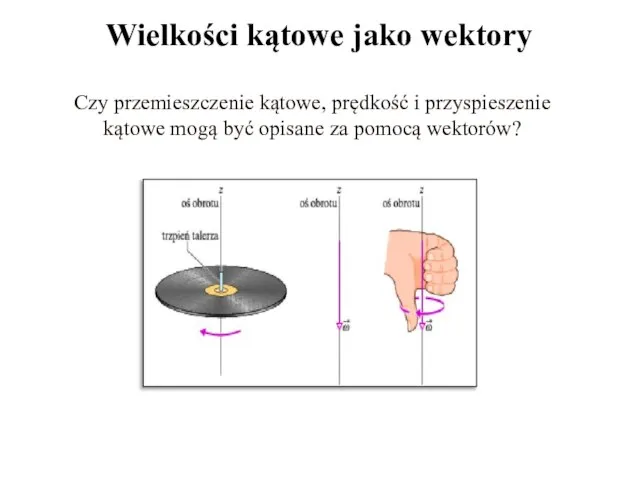
- 7. Czy przemieszczenie kątowe, prędkość i przyspieszenie kątowe mogą być opisane za pomocą wektorów? Wielkości kątowe jako
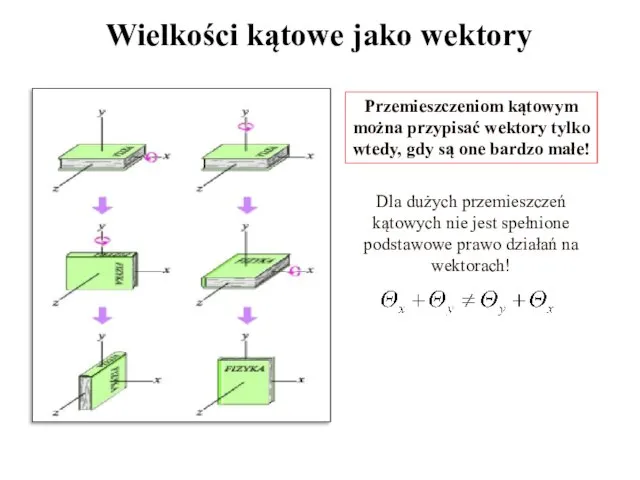
- 8. Przemieszczeniom kątowym można przypisać wektory tylko wtedy, gdy są one bardzo małe! Wielkości kątowe jako wektory
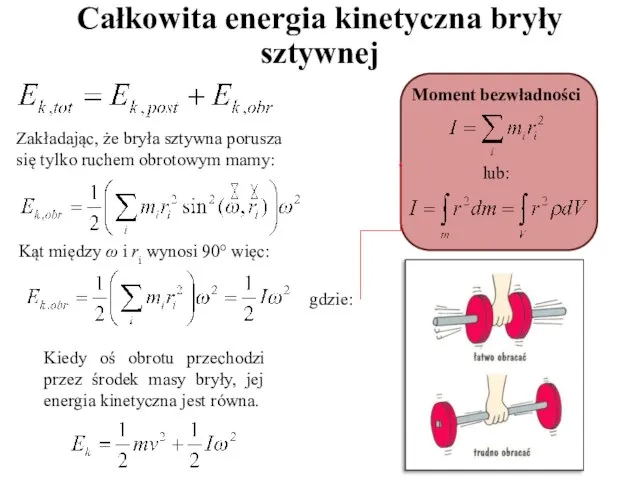
- 9. Całkowita energia kinetyczna bryły sztywnej energia kinetyczna ruchu postępowego bryły energia kinetyczna ruchu obrotowego bryły energia
- 10. Całkowita energia kinetyczna bryły sztywnej Zakładając, że bryła sztywna porusza się tylko ruchem obrotowym mamy: Kąt
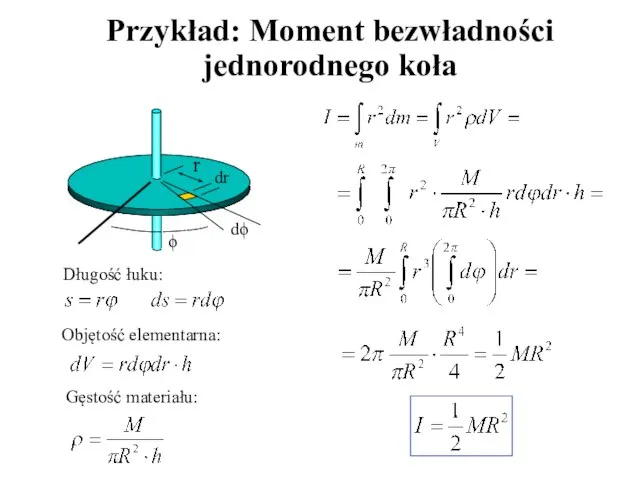
- 11. Przykład: Moment bezwładności jednorodnego koła Długość łuku: Objętość elementarna: Gęstość materiału:
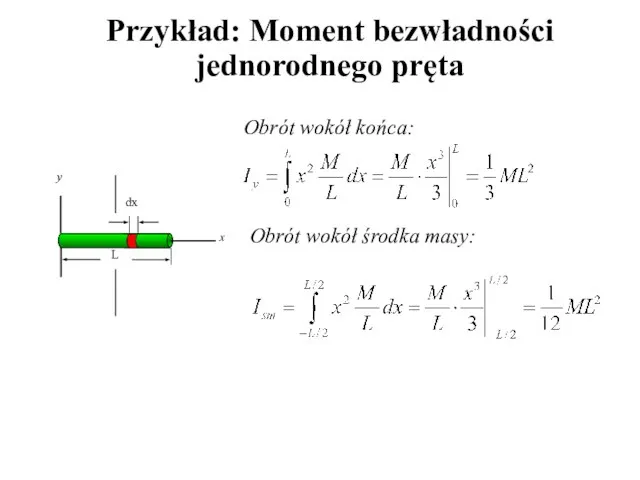
- 12. Obrót wokół końca: Obrót wokół środka masy: Przykład: Moment bezwładności jednorodnego pręta
- 13. Twierdzenie Steinera
- 14. Moment bezwładności względem osi przechodzącej przez środek masy: Odległość między osiami: Zgodnie z twierdzeniem Steinera: Moment
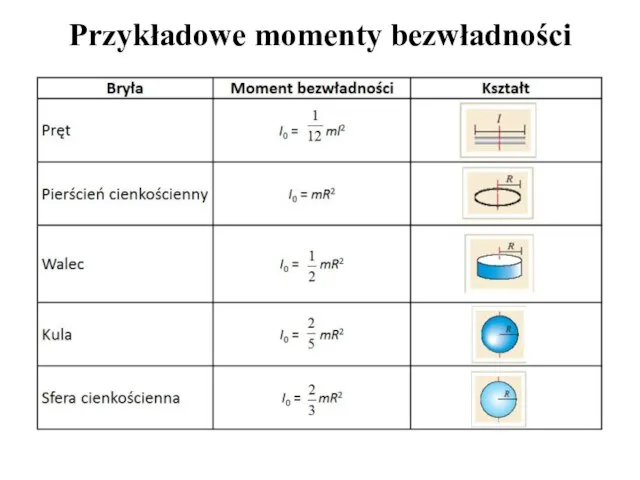
- 15. Przykładowe momenty bezwładności
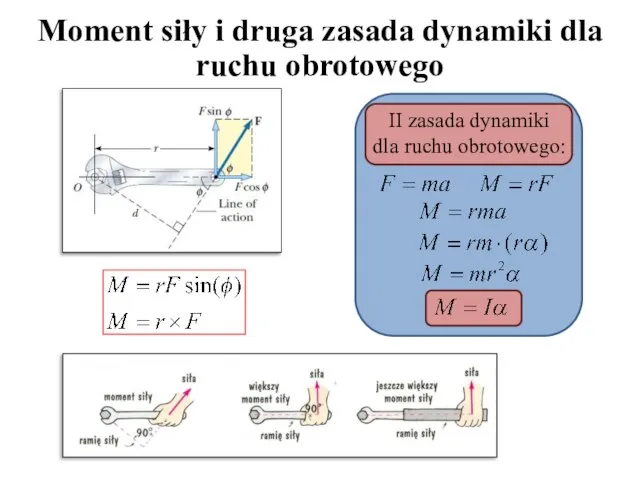
- 16. Moment siły i druga zasada dynamiki dla ruchu obrotowego II zasada dynamiki dla ruchu obrotowego:
- 17. Praca i moc w ruchu obrotowym Moc Praca:
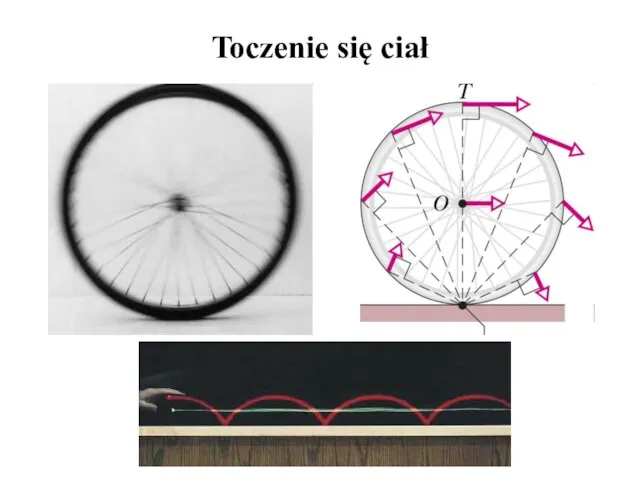
- 18. Toczenie się ciał
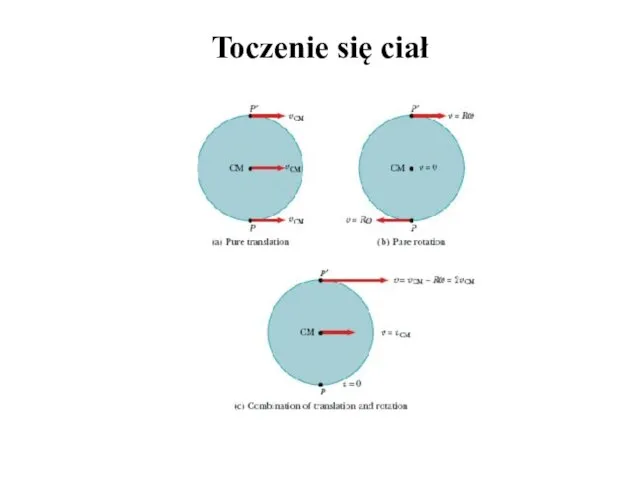
- 19. Toczenie się ciał
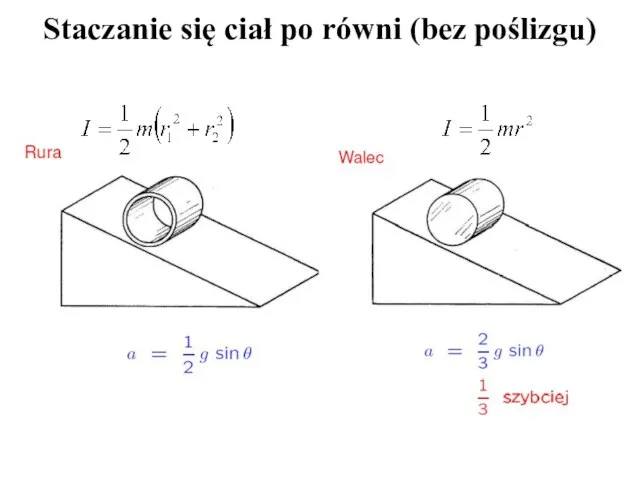
- 20. Ruch walca staczającego się po równi pochyłej bez poślizgu składa się z ruchu postępowego środka masy
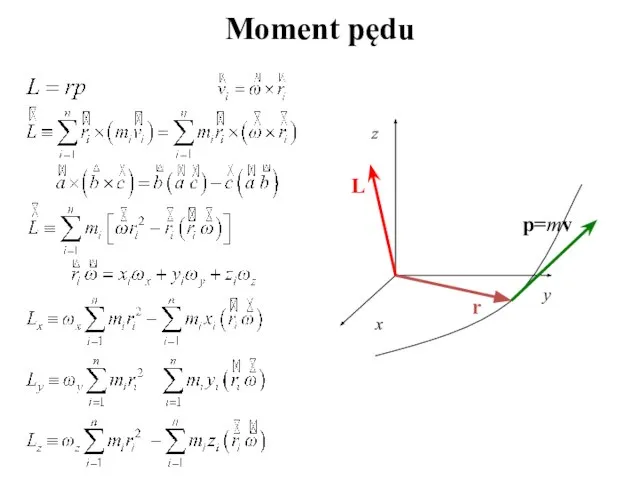
- 21. Moment pędu x z y r L p=mv
- 22. Moment pędu wprowadzając: możemy powyższy układ równań zapisać używając Tensora Bezwładności*: * wyrazy Tensora Bezwładności to
- 23. Jeżeli na bryłę A działa bryła B pewnym momentem siły MAB, to bryła B działa na
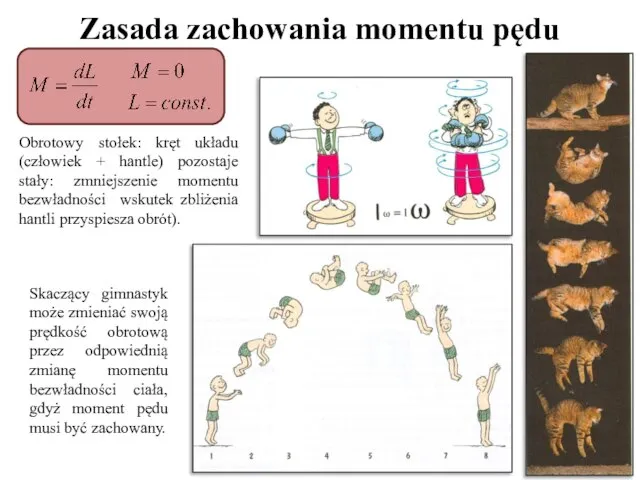
- 24. Zasada zachowania momentu pędu Obrotowy stołek: kręt układu (człowiek + hantle) pozostaje stały: zmniejszenie momentu bezwładności
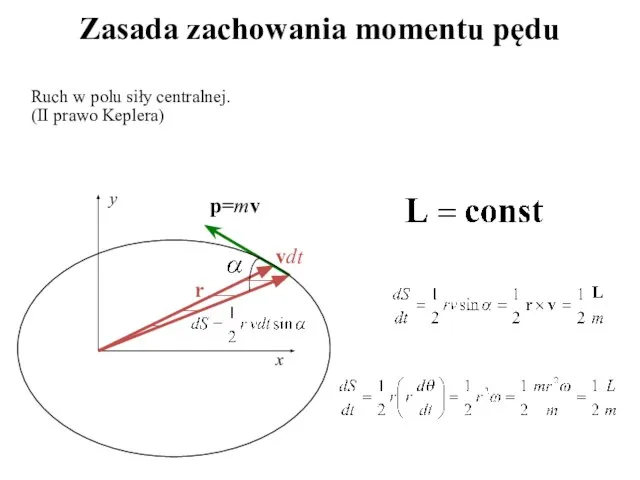
- 25. Ruch w polu siły centralnej. (II prawo Keplera) x y r p=mv vdt Zasada zachowania momentu
- 26. Analogie ruchu postępowego i obrotowego
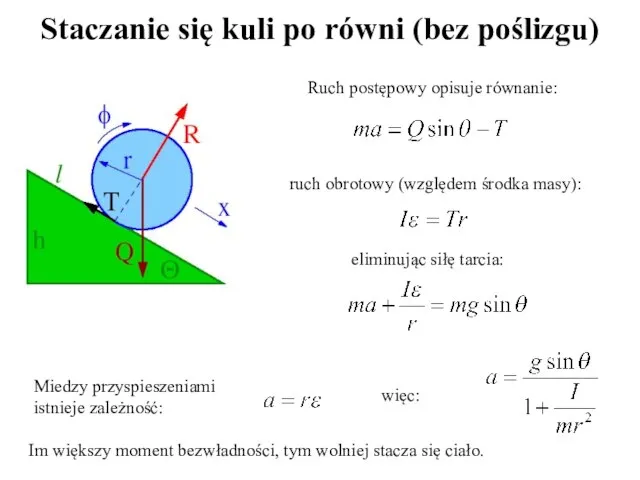
- 27. Ruch postępowy opisuje równanie: ruch obrotowy (względem środka masy): Miedzy przyspieszeniami istnieje zależność: eliminując siłę tarcia:
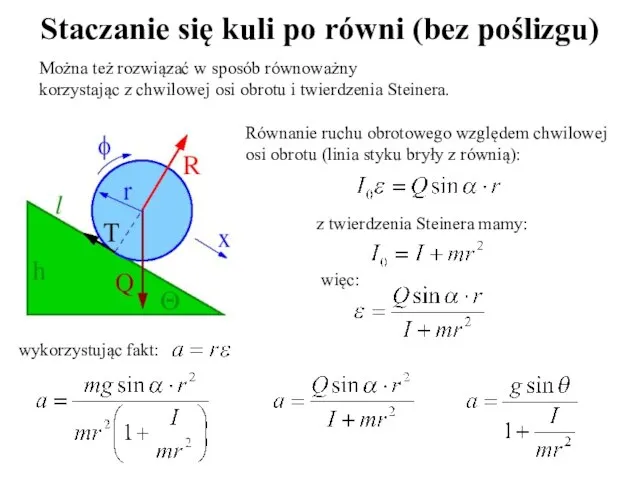
- 28. Można też rozwiązać w sposób równoważny korzystając z chwilowej osi obrotu i twierdzenia Steinera. Równanie ruchu
- 29. Staczanie się ciał po równi (bez poślizgu)
- 31. Скачать презентацию











 Электротехника и электроника. Основы теории четырехполюсников. (Лекция 13)
Электротехника и электроника. Основы теории четырехполюсников. (Лекция 13) Электромагнитное поле 9 класс Учитель физики МОУ «СОШ с. Рефлектор» Леснова Н.П.
Электромагнитное поле 9 класс Учитель физики МОУ «СОШ с. Рефлектор» Леснова Н.П. Ремонт газораспределительного механизма
Ремонт газораспределительного механизма Расчет нефтепровода на прочность и устойчивость. Практическое занятие 2
Расчет нефтепровода на прочность и устойчивость. Практическое занятие 2 Гидропривод
Гидропривод Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Презентация по физике "Вес. Невесомость" - скачать
Презентация по физике "Вес. Невесомость" - скачать  Золотое правило механики
Золотое правило механики СИЛА АРХИМЕДА И ПЛАВУЧЕСТЬ ТЕЛ
СИЛА АРХИМЕДА И ПЛАВУЧЕСТЬ ТЕЛ Қалыпты және «аномаль» дисперсия. Оны бақылау әдістері. Дисперсияның электрон теориясының негіздері. (Лекция 13)
Қалыпты және «аномаль» дисперсия. Оны бақылау әдістері. Дисперсияның электрон теориясының негіздері. (Лекция 13) Ионизирующее излучение
Ионизирующее излучение Тема урока: Распространение колебаний в упругих средах. Волны
Тема урока: Распространение колебаний в упругих средах. Волны КПД теплового двигателя
КПД теплового двигателя Расчёт кругового поворота автомобиля
Расчёт кругового поворота автомобиля Мария Кюри
Мария Кюри Микроподводные движители. Виды микро-движителей
Микроподводные движители. Виды микро-движителей Деформация и разрушение металлов. Материаловедение
Деформация и разрушение металлов. Материаловедение Конструкция беспилотного летательного аппарата
Конструкция беспилотного летательного аппарата Презентация по физике Электростатическое поле в диэлектрической среде. Поляризованность. Электрическое смещение.
Презентация по физике Электростатическое поле в диэлектрической среде. Поляризованность. Электрическое смещение.  Коливання. Електромагнітний спектр
Коливання. Електромагнітний спектр Учебный курс
Учебный курс  Что такое электродинамика
Что такое электродинамика Испытания на ударные нагрузки
Испытания на ударные нагрузки Определение разрешающей способности оптических систем. Контроль качества изображения точки
Определение разрешающей способности оптических систем. Контроль качества изображения точки Расчет установившихся режимов простейших электрических сетей. (Глава 6)
Расчет установившихся режимов простейших электрических сетей. (Глава 6) Масс-спектрометрия
Масс-спектрометрия Плазма
Плазма Оптика. Линзы
Оптика. Линзы