Содержание
- 2. Вопрос 1 Экспериментальные факты, лежащие в основе квантовой теории. Излучение абсолютно черного тела, фотоэффект и эффект
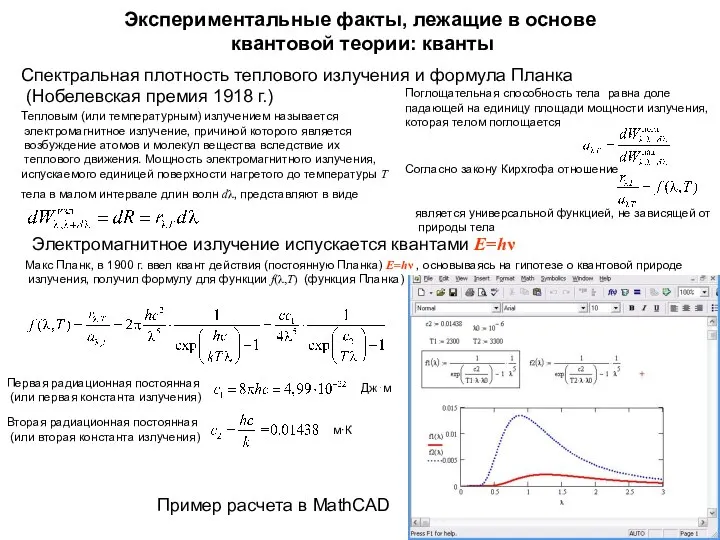
- 3. Экспериментальные факты, лежащие в основе квантовой теории: кванты Спектральная плотность теплового излучения и формула Планка (Нобелевская
- 4. Экспериментальные факты, лежащие в основе квантовой теории: фотоны Внешний фотоэффект - излучение поглощается квантами E=hν Эффект
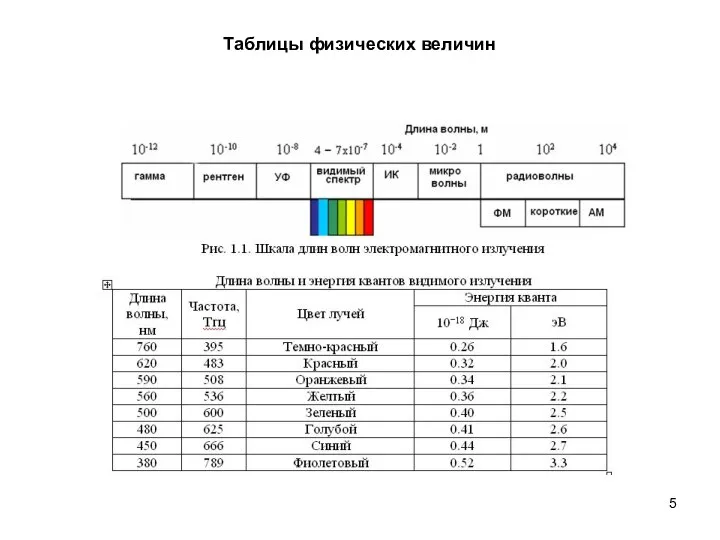
- 5. Таблицы физических величин
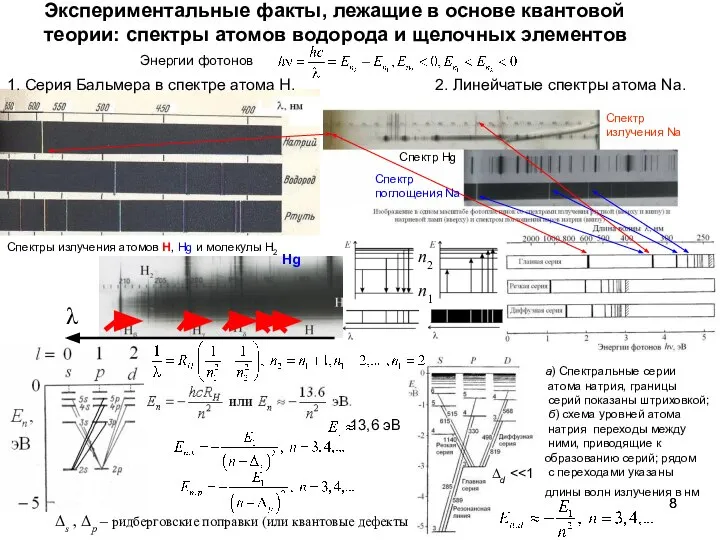
- 6. 2. Линейчатые спектры атомов Na и Hg. Спектральные серии атома натрия, границы серий показаны штриховкой; Спектр
- 7. Атом водорода по Бору Классическая картина рассеяния α-частиц с энергией Eц.м.=5 МэВ на ядрах 197Au Пример
- 8. 2. Линейчатые спектры атома Na. а) Спектральные серии атома натрия, границы серий показаны штриховкой; б) схема
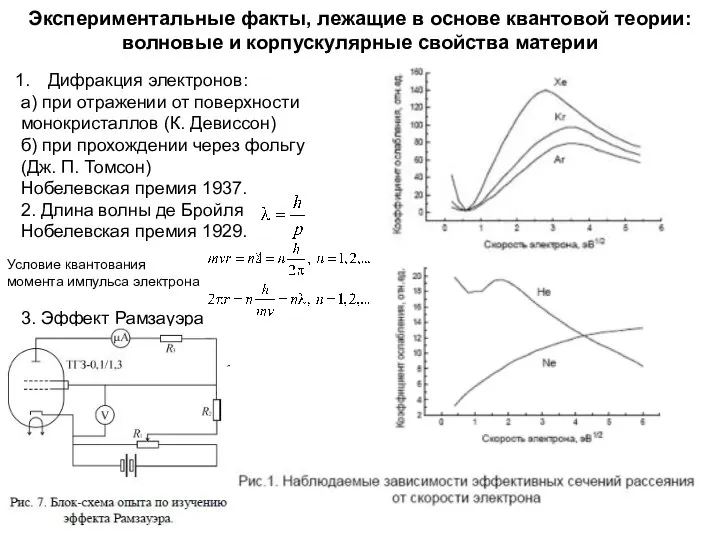
- 9. Дифракция электронов: а) при отражении от поверхности монокристаллов (К. Девиссон) б) при прохождении через фольгу (Дж.
- 10. Пример расчета длины волны де Бройля
- 11. Вопрос 2 Основные постулаты квантовой механики. Чистые и смешанные состояния квантовомеханической системы. Волновая функция, матрица плотности.
- 12. Основные постулаты квантовой механики. Физическим величинам сопоставляются операторы. Энергии сопоставлен оператор Гамильтона (гамильтониан) Н. Среднее значение
- 13. Операторы Эрмитовы (самосопряженные) операторы Комплексно сопряженный оператор для оператора Транспонированный оператор для оператора Собственные и средние
- 14. Чистые и смешанные состояния Состояния квантовой системы, описываемые волновой функцией, называются чистыми состояниями. Они соответствуют максимально
- 15. Матрица плотности Матрица плотности ρ может быть определена для состояний поляризации или других состояний для конечного
- 16. Принцип неопределенности Две физические величины не могут иметь одновременно определенные значения ни в одном состоянии, если
- 17. Вопрос 3 Описание эволюции квантовомеханических систем. Уравнения Гейзенберга и Шредингера. Стационарные состояния.
- 18. Волновая функция и уравнение Шредингера Дифференцирование операторов по времени Стационарное уравнение Шредингера Нестационарное уравнение Шредингера выражает
- 19. Изменение со временем состояний, описываемых матрицей плотности Это уравнение называют квантовым уравнением Лиувилла, так как оно
- 20. Описание эволюции квантово-механических систем. Уравнения Гейзенберга и Шредингера. Средние значения физических величин в представлениях Шредингера и
- 21. Плотность потока вероятности Уравнение непрерывности Вектор плотности тока вероятности
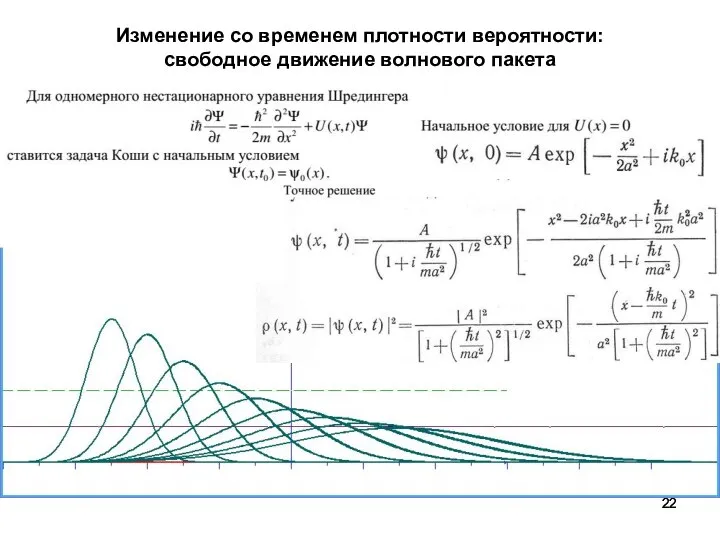
- 22. Изменение со временем плотности вероятности: свободное движение волнового пакета
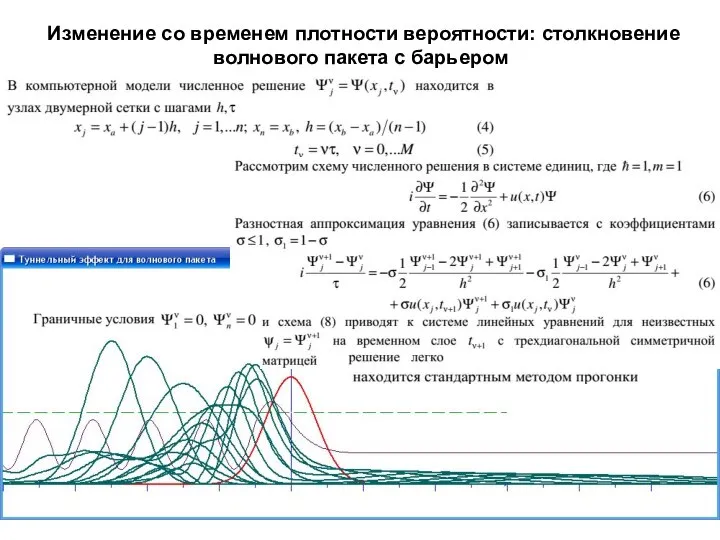
- 23. Изменение со временем плотности вероятности: столкновение волнового пакета с барьером
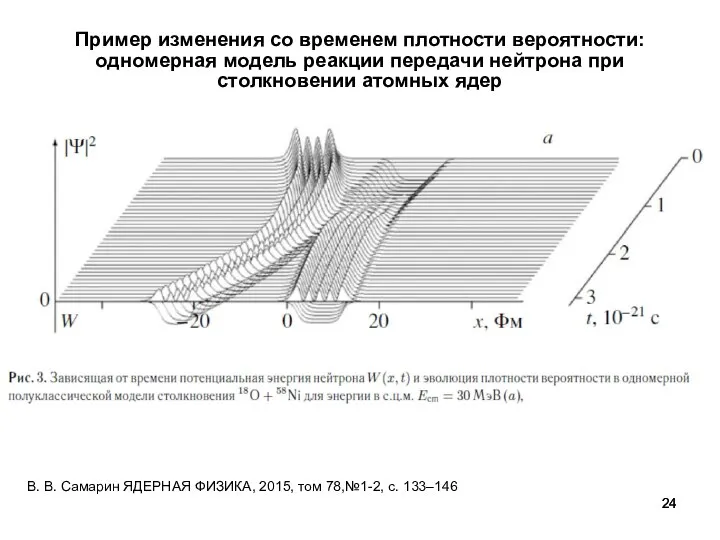
- 24. Пример изменения со временем плотности вероятности: одномерная модель реакции передачи нейтрона при столкновении атомных ядер В.
- 25. Стационарные состояния Состояния, в которых энергия имеет определенные значения (энергетические уровни), называются стационарными состояниями системы. Стационарное
- 26. Вопрос 4 Линейный квантовый гармонический осциллятор. Энергии и волновые функции стационарных состояний.
- 27. Линейный квантовый гармонический осциллятор (с помощью полиномов Эрмита Hn(x) ) Пример расчета в Maple
- 28. Линейный квантовый гармонический осциллятор (с помощью полиномов Эрмита Hn(x) ) Пример расчета в MathCAD
- 29. Линейный квантовый гармонический осциллятор (матричный метод)
- 30. Вопрос 5 Прохождение частиц через потенциальный барьер. Туннельный эффект. Квазиклассическое приближение и модель параболического барьера. Математическая
- 31. Изменение со временем плотности вероятности: столкновение волнового пакета с барьером Численное решение нестационарного уравнения Шредингера Численное
- 32. Постановка задачи о прохождения частиц через потенциальный барьер U(x) E |ψ(x)|2 Отражение Прохождение
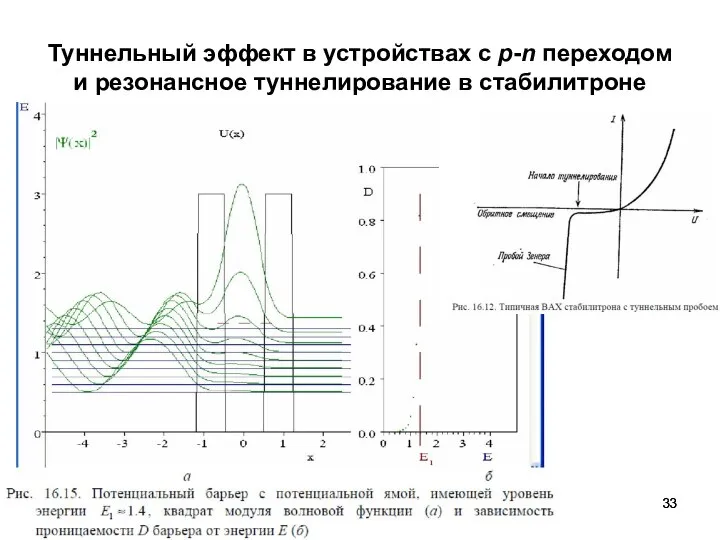
- 33. Туннельный эффект в устройствах с p-n переходом и резонансное туннелирование в стабилитроне
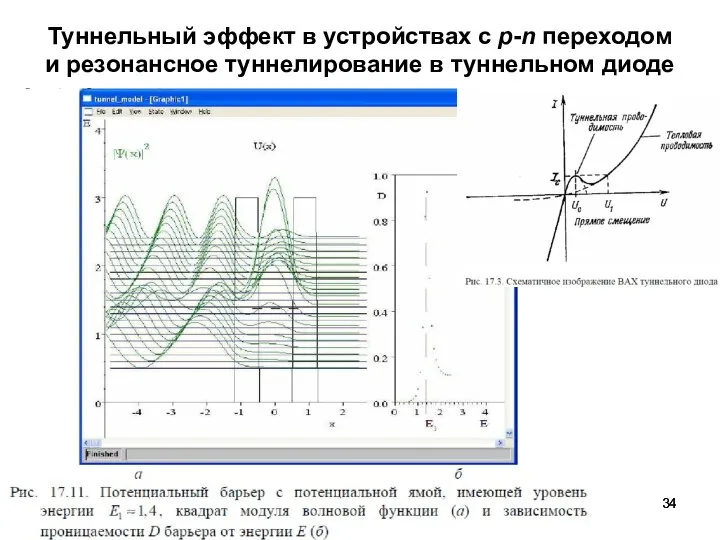
- 34. Туннельный эффект в устройствах с p-n переходом и резонансное туннелирование в туннельном диоде
- 35. Туннельный эффект при альфа-распаде
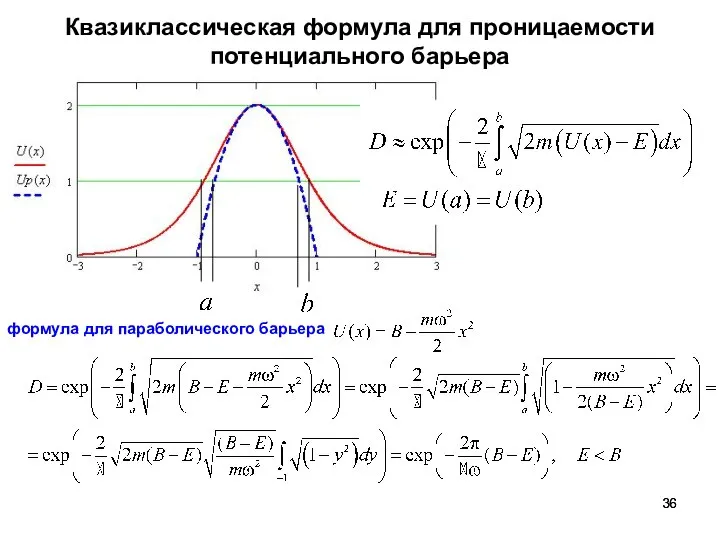
- 36. Квазиклассическая формула для проницаемости потенциального барьера формула для параболического барьера
- 37. Квазиклассическая формула для проницаемости потенциального барьера Точки поворота для потенциального барьера Точная формула Квазиклассическое приближение Условие
- 38. Пример сравнения точной и приближенных формул для проницаемости барьера Квазиклассическое приближение для параболического барьера Приближение Хилла-Уилера
- 39. Прохождение частиц через потенциальный барьер. Точное решение уравнения Шредингера для модифицированного потенциального барьера Пешля-Теллера https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D0%B8%D1%84%D0%B8%D1%86%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BF%D0%BE%D1%82%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB_%D0%9F%D1%91%D1%88%D0%BB%D1%8F_%E2%80%94_%D0%A2%D0%B5%D0%BB%D0%BB%D0%B5%D1%80%D0%B0
- 40. Вывод приближенной формулы для проницаемости параболического барьера Точная формула
- 41. Прохождение частиц через потенциальный барьер. Приближенная формула для параболического барьера с учетом центробежного потенциала − формула
- 42. Численное решение задачи о прохождение через барьер: расчеты проницаемости параболического барьера с помощью программы MathCAD и
- 43. Численное решение задачи о прохождение через барьер: расчеты проницаемости параболического барьера с помощью программы MathCAD и
- 44. Вопрос 6 Движение частиц в периодическом потенциале. Электронные состояния в кристаллах. Зонные схемы.
- 45. Движение частиц в периодическом потенциале Пусть периодический потенциал U имеет периоды трансляции a, b, c вдоль
- 46. Энергия частиц в периодическом потенциале и зонные схемы
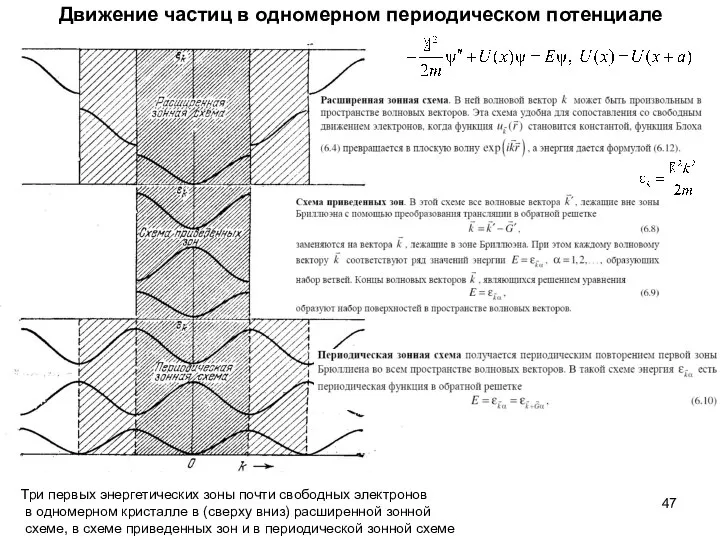
- 47. Движение частиц в одномерном периодическом потенциале Три первых энергетических зоны почти свободных электронов в одномерном кристалле
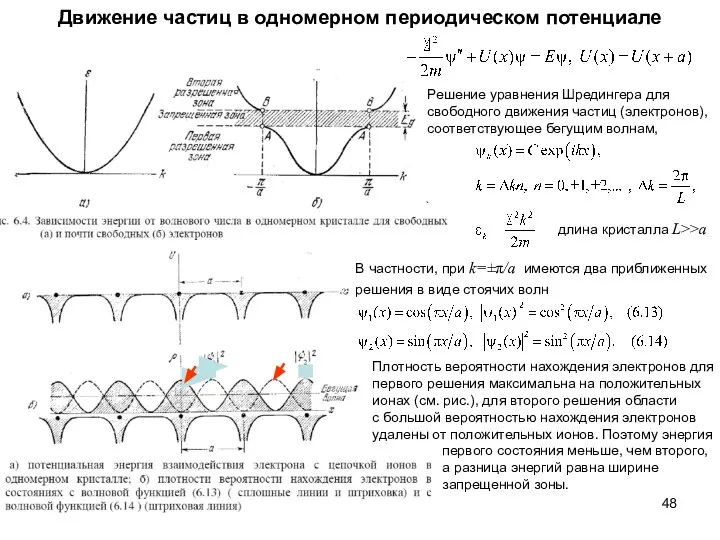
- 48. Движение частиц в одномерном периодическом потенциале длина кристалла L>>a Решение уравнения Шредингера для свободного движения частиц
- 49. Энеретические зоны в одномерном периодическом потенциале Полученные состояния заполняются электронами по принципу Паули – состояние с
- 50. Энеретические зоны в одномерном периодическом потенциале и эффективная масса Эффективная масса электрона Таким образом, влияние взаимодействия
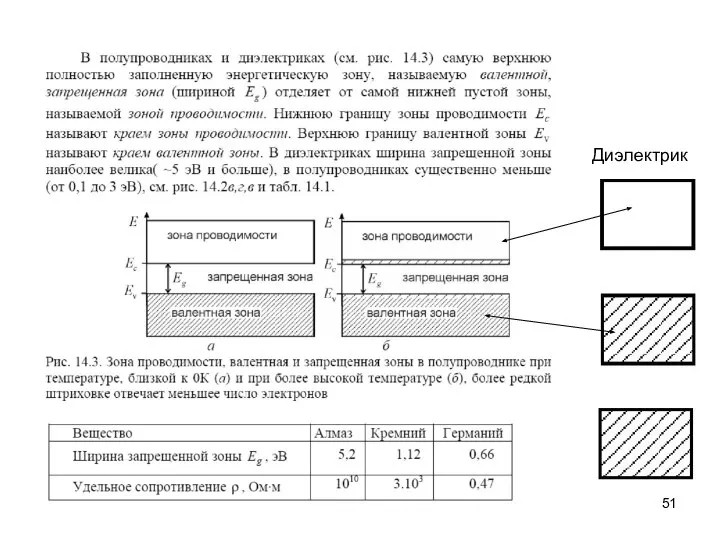
- 51. Диэлектрик
- 52. Пример точного решения уравнения Шредингера для периодического потенциала – “гребенка” Дирака
- 55. Скачать презентацию







































 Масса и сила. Взаимодействие тел. Законы динамики. Силы в природе
Масса и сила. Взаимодействие тел. Законы динамики. Силы в природе Закон всемирного тяготения Ньютона
Закон всемирного тяготения Ньютона Презентация по физике "Спектры и излучения" - скачать бесплатно
Презентация по физике "Спектры и излучения" - скачать бесплатно Физические принципы, основные виды и клиническое значение ЭХОкг
Физические принципы, основные виды и клиническое значение ЭХОкг Звуки в воде Звуки, которые мы не слышим.
Звуки в воде Звуки, которые мы не слышим. Презентация по физике "Фізика754" - скачать
Презентация по физике "Фізика754" - скачать  Потенциальная и кинетическая энергия
Потенциальная и кинетическая энергия Магнитное поле. Учитель: Галина Николаевна Студенка группы 1414 Моисеенкова Мария Академия индустрии красоты «Локон».
Магнитное поле. Учитель: Галина Николаевна Студенка группы 1414 Моисеенкова Мария Академия индустрии красоты «Локон». Э.М. Спиридонов. Эволюция минералов кадмия в зоне гипергенеза
Э.М. Спиридонов. Эволюция минералов кадмия в зоне гипергенеза Отношение сигнал-шум на выходе приёмника ЧМ сигнала
Отношение сигнал-шум на выходе приёмника ЧМ сигнала Гармонические колебания
Гармонические колебания Презентация по физике "Ультразвук та його використання" - скачать бесплатно
Презентация по физике "Ультразвук та його використання" - скачать бесплатно Столкновения при наличии трения. Тема 1
Столкновения при наличии трения. Тема 1 Детали генератора переменного тока
Детали генератора переменного тока Презентация по физике "Дисперсия и ее свойства" - скачать бесплатно
Презентация по физике "Дисперсия и ее свойства" - скачать бесплатно Динаамика. Вращательное движение. Энергия. (Лекция 3)
Динаамика. Вращательное движение. Энергия. (Лекция 3) Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения Деформація тіл. Види деформації
Деформація тіл. Види деформації Полупроводниковые оптические усилители. Нелинейные оптические усилители
Полупроводниковые оптические усилители. Нелинейные оптические усилители Элементы механики жидкостей
Элементы механики жидкостей Зубчатые колеса
Зубчатые колеса Подготовил ученик 8 «А» класса МОУ СОШ № 7 г.о.Новокуйбышевска Самарская область Шлыков Влад. «Исследование электромагнитного из
Подготовил ученик 8 «А» класса МОУ СОШ № 7 г.о.Новокуйбышевска Самарская область Шлыков Влад. «Исследование электромагнитного из Звуковые волны. Скорость звука. (10 класс)
Звуковые волны. Скорость звука. (10 класс) Экспериментальные методы исследования частиц
Экспериментальные методы исследования частиц  Тема 2.5. Сорбционные гигрометры
Тема 2.5. Сорбционные гигрометры Молекулярно-кинетическая теория
Молекулярно-кинетическая теория Строение формаций. Форма залежей. (Лекция 3)
Строение формаций. Форма залежей. (Лекция 3) Грозова енергетика
Грозова енергетика