Содержание
- 2. Найдем математическое ожидание и дисперсию этой случайной величины. Например, пусть случайная величина Х задана рядом распределения:
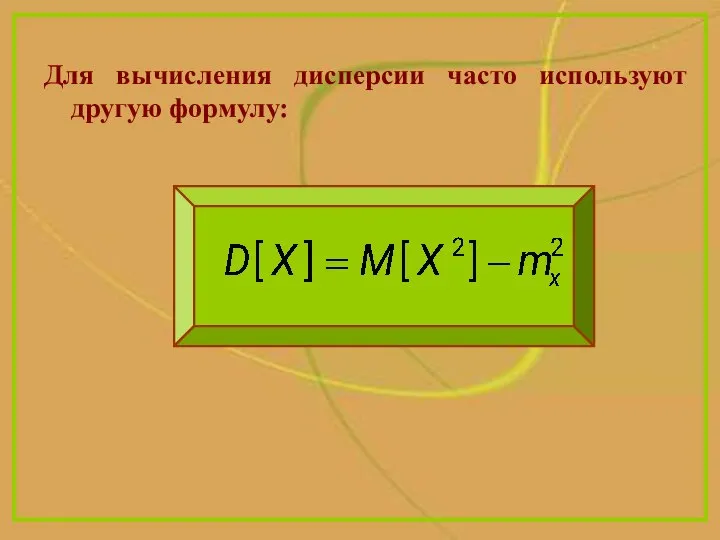
- 3. Для вычисления дисперсии часто используют другую формулу:
- 4. Доказательство: Используем свойства математического ожидания:
- 5. СВОЙСТВА ДИСПЕРСИИ Дисперсия от постоянной величины равна нулю: D[C]=0, C=const 1
- 6. Доказательство: Используем второе выражение для дисперсии. Так как M[C]=C, M[C2]=C2 то D[C]=M[C2]-(M[C])2=C2-C2=0
- 7. Дисперсия суммы случайной величины Х и постоянной величины С равна дисперсии величины Х : D[X+С]=D[X] 2
- 8. Доказательство: По свойству математического ожидания: М[X+С]=M[X]+С Поэтому на основании определения дисперсии:
- 9. Постоянная величина выносится за знак дисперсии в квадрате: D[k X]=k2 D[X] 3
- 10. Доказательство: По свойству математического ожидания: Используем определение дисперсии:
- 11. 4 Дисперсия всегда неотрицательна:
- 12. 5 Дисперсия суммы двух случайных величин находится по формуле:
- 13. Величина KXY называется корреляционным моментом случайных величин X и Y:
- 14. Математическое ожидание суммы равно сумме математических ожиданий: Распишем дисперсию суммы случайных величин по определению дисперсии: Доказательство:
- 15. Перегруппируем слагаемые: Снова используем свойства математического ожидания: Под знаком математического ожидания раскрываем квадрат суммы:
- 17. Скачать презентацию


![СВОЙСТВА ДИСПЕРСИИ Дисперсия от постоянной величины равна нулю: D[C]=0, C=const 1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1267073/slide-4.jpg)
![Доказательство: Используем второе выражение для дисперсии. Так как M[C]=C, M[C2]=C2 то D[C]=M[C2]-(M[C])2=C2-C2=0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1267073/slide-5.jpg)
![Дисперсия суммы случайной величины Х и постоянной величины С равна дисперсии величины Х : D[X+С]=D[X] 2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1267073/slide-6.jpg)
![Доказательство: По свойству математического ожидания: М[X+С]=M[X]+С Поэтому на основании определения дисперсии:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1267073/slide-7.jpg)
![Постоянная величина выносится за знак дисперсии в квадрате: D[k X]=k2 D[X] 3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1267073/slide-8.jpg)






 Анализ текстуры. Прямые полюсные фигуры
Анализ текстуры. Прямые полюсные фигуры Строение и физические свойства вещества
Строение и физические свойства вещества Краткая история развития радиосвязи
Краткая история развития радиосвязи Балаклеївська спеціалізована школа І-ІІІ ступенів №1 імені Євгенії Гуглі Розвиток фізики як науки
Балаклеївська спеціалізована школа І-ІІІ ступенів №1 імені Євгенії Гуглі Розвиток фізики як науки  Исследование деления шага шагового двигателя для высокоточного перемещения объектов
Исследование деления шага шагового двигателя для высокоточного перемещения объектов Дифракция света. (Лабораторная работа)
Дифракция света. (Лабораторная работа) Магнітне поле. Магнітний потік
Магнітне поле. Магнітний потік Физика. Проект. Шаблон
Физика. Проект. Шаблон Агрегатные состояния вещества
Агрегатные состояния вещества Презентация по физике "Давление в жидкостях и газе" - скачать бесплатно
Презентация по физике "Давление в жидкостях и газе" - скачать бесплатно Волны. Звук
Волны. Звук Строение атома. Лекция 3
Строение атома. Лекция 3 Ожэ-электронная спектроскопия
Ожэ-электронная спектроскопия Механическое движение
Механическое движение Правило буравчика, правило правой руки
Правило буравчика, правило правой руки Презентация по Физике на тему Электрический ток в различных средах Работа ученика 10 класса «Г» Коровкина Владислава
Презентация по Физике на тему Электрический ток в различных средах Работа ученика 10 класса «Г» Коровкина Владислава Лабораторные работы по физике 8 класс
Лабораторные работы по физике 8 класс Магнитные подшипники
Магнитные подшипники Презентация по физике Электроемкость
Презентация по физике Электроемкость 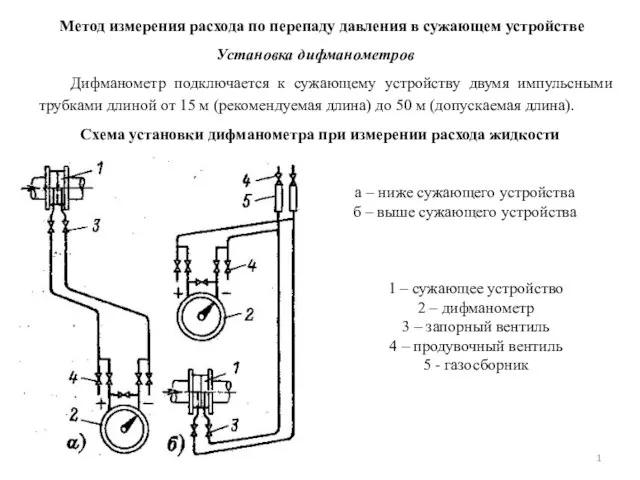 Метод измерения расхода по перепаду давления в сужающем устройстве. Установка дифманометров
Метод измерения расхода по перепаду давления в сужающем устройстве. Установка дифманометров Закон Кирхгофа
Закон Кирхгофа Ультразвуковой контроль
Ультразвуковой контроль Показатели качества регулирования. Точность регулирования
Показатели качества регулирования. Точность регулирования Свободное падение
Свободное падение Презентация по физике Физика твердого тела часть 3
Презентация по физике Физика твердого тела часть 3 Соударение твердых тел
Соударение твердых тел Кинематика твёрдого тела
Кинематика твёрдого тела Физика колебаний
Физика колебаний