Содержание
- 2. Цели проекта: Исследовать возможность применения знаний элементов линейной алгебры на занятиях электротехники Создать электронное учебное пособие,
- 3. Структура электронного учебного пособия Пособие состоит из трех частей: Элементы линейной алгебры (теоретический материал) Электротехника (Расчет
- 4. Элементы линейной алгебры в электротехнике Выполнил: Вараксин Р.А. гр.203 Преподаватели: Никитина Н.В., Касаткина И.С.
- 5. Содержание Элементы линейной алгебры Электротехника Электротехническая задача Решение систем линейных уравнений методом Гаусса в Excel
- 6. Содержание Определение матрицы Виды матриц Действия над матрицами Системы линейных уравнений и их решения Решение систем
- 7. Определение матрицы Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов.
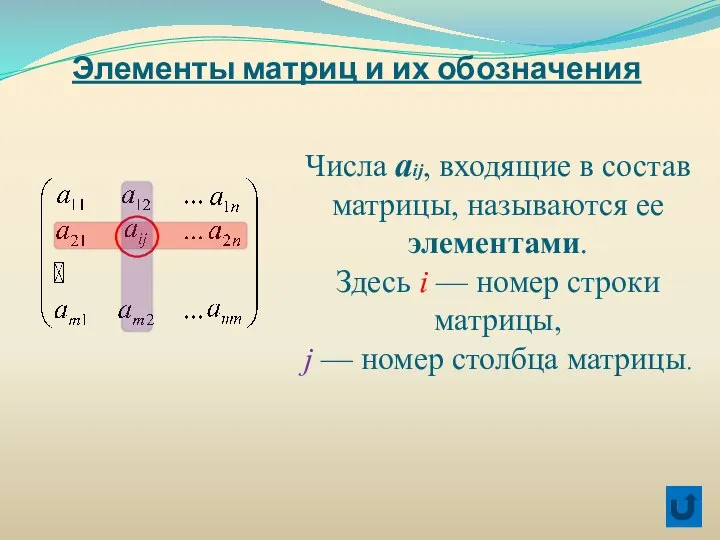
- 8. Элементы матриц и их обозначения Числа aij, входящие в состав матрицы, называются ее элементами. Здесь i
- 9. Виды матриц Прямоугольная Квадратная (m ≠n) (m=n) Для квадратной матрицы определено понятие диагоналей Частные случаи Частные
- 10. Прямоугольная матрица Если в матрице типа m×n, m=1,то матрица называется матрица-строка Если в матрице типа m×n,
- 11. Квадратная матрица Диагональная Скалярная Единичная Треугольная: нижняя, верхняя
- 12. Диагонали матриц Диагональ, содержащую элементы а11,а22,…, аmn, будем называть главной, а диагональ ,содержащую элементы a1n,a22,…,am1 –
- 13. Диагональная матрица Матрица называется диагональной, если все элементы матрицы, кроме элементов главной диагонали равны 0 Например:
- 14. Скалярная матрица Если все элементы главной диагонали диагональной матрицы равны между собой, то матрица называется скалярной
- 15. Единичная матрица Диагональная матрица, все элементы главной диагонали которой равны 1, называется единичной матрицей
- 16. Треугольная матрица Квадратная матрица, у которой все элементы, лежащие выше (или ниже) главной диагонали равны 0,
- 17. Действия над матрицами Сложение Умножение матрицы на число Транспонирование Умножение матриц
- 18. Сложение матриц Определение: Суммой двух матриц А и В называется матрица С, элементы которой равны сумме
- 19. Свойства сложения матриц Переместительный закон сложения: А+В = В+А, где А и В – либо квадратные
- 20. Умножение матрицы на число Определение: Произведением матрицы А на число k называется матрица С, каждый элемент
- 21. Транспонирование матрицы Определение: Транспонированная матрица - это матрица, полученная из исходной путем замены строк на столбцы.
- 22. Умножение матриц Что бы получить элемент, стоящий на пересечении строки и столбца матрицы-произведения, нужно все элементы
- 23. Свойства умножения матриц Произведение не подчиняется переместительному закону: А·В ≠ В·А Сочетательный закон умножения: (А·В)·С=А·(В·С) Распределительный
- 24. Системы линейных уравнений
- 25. Решение уравнений методом Гаусса
- 26. «Математика – царица всех наук» Карл Фридрих Гаусс (1777-1855 г.г.) – немецкий математик, физик, астроном, геодезист.
- 27. В чем его суть? Он состоит в следующем: систему уравнений приводят к эквивалентной ей системе с
- 28. Прямой ход При выполнении прямого хода используют следующие преобразования: Умножение и деление коэффициентов свободных членов на
- 29. Содержание Электрическая схема (справочный материал) Расчет цепи постоянного тока Алгоритм расчета цепей методом уравнений Кирхгофа Первый
- 30. Расчет цепей постоянного тока сводится к нахождению токов, протекающих по ветвям цепи путем составления системы уравнений
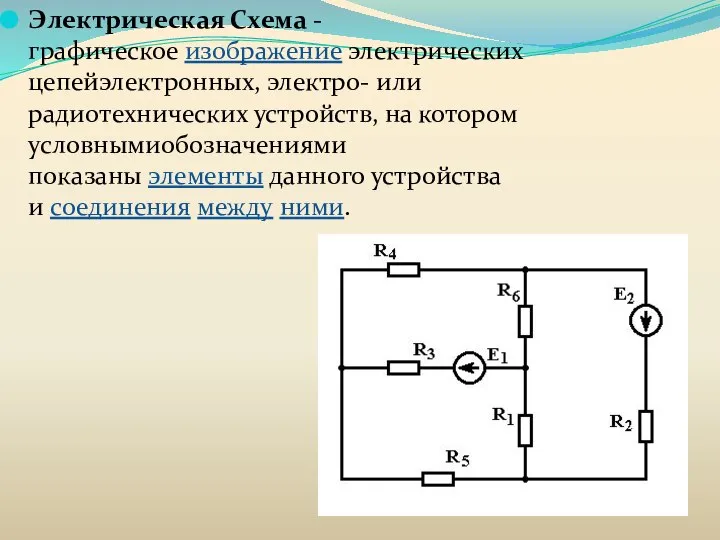
- 31. Электрическая Схема - графическое изображение электрических цепейэлектронных, электро- или радиотехнических устройств, на котором условнымиобозначениями показаны элементы
- 32. Узел- место соединения трех и более ветвей А B C D
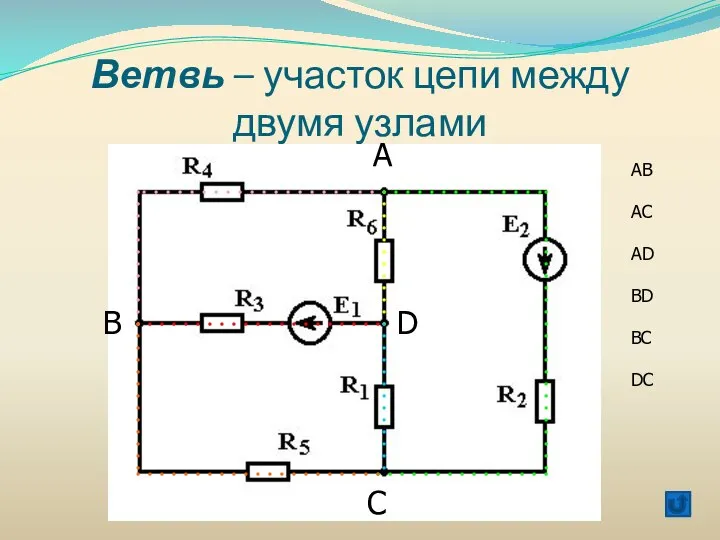
- 33. Ветвь – участок цепи между двумя узлами А B C D АВ АС АD BD BC
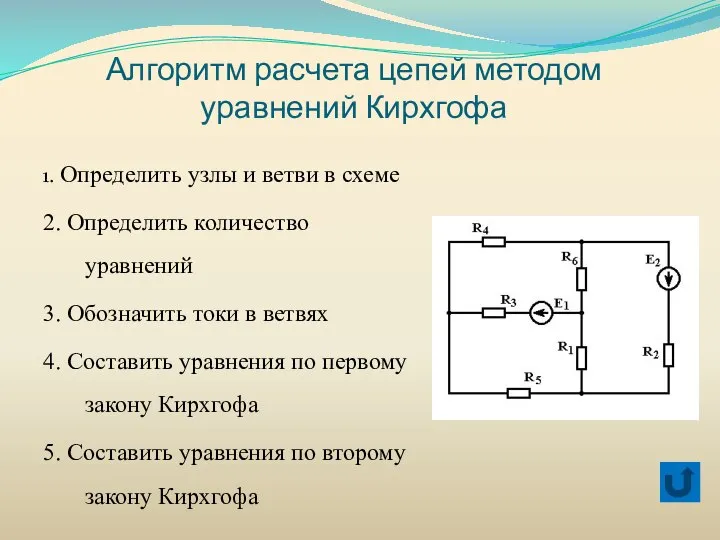
- 34. Алгоритм расчета цепей методом уравнений Кирхгофа 1. Определить узлы и ветви в схеме 2. Определить количество
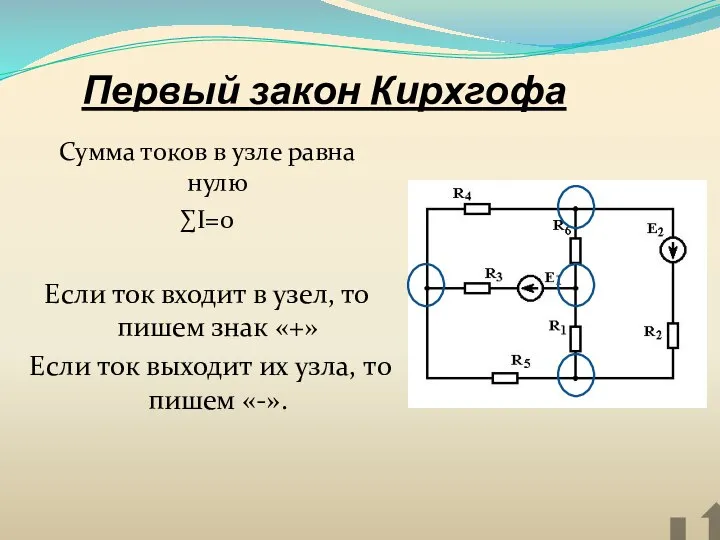
- 35. Первый закон Кирхгофа Сумма токов в узле равна нулю ∑I=0 Если ток входит в узел, то
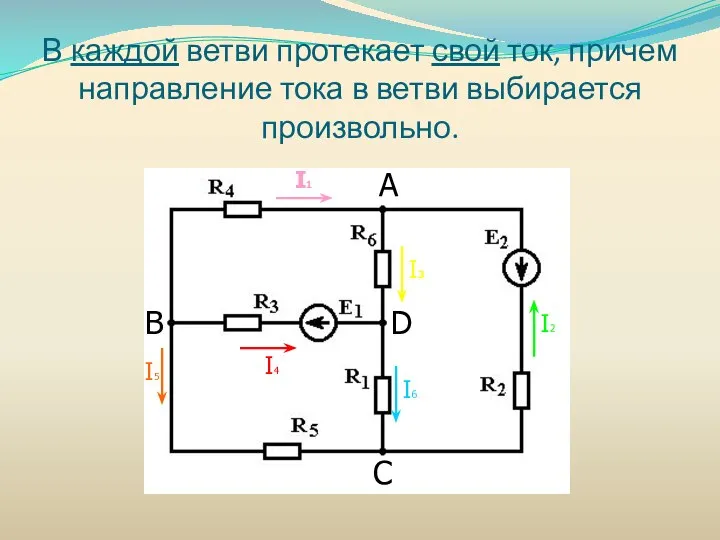
- 36. В каждой ветви протекает свой ток, причем направление тока в ветви выбирается произвольно. А B C
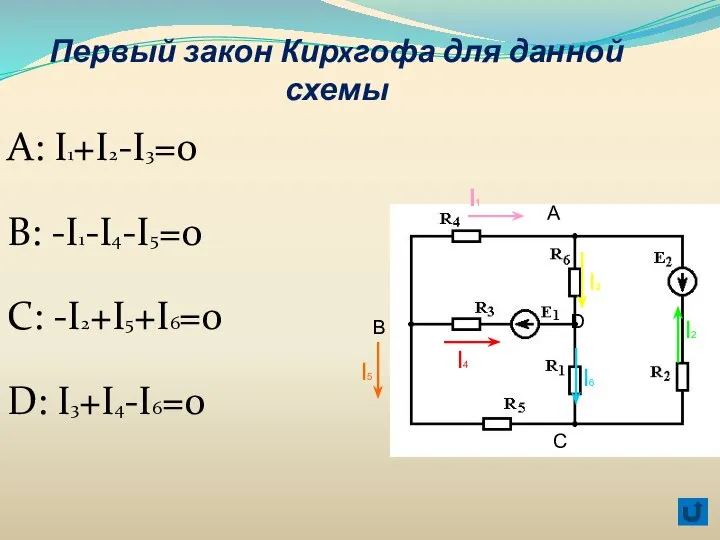
- 37. Первый закон Кирxгофа для данной схемы А: I1+I2-I3=0 B: -I1-I4-I5=0 C: -I2+I5+I6=0 D: I3+I4-I6=0 А B
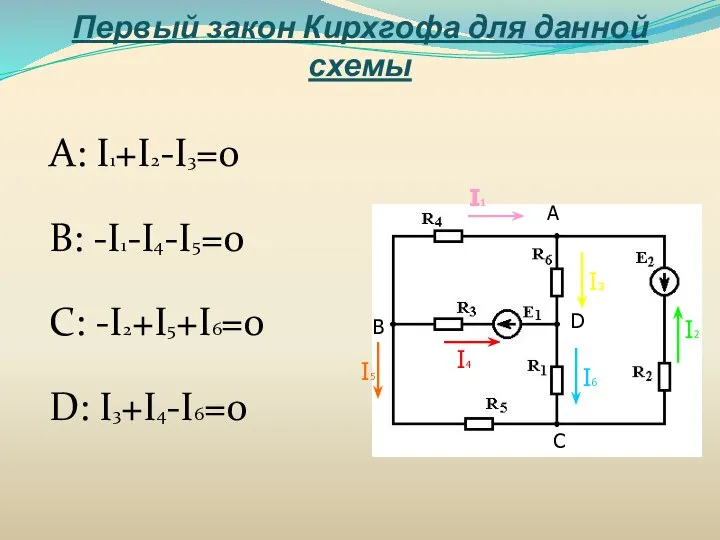
- 38. Первый закон Кирхгофа для данной схемы А: I1+I2-I3=0 B: -I1-I4-I5=0 C: -I2+I5+I6=0 D: I3+I4-I6=0 А B
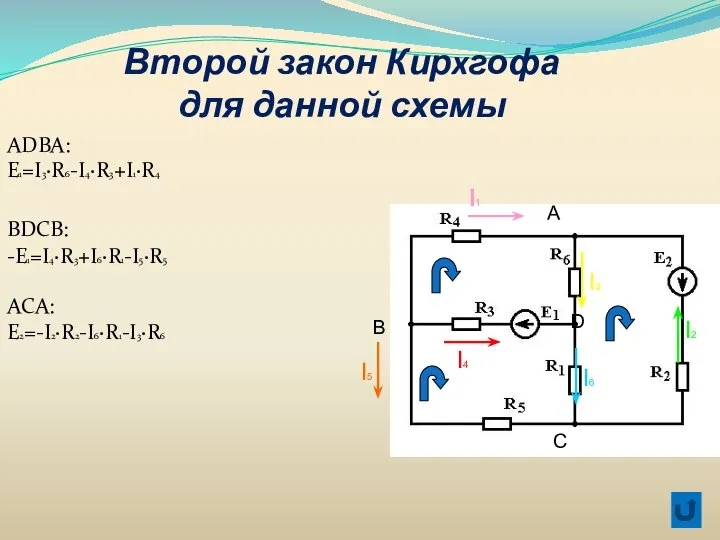
- 39. Второй закон Кирхгофа Алгебраическая сумма ЭДС в замкнутом контуре равна алгебраической сумме падений напряжения этого контура.
- 40. Второй закон Кирxгофа для данной схемы ADBA: E1=I3·R6-I4·R3+I1·R4 BDCB: -E1=I4·R3+I6·R1-I5·R5 ACA: E2=-I2·R2-I6·R1-I3·R6 А B C D
- 41. Количество уравнений Общее количество уравнений равно числу ветвей. Из них количество уравнений по первому закону составляет
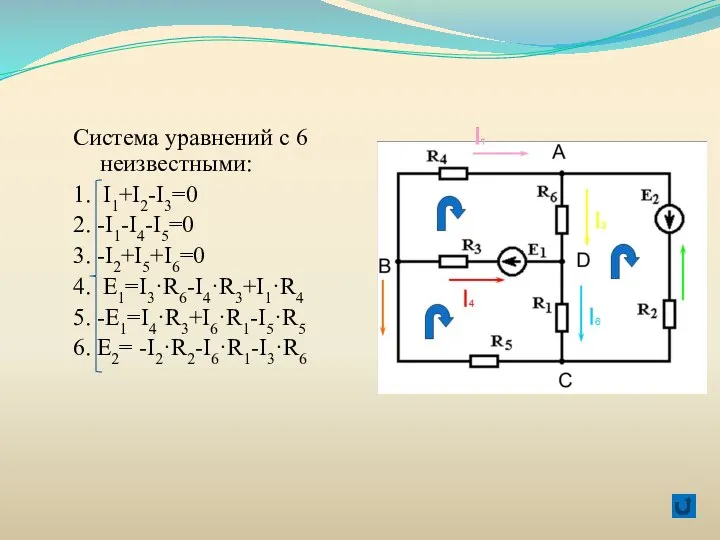
- 42. Система уравнений с 6 неизвестными: 1. I1+I2-I3=0 2. -I1-I4-I5=0 3. -I2+I5+I6=0 4. E1=I3·R6-I4·R3+I1·R4 5. -E1=I4·R3+I6·R1-I5·R5 6.
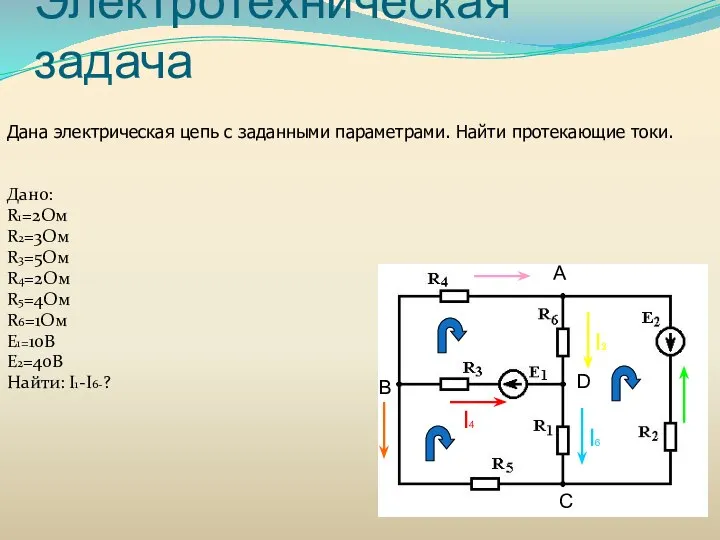
- 43. Электротехническая задача Дано: R1=2Ом R2=3Ом R3=5Ом R4=2Ом R5=4Ом R6=1Ом E1=10B E2=40B Найти: I1-I6-? А B C
- 44. 1. Составим расширенную матрицу по условию задачи 2. От 2 и 4 строк отнимаем 1 строку,
- 45. 5. от 2, 4 и 6 строк отнимаем 3 строку, умноженную соответственно на -1; 1; -4
- 46. 9. от 1, 2, 3, 4 и 6 строк отнимаем 5 строку, умноженную соответственно на 0,75;
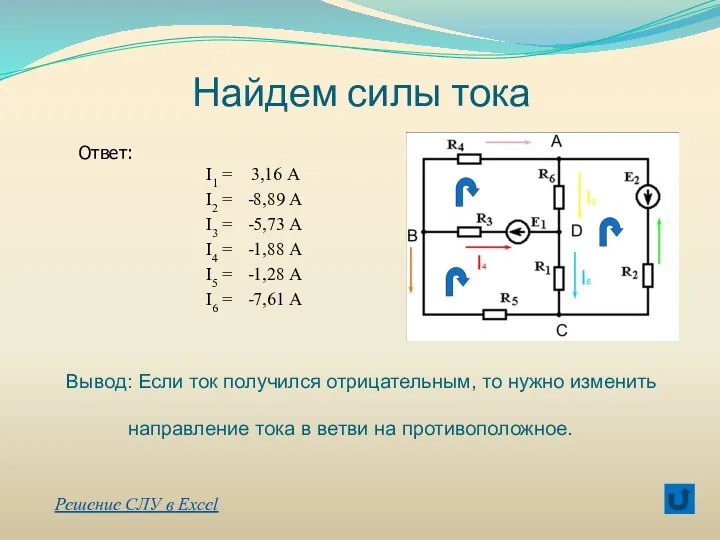
- 47. Найдем силы тока Вывод: Если ток получился отрицательным, то нужно изменить направление тока в ветви на
- 49. Скачать презентацию


































 Закон всемирного тяготения. Искусственные спутники Земли. Решение задач
Закон всемирного тяготения. Искусственные спутники Земли. Решение задач Плоская система сил
Плоская система сил Гамма – излучение
Гамма – излучение Скорость прямолинейного равноускоренного движения. График скорости
Скорость прямолинейного равноускоренного движения. График скорости Устройство подвески Лада Веста
Устройство подвески Лада Веста Пространственная система сил
Пространственная система сил Эллиптическое движение
Эллиптическое движение Радиоактивные батарейки
Радиоактивные батарейки Что изучает физика
Что изучает физика Магнитное поле. Его свойства
Магнитное поле. Его свойства Смачивание и капиллярность в природе и технике
Смачивание и капиллярность в природе и технике Лазер и его применение
Лазер и его применение Основы кинематики
Основы кинематики Ядерный магнитный резонанс
Ядерный магнитный резонанс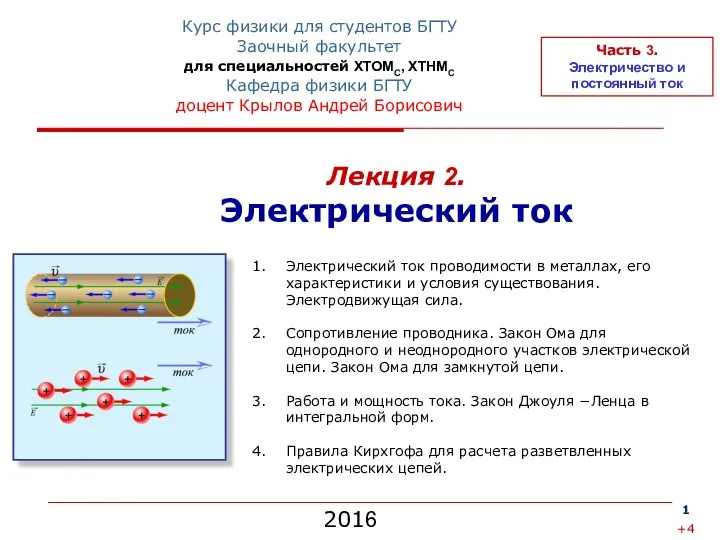 Электрический ток. (лекция 2)
Электрический ток. (лекция 2) Теория переноса ионизирующего излучения
Теория переноса ионизирующего излучения Телескопы: линзовые, зеркальные, зеркально-линзовые
Телескопы: линзовые, зеркальные, зеркально-линзовые Методика подготовки к ЕГЭ, специфика преподавания физики. Примеры
Методика подготовки к ЕГЭ, специфика преподавания физики. Примеры Магнитное поле. Магниты естественные и искусственные
Магнитное поле. Магниты естественные и искусственные Агрегатное состояние вещества Приготовила:Верхозина Анастасия
Агрегатное состояние вещества Приготовила:Верхозина Анастасия  Аттестационная работа. Методическая разработка по выполнению проекта Невидимые оковы тяжести. Земное притяжение
Аттестационная работа. Методическая разработка по выполнению проекта Невидимые оковы тяжести. Земное притяжение Термодинамика – табиғатта жүретін жылулық қозғалыс туралы ғылым
Термодинамика – табиғатта жүретін жылулық қозғалыс туралы ғылым Схемы многокорпусных выпарных установок
Схемы многокорпусных выпарных установок Замена маслосъёмных колпачков автомобиля ВАЗ2110
Замена маслосъёмных колпачков автомобиля ВАЗ2110 Закон сохранения энергии
Закон сохранения энергии Термомеханические испытания. Методы и средства механических испытаний
Термомеханические испытания. Методы и средства механических испытаний Модельный ряд двигателей ЗМЗ
Модельный ряд двигателей ЗМЗ Биофизика дыхания. Объемы и емкости легких
Биофизика дыхания. Объемы и емкости легких