Содержание
- 2. Тема 6. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ План лекции 1. Энергия системы точечных зарядов. 2. Энергия заряженных проводников
- 3. 1. Энергия системы точечных зарядов Рассмотрим два неподвижных точечных заряда q1 и q2, расположенные на некотором
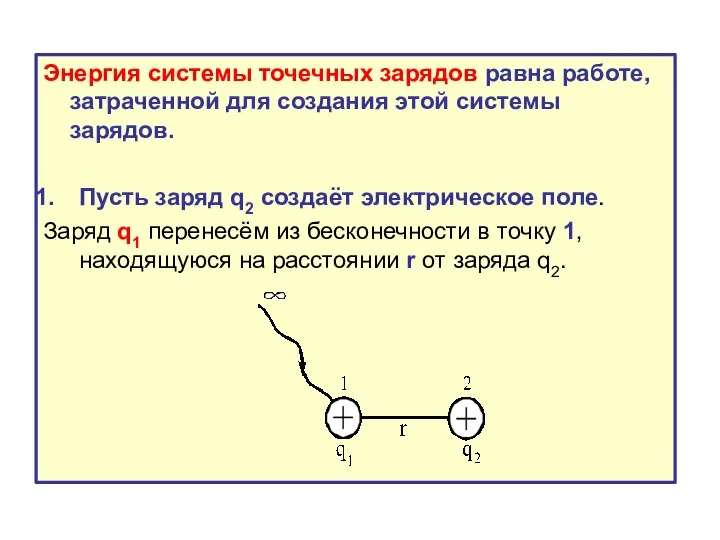
- 4. Энергия системы точечных зарядов равна работе, затраченной для создания этой системы зарядов. Пусть заряд q2 создаёт
- 5. Работа по переносу q1 равна Поскольку ϕ ∞ = 0, то Знак минус указывает на то,
- 6. 2. Пусть заряд q1 создает поле. Заряд q2 перенесем из бесконечности в точку 2, расположенную на
- 7. В обоих случаях формулы для вычисления работы получились одинаковыми, независимо от условий создания системы двух зарядов:
- 8. Потенциальная энергия взаимодействия двух точечных зарядов, расположенных на расстоянии r: Эту формулу можно записать по-другому, взяв
- 9. Последнюю формулу можно обобщить для системы многих зарядов, записав ее в виде: В формуле: i –
- 10. 2. Энергия заряженного проводника и конденсатора Собственная энергия заряженного проводника Заряд, находящийся на заряженном проводнике, можно
- 11. Будем заряжать проводник, перенося заряды малыми порциями dq с нулевого уровня потенциала на поверхность проводника. Пусть
- 12. Полная работа А вычисляется как В интегральное выражение подставим потенциал, выраженный через электроёмкость: Тогда работа А
- 13. Делая соответствующие замены и , получим для потенциальной энергии заряженного проводника дополнительные выражения: Собственная энергия конденсатора
- 14. Элементарная работа, совершаемая силами поля при переносе заряда dq равна: Перейдём к вычислению потенциальной энергии: Тогда
- 15. Учитывая, что в конце зарядки полный заряд , получим или Обозначим разность потенциалов как напряжение Δϕ
- 16. 3. Энергия электростатического поля Преобразуем, выражение для энергии конденсатора так, чтобы в него вошли характеристики поля
- 17. Произведём замены: и Для энергии электрического поля в конденсаторе получим выражение: Введём понятие объёмной плотности энергии
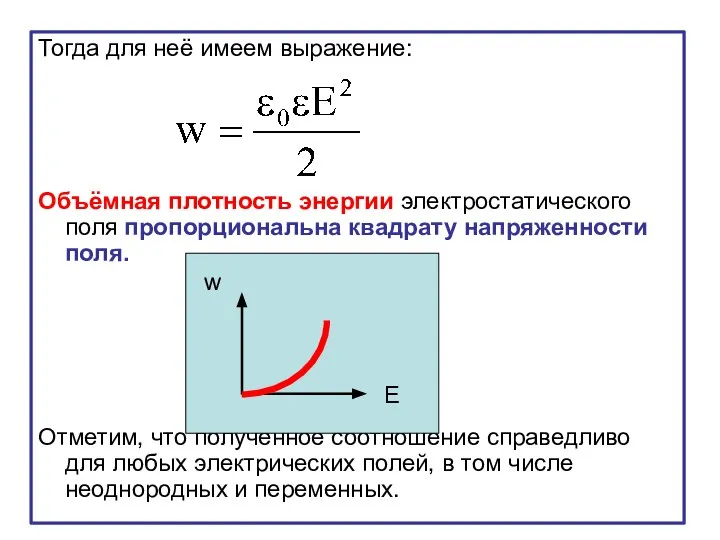
- 18. Тогда для неё имеем выражение: Объёмная плотность энергии электростатического поля пропорциональна квадрату напряженности поля. Отметим, что
- 20. Скачать презентацию















 Электрический ток. Источники электрического тока
Электрический ток. Источники электрического тока Физикалық шамаларды өлшеу бірліктері
Физикалық шамаларды өлшеу бірліктері ПРЕЗЕНТАЦИЯ по физике на тему «Виды излучений»
ПРЕЗЕНТАЦИЯ по физике на тему «Виды излучений»  Механическая энергия Закон сохранения энергии
Механическая энергия Закон сохранения энергии Аэрокосмическая школа. Разработка технологии производства активных элементов миниатюрных вакуумных полупроводниковых приборов
Аэрокосмическая школа. Разработка технологии производства активных элементов миниатюрных вакуумных полупроводниковых приборов Биполярные транзисторы
Биполярные транзисторы Гидродинамика. Полная диаграмма циркуляции воды в трубе
Гидродинамика. Полная диаграмма циркуляции воды в трубе Структурная схема механизма
Структурная схема механизма Ядерный магнитный резонанс
Ядерный магнитный резонанс Әлем онтологиясының физикалық негіздерін зерттеу
Әлем онтологиясының физикалық негіздерін зерттеу Двигатель внутреннего сгорания. Паровая турбина
Двигатель внутреннего сгорания. Паровая турбина Аттестационная работа. Тематическое планирование элективного курса «Физические законы вокруг нас»
Аттестационная работа. Тематическое планирование элективного курса «Физические законы вокруг нас» Познавательная сейсмология. Научно-популярные материалы
Познавательная сейсмология. Научно-популярные материалы Квантовая физика- раздел современной физики, в котором изучаются свойства, строение атомов и молекул, движение и взаимодействи
Квантовая физика- раздел современной физики, в котором изучаются свойства, строение атомов и молекул, движение и взаимодействи Влияние предварительной деформации на эффект памяти формы в интерметаллиде TiNi.
Влияние предварительной деформации на эффект памяти формы в интерметаллиде TiNi. А.М. НОВИКОВ Д.А. НОВИКОВ МЕТОДОЛОГИЯ НАУЧНОГО ИССЛЕДОВАНИЯ
А.М. НОВИКОВ Д.А. НОВИКОВ МЕТОДОЛОГИЯ НАУЧНОГО ИССЛЕДОВАНИЯ Презентация по физике "Ток в газах" - скачать
Презентация по физике "Ток в газах" - скачать  Строение вещества Презентация подготовлена учителем физики МБОУ Тихо-Журавская ООШ Ашихминой Ольгой Анатольевной
Строение вещества Презентация подготовлена учителем физики МБОУ Тихо-Журавская ООШ Ашихминой Ольгой Анатольевной  Расчет электростатических полей в вакууме
Расчет электростатических полей в вакууме Работы и вклад в развитие электротехники Николы Тесла
Работы и вклад в развитие электротехники Николы Тесла Проводники, Полупроводники и непроводники электрического тока
Проводники, Полупроводники и непроводники электрического тока Разъемные соединения. Резьбовые соединения. Типы резьб. Детали резьбовых соединений. Основные расчетные случаи. Виды разрушений
Разъемные соединения. Резьбовые соединения. Типы резьб. Детали резьбовых соединений. Основные расчетные случаи. Виды разрушений Внутренний фотоэффект в металлах
Внутренний фотоэффект в металлах Холодильная, криогенная техника и системы жизнеобеспечения
Холодильная, криогенная техника и системы жизнеобеспечения Аттестационная работа. Методы решения задач по физике. (10-11 класс)
Аттестационная работа. Методы решения задач по физике. (10-11 класс) Постоянный электрический ток
Постоянный электрический ток Властивості моделей. Симетрія у фізиці
Властивості моделей. Симетрія у фізиці Допустимі навантаження на грунт. Методи кількісної оцінки ступеня стійкості укосів і схилів. (Лекція 8)
Допустимі навантаження на грунт. Методи кількісної оцінки ступеня стійкості укосів і схилів. (Лекція 8)