Содержание
- 2. ФАЗОВАЯ СКОРОСТЬ Плоская монохроматическая волна с амплитудой А, частотой ω и волновым вектором k может быть
- 3. Продифференцируем (6.2) по времени: откуда , где - фазовая скорость. По формулам (5.2) и (5.3) находим:
- 4. Суперпозиция волн Рассмотренная выше плоская монохроматическая волна представляет собой строго периодический процесс, бесконечно протяженный в пространстве
- 5. Образование волновой группы Рассмотрим простейший случай: суперпозицию двух волн распространяющихся вдоль оси x. Будем считать, что
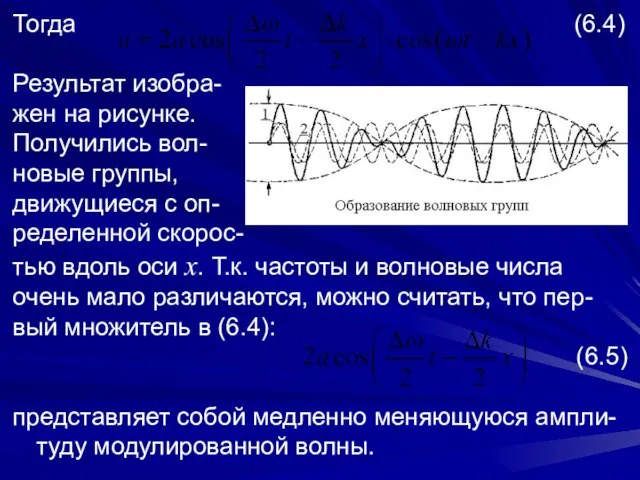
- 6. Тогда (6.4) Результат изобра- жен на рисунке. Получились вол- новые группы, движущиеся с оп- ределенной скорос-
- 7. ГРУППОВАЯ СКОРОСТЬ Скорость перемещения волновой группы - это ско-рость перемещения определенной амплитуды. Для ее определения запишем
- 8. ГРУППОВАЯ СКОРОСТЬ ВОЛН ДЕ-БРОЙЛЯ Для волн де-Бройля: (6.8) Таким образом, "обычная", т.е. измеряемая в эксперименте скорость
- 9. СООТНОШЕНИЕ МЕЖДУ ФАЗОВОЙ И ГРУППОВОЙ СКОРОСТЬЮ ВОЛН ДЕ-БРОЙЛЯ Вернемся к формуле (6.3) и запишем ее в
- 10. ВОЛНОВОЙ ПАКЕТ Путем наложения (супер- позиции) плоских волн с непрерывно меняющими- ся волновыми числами можно осуществить
- 11. ВОЛНОВОЙ ПАКЕТ Вследствие непрерывного изменения волнового чи-сла k сложение волн представляется интегралом (6.10) где амплитуду a
- 12. ВОЛНОВОЙ ПАКЕТ Для малого интервала Δk в формуле (6.11) мо-жно ограничиться первыми двумя членами разложения. Подставляя
- 13. ВОЛНОВОЙ ПАКЕТ Интеграл (6.12) легко вычисляется с помощью за-мены переменной. Обозначим тогда и интеграл (6.10) принимает
- 14. Подставляя пределы и умножая числитель и знаме-натель на Δk, получаем: (6.13) Этот результат можно интерпретировать так
- 15. Групповая скорость волнового пакета Обозначим: (6.15) Тогда формулу (6.14) можно записать в виде: (6.16) Таким образом,
- 16. Групповая скорость волнового пакета Итак, множитель при имеет максимум, равный 1. Скорость перемещения этого максиму-ма можно
- 17. Волновой пакет Итак, в результате суперпозиции волн получился волновой пакет с амплитудой примерный вид которой изображен
- 19. Скачать презентацию















 Летательный аппарат ракета
Летательный аппарат ракета Вводная лекция Лекция 1
Вводная лекция Лекция 1  Жарық дифракциясы. Френельдің аумақ әдісі. Жарықтың түзу сызықпен таралуы. Аумақ пластинасы
Жарық дифракциясы. Френельдің аумақ әдісі. Жарықтың түзу сызықпен таралуы. Аумақ пластинасы Автор: Данилова С.В., учитель начальных классов МОУ «Столипинская СОШ» Зубцовского района
Автор: Данилова С.В., учитель начальных классов МОУ «Столипинская СОШ» Зубцовского района FOURWINGS Дрон нового поколения
FOURWINGS Дрон нового поколения α - ыдырау
α - ыдырау Сверхпроводники настоящее и будущее
Сверхпроводники настоящее и будущее Геофизические исследования скважин. (Лекция 11)
Геофизические исследования скважин. (Лекция 11) Молекулярная физика
Молекулярная физика  Применение фотоэффекта в жизни
Применение фотоэффекта в жизни Презентация по физике "М.В.Ломоносов в области физики и астрономии" - скачать
Презентация по физике "М.В.Ломоносов в области физики и астрономии" - скачать  Методы сканирующей зондовой микроскопии. Электросиловая микроскопия. Тема 4
Методы сканирующей зондовой микроскопии. Электросиловая микроскопия. Тема 4 Сведение и обработка цифрового звукового сигнала
Сведение и обработка цифрового звукового сигнала Свободное падение
Свободное падение Поляризация диэлектриков
Поляризация диэлектриков Физика в моей специальности
Физика в моей специальности ИК-спектроскопия
ИК-спектроскопия Спектроскопы. Спектральный анализ
Спектроскопы. Спектральный анализ Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Основные характеристики атомных ядер. (Тема 1.1)
Основные характеристики атомных ядер. (Тема 1.1) Работу выполнила: Макарова Екатерина, ученица 7 класса, ГОУ СОШ № 546 г.Москвы Руководитель: Казакова Ю.В., учитель физики
Работу выполнила: Макарова Екатерина, ученица 7 класса, ГОУ СОШ № 546 г.Москвы Руководитель: Казакова Ю.В., учитель физики Авторы: М.Ю. Фризен, учитель физики В.В. Широких, учитель литературы
Авторы: М.Ю. Фризен, учитель физики В.В. Широких, учитель литературы Ядерная технология и технологии двойного назначения
Ядерная технология и технологии двойного назначения Упругие и пластические деформации. Закон Гука
Упругие и пластические деформации. Закон Гука Енергозбереження
Енергозбереження Материя и цвет. Свет
Материя и цвет. Свет Растяжение - сжатие
Растяжение - сжатие Ядерный реактор
Ядерный реактор