Содержание
- 2. О – начало координат (начало отсчёта); K – название системы отсчёта. Положение МТ в пространстве в
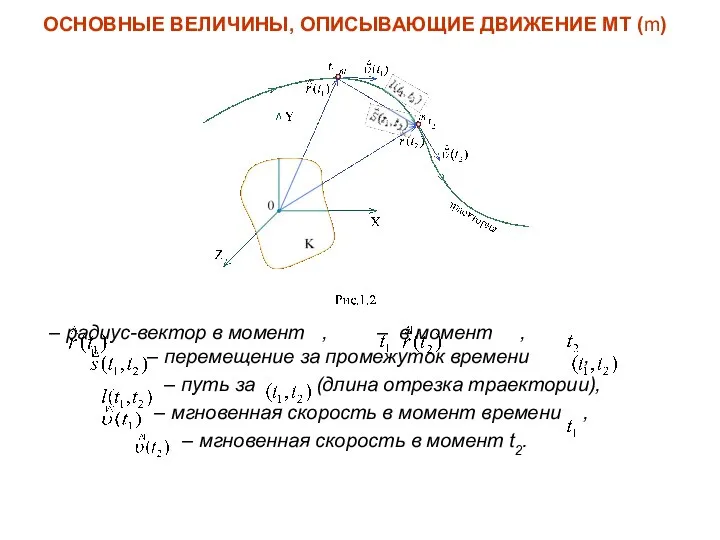
- 3. ОСНОВНЫЕ ВЕЛИЧИНЫ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ МТ (m) – радиус-вектор в момент , – в момент , –
- 4. PS. Векторы скорости и – касательные к траектории. Очевидно: . (1.4) При малых очевидно, что .
- 5. Мгновенная путевая скорость (при ): . (1.9) Или . (1.10) Из (1.5), (1.6), (1.7а), (1.8) и
- 6. Обратно: , выполняется с помощью интегрирования. Чтобы найти по заданной , необходимо знать начальное значение ;
- 7. Векторные равенства можно записать в проекциях на оси координат: , , (1.20а,б) , , (1.21а,б) ,
- 8. 1.2. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ НА ПЛОСКОСТИ. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ: ТАНГЕНЦИАЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ. Итак
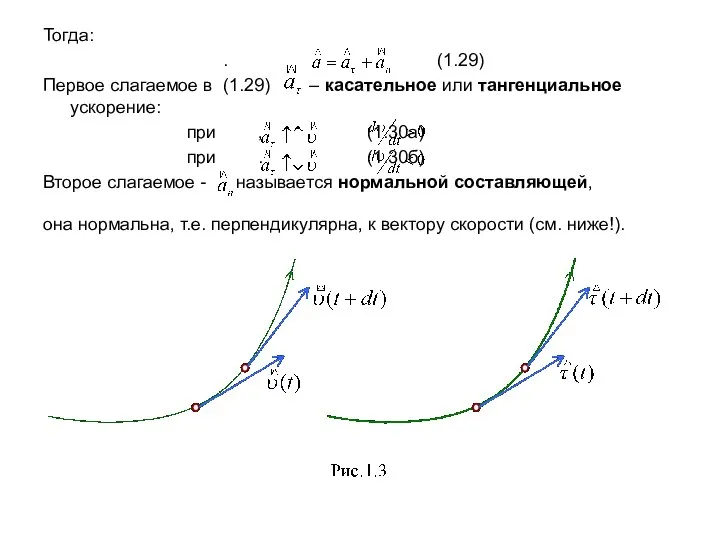
- 9. Тогда: . (1.29) Первое слагаемое в (1.29) – касательное или тангенциальное ускорение: при , (1.30а) при
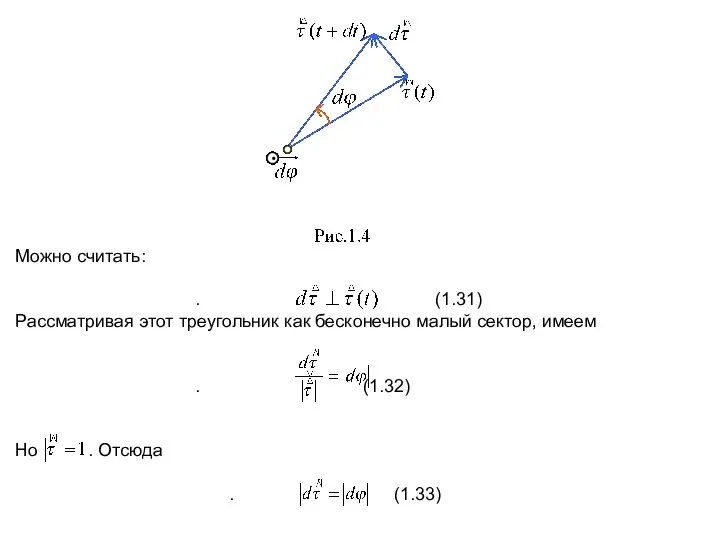
- 10. Можно считать: . (1.31) Рассматривая этот треугольник как бесконечно малый сектор, имеем . (1.32) Но .
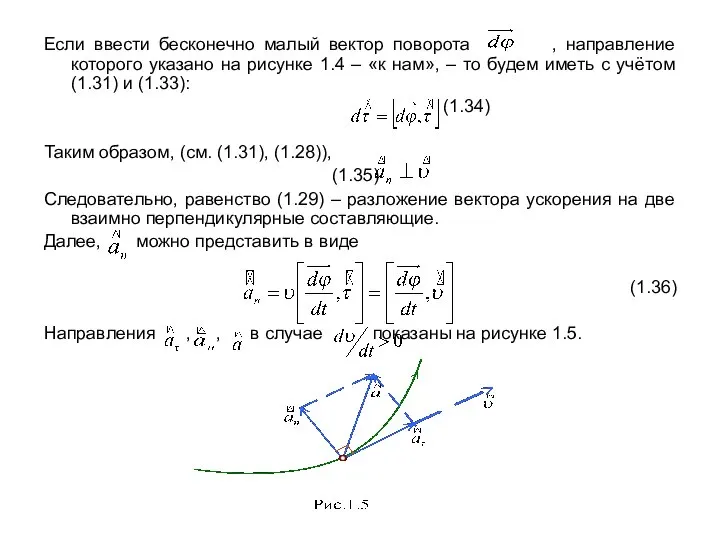
- 11. Если ввести бесконечно малый вектор поворота , направление которого указано на рисунке 1.4 – «к нам»,
- 12. Если считать малый отрезок криволинейной траектории частью окружности, то величина (1.37) называется вектором угловой скорости. Вектор
- 13. 1.3 НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ. СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМИ И УГЛОВЫМИ ВЕЛИЧИНАМИ.
- 14. Дифференцируя (1.41), находим ускорение: (1.42) Второе слагаемое в (1.42) ( см. (1.36) ) есть нормальное ускорение:
- 15. Теперь ускорение её запишется с учётом (1.41) в виде . (1.46) Двойное векторное произведение в (1.46)
- 16. Рассмотрим аналогию между ускоренными прямолинейным и криволинейным движениями (на примере МТ, движущейся по окружности). Ось OZ
- 17. Для движения по окружности: , . (1.52а, б) Равнопеременное движение вдоль оси описывается равенствами: , (1.53
- 19. Скачать презентацию












 Презентация Энергосбережение в быту
Презентация Энергосбережение в быту  New Technologies Could Make Interstellar Travel Real
New Technologies Could Make Interstellar Travel Real Физические свойства высокочастотных линий. Основные определения и классификация кабелей. Параметры линии
Физические свойства высокочастотных линий. Основные определения и классификация кабелей. Параметры линии Вечный двигатель Подготовила: ученица 7 Б класса Погуляева Ирина
Вечный двигатель Подготовила: ученица 7 Б класса Погуляева Ирина Теплопроводность при нестационарном тепловом режиме
Теплопроводность при нестационарном тепловом режиме Использование сенсорных систем в мобильной робототехнике
Использование сенсорных систем в мобильной робототехнике Устройство и история счетчиков электроэнергии
Устройство и история счетчиков электроэнергии Принцип относительности Галилея и электромагнитные явления
Принцип относительности Галилея и электромагнитные явления ЯМР спектроскопия. Основные вехи
ЯМР спектроскопия. Основные вехи Презентация по физике "Эксплуатация и хранение щелочных (алкалиновых) и солевых батареек" - скачать
Презентация по физике "Эксплуатация и хранение щелочных (алкалиновых) и солевых батареек" - скачать  Бегом по радуге. Игра-состязание по физике среди 8 классов
Бегом по радуге. Игра-состязание по физике среди 8 классов УРОК ФИЗИКИ В 10 КЛАССЕ Импульс тела. Закон сохранения
УРОК ФИЗИКИ В 10 КЛАССЕ Импульс тела. Закон сохранения Общие сведения из технической термодинамики
Общие сведения из технической термодинамики Physical basis of optic. Rieznyk
Physical basis of optic. Rieznyk Удивительные и странные свойства воды
Удивительные и странные свойства воды Теорема Остроградского-Гаусса
Теорема Остроградского-Гаусса Излучение электромагнитного поля. Антенны
Излучение электромагнитного поля. Антенны Скорость. Расчет пути и времени
Скорость. Расчет пути и времени Электрический заряд. Электризация. Закон сохранения заряда. Закон Кулона
Электрический заряд. Электризация. Закон сохранения заряда. Закон Кулона Радиоактивность. (9 класс)
Радиоактивность. (9 класс) Защита картера и КПП CHERY T19
Защита картера и КПП CHERY T19 Аттестационная работа. Творческая мастерская по физике
Аттестационная работа. Творческая мастерская по физике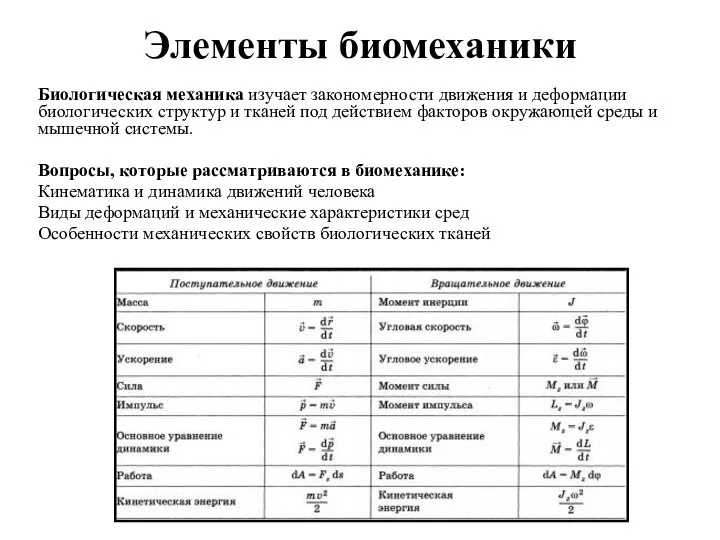 Элементы биомеханики. Деформация. (Лекция 2)
Элементы биомеханики. Деформация. (Лекция 2) 1.1 Классификация, структура и состав СЭЭС
1.1 Классификация, структура и состав СЭЭС Физико-химические свойства нефтей и нефтепродуктов
Физико-химические свойства нефтей и нефтепродуктов ГУ «Новопокровская средняя школа» Бородулихинского района, ВКО. Тест по теме: «Электрические заряды»
ГУ «Новопокровская средняя школа» Бородулихинского района, ВКО. Тест по теме: «Электрические заряды»  Оборудование и технология получения наноматериалов из газовой фазы
Оборудование и технология получения наноматериалов из газовой фазы Электромагниттік толќындар
Электромагниттік толќындар