Содержание
- 2. Основные типы краевых условий для изгибных колебаний стержней
- 3. В технической теории изгибные колебания стержня описывают уравнением при p = 0 Если стержень имеет постоянные
- 4. Для стержня, совершающего собственные изгибные колебания, решение может быть методом разделения переменных. Граничные условия для W(x)
- 5. Общее решение. Применение метода начальных параметров. Функции Крылова. Решением уравнения (10.3) является функция Представление общего решения
- 6. Собственные частоты и собственные формы колебаний. Для получения частотного уравнения необходимо привлечь краевые условия. Подстановка в
- 7. При решении большого класса задач удобно использовать фундаментальную систему Коши . Фундаментальной системой Коши в случае
- 8. Общее решение через функции Крылова имеет вид Аналог общего решения, соответствующий методу начальных параметров, имеет вид
- 9. Функции Крылова Sj (х) и их производные по x, как это следует из (10.8) и (10.7),
- 10. Собственные частоты и собственные формы колебаний. Для получения частотного уравнения необходимо привлечь краевые условия. Подстановка в
- 13. Скачать презентацию










 Применение законов физики в повседневной жизни
Применение законов физики в повседневной жизни Ядерно-химические свойства
Ядерно-химические свойства Max.Industries. Технология термоядерного реактора
Max.Industries. Технология термоядерного реактора Квантование момента импульса атома. Момент импульса многоэлектронных атомов
Квантование момента импульса атома. Момент импульса многоэлектронных атомов Измерение сопротивления изоляции постоянному току
Измерение сопротивления изоляции постоянному току Тепловое излучение
Тепловое излучение Внутренняя энергия и способы ее изменения
Внутренняя энергия и способы ее изменения Теплові двигуни та охорона навколишнього середовища
Теплові двигуни та охорона навколишнього середовища  Проект Эко-солнце г. Королев 2014 год
Проект Эко-солнце г. Королев 2014 год Открытие нейтрона
Открытие нейтрона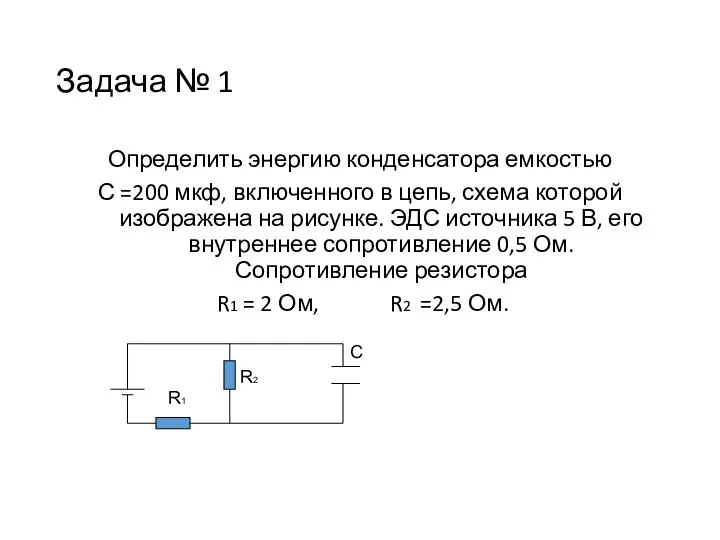 Конденсаторы в цепи постоянного тока
Конденсаторы в цепи постоянного тока Резисторы. Основные параметры резисторов
Резисторы. Основные параметры резисторов Презентация по физике "Изопроцессы" - скачать
Презентация по физике "Изопроцессы" - скачать  Презентация по физике "Приручение огня" - скачать бесплатно
Презентация по физике "Приручение огня" - скачать бесплатно Тема урока Приложения определенного интеграла к решению физических задач
Тема урока Приложения определенного интеграла к решению физических задач Елементи режимів різання. Визначення режимів різання. Тема 8
Елементи режимів різання. Визначення режимів різання. Тема 8 Детали машин и основы конструирования. Лекция №4
Детали машин и основы конструирования. Лекция №4 Електричний заряд. Електростатичне поле. Конденсатори
Електричний заряд. Електростатичне поле. Конденсатори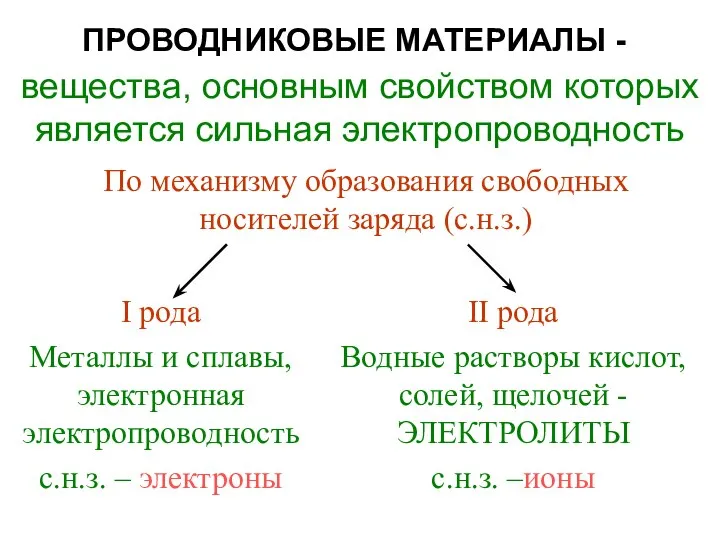 Проводниковые материалы
Проводниковые материалы Обертальний рух твердого тіла
Обертальний рух твердого тіла Класифікація та моделі сигналів та систем. (Лекція 1)
Класифікація та моделі сигналів та систем. (Лекція 1) Избавляемся от статического электричества (Фрагмент урока по теме «Электризация тел») Выполнила Васильева Марина Викторовн
Избавляемся от статического электричества (Фрагмент урока по теме «Электризация тел») Выполнила Васильева Марина Викторовн Газовые законы (10 класс) - Презентация по физике_
Газовые законы (10 класс) - Презентация по физике_ Электрические системы
Электрические системы Электростатическое поле в вакууме
Электростатическое поле в вакууме Элементы квантовой статистики и физики твёрдого тела. Лекция № 6. Часть 1
Элементы квантовой статистики и физики твёрдого тела. Лекция № 6. Часть 1 Своя игра
Своя игра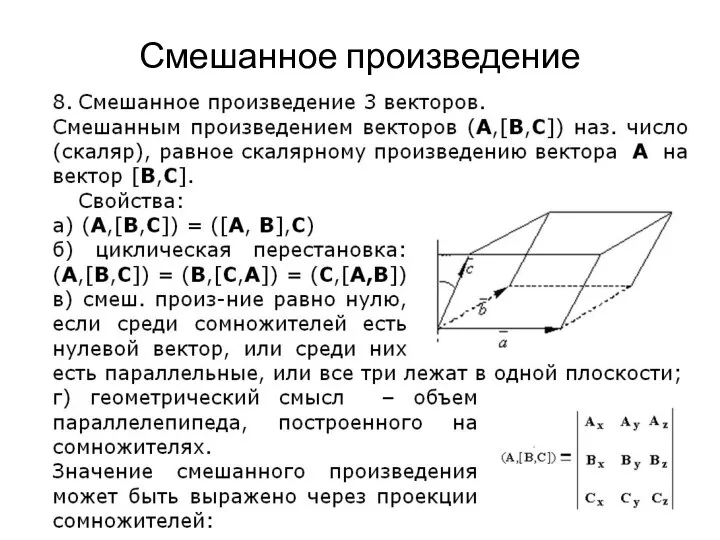 Основы кинематики и динамики
Основы кинематики и динамики