Содержание
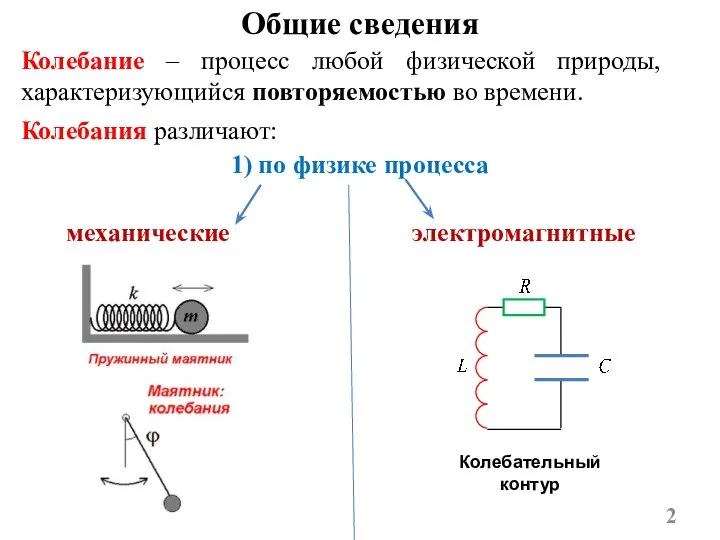
- 2. Колебание – процесс любой физической природы, характеризующийся повторяемостью во времени. Колебания различают: 1) по физике процесса
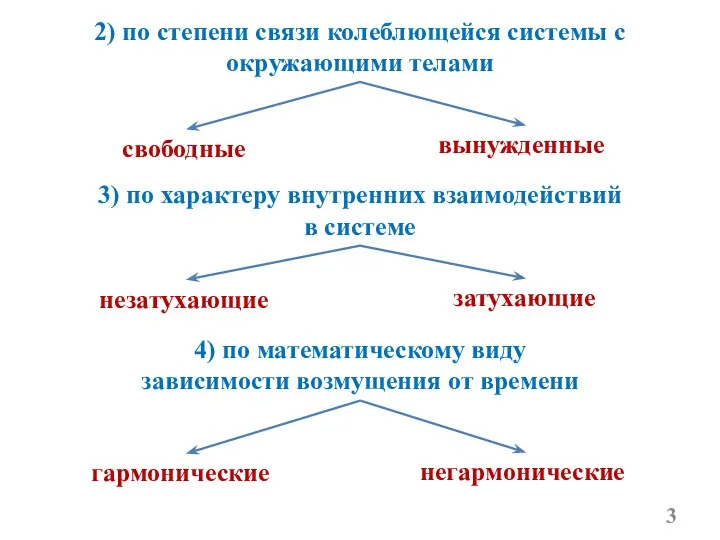
- 3. 2) по степени связи колеблющейся системы с окружающими телами затухающие незатухающие 3) по характеру внутренних взаимодействий
- 4. Период колебания T [c] – временной интервал, в течение которого совершается одно полное колебание. Периодическое колебание
- 5. СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Гармонические колебания – периодическое изменение физической величины во времени, протекающее по закону синуса
- 6. Гармонические колебания величины x описываются уравнением вида: A – амплитуда колебания. (ω0t+φ) – фаза гармонического колебания
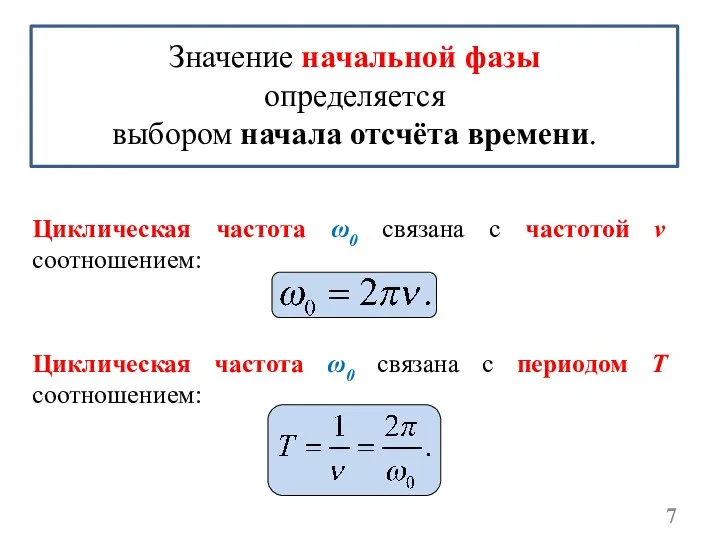
- 7. Значение начальной фазы определяется выбором начала отсчёта времени. Циклическая частота ω0 связана с частотой ν соотношением:
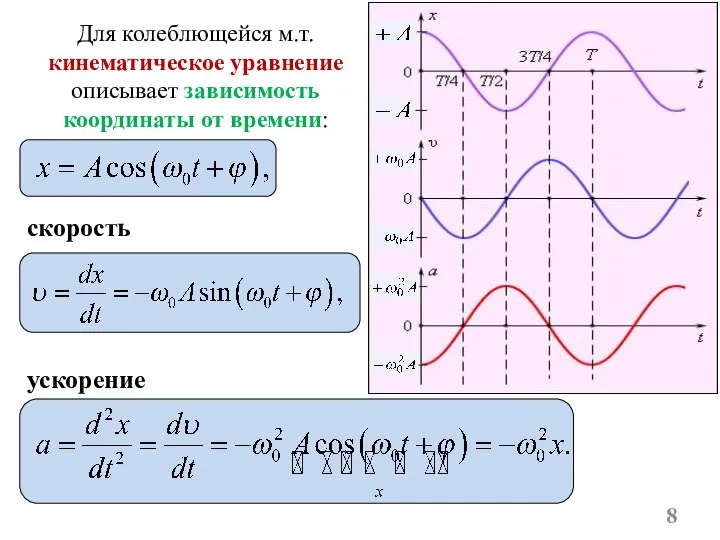
- 8. скорость ускорение Для колеблющейся м.т. кинематическое уравнение описывает зависимость координаты от времени:
- 9. Это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой
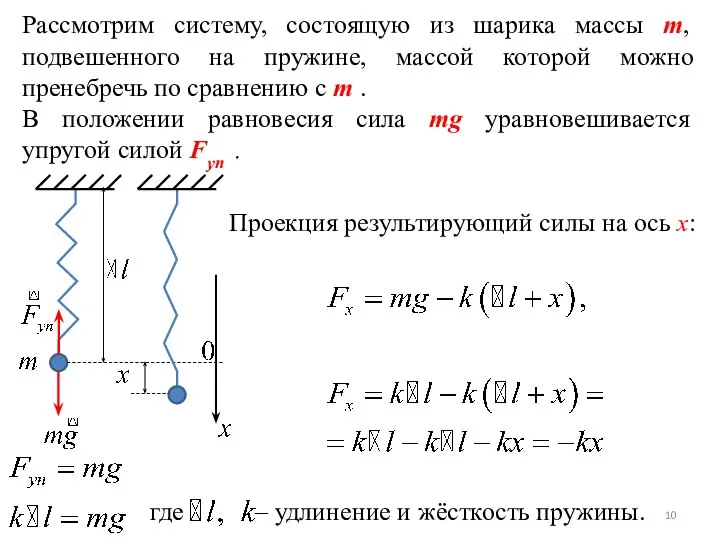
- 10. Рассмотрим систему, состоящую из шарика массы m, подвешенного на пружине, массой которой можно пренебречь по сравнению
- 11. Уравнение движения маятника в отсутствие сил трения описывается дифференциальным уравнением: Пружинный маятник совершает гармонические колебания с
- 12. Гармонический осциллятор – систем, совершающая колебания, описываемые уравнением вида
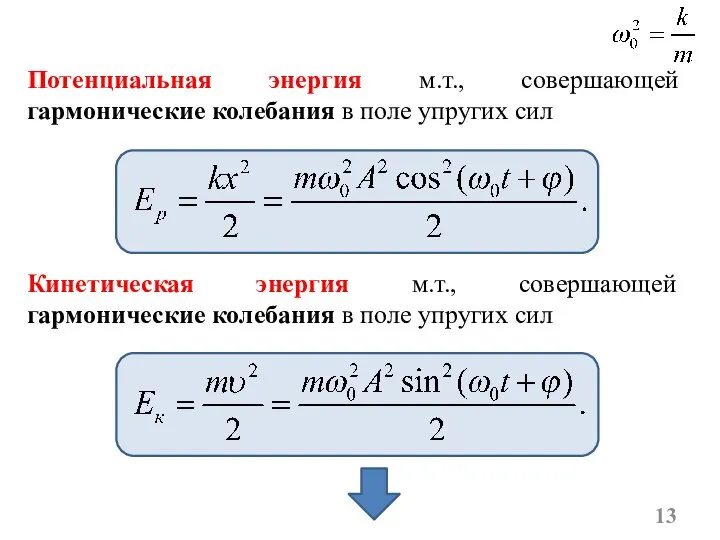
- 13. Потенциальная энергия м.т., совершающей гармонические колебания в поле упругих сил Кинетическая энергия м.т., совершающей гармонические колебания
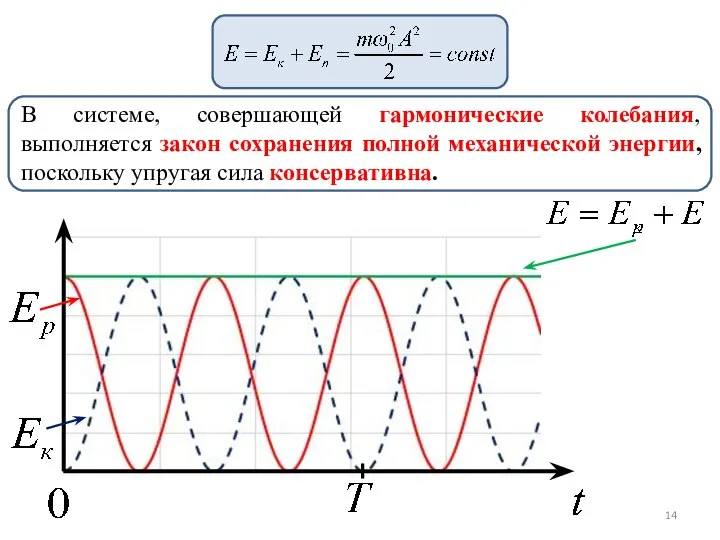
- 14. В системе, совершающей гармонические колебания, выполняется закон сохранения полной механической энергии, поскольку упругая сила консервативна.
- 15. 2. Физический маятник Это твёрдое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси
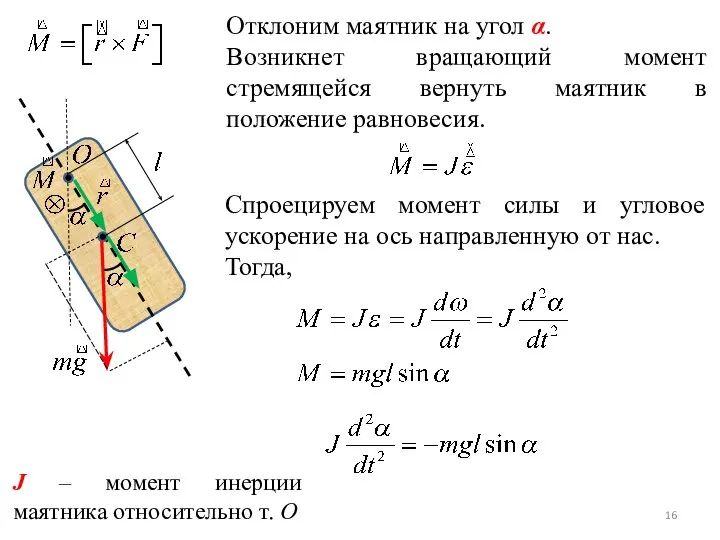
- 16. Отклоним маятник на угол α. Возникнет вращающий момент стремящейся вернуть маятник в положение равновесия. Спроецируем момент
- 17. При малых отклонениях Решением данного дифференциального уравнения будет функция вида - период колебания физического маятника.
- 18. Это идеализированная система, состоящая из м.т. массой m, подвешенной на нерастяжимой нити, и колеблющаяся под действием
- 19. Свободные гармонические колебания в колебательном контуре Электромагнитные колебания – колебания, при которых электрические величины (заряды, токи)
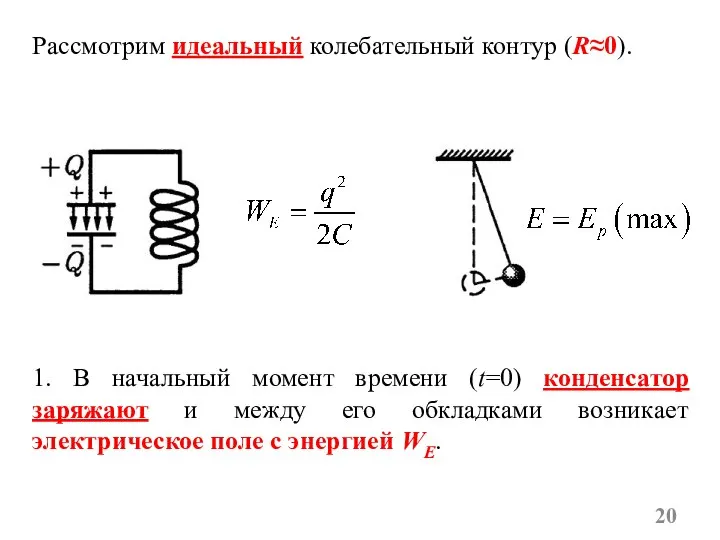
- 20. Рассмотрим идеальный колебательный контур (R≈0). 1. В начальный момент времени (t=0) конденсатор заряжают и между его
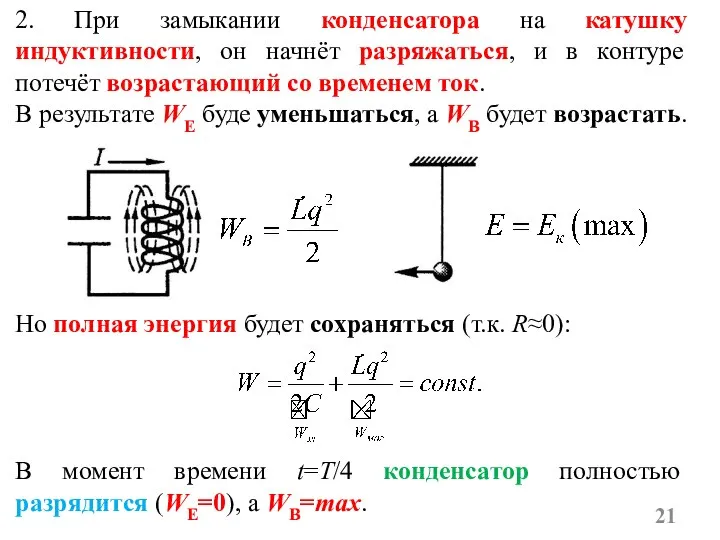
- 21. 2. При замыкании конденсатора на катушку индуктивности, он начнёт разряжаться, и в контуре потечёт возрастающий со
- 22. 3. Затем ток начнет убывать (магнитное поле катушки будет ослабевать, что будет способствовать появлению индукционного тока,
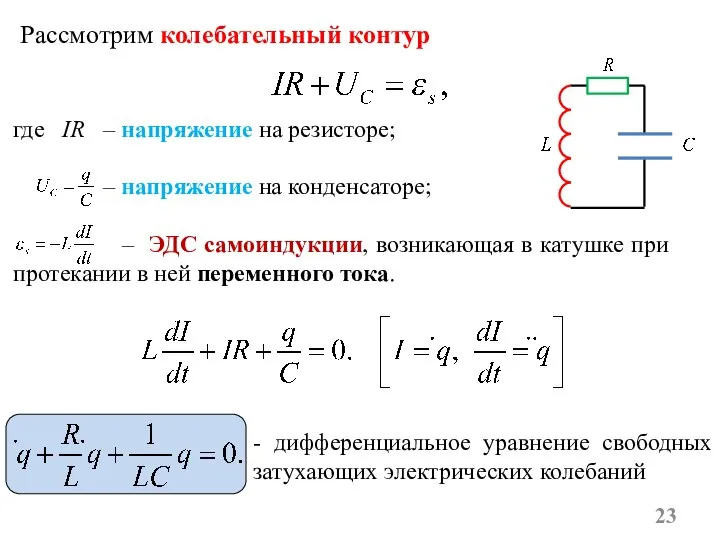
- 23. Рассмотрим колебательный контур где IR – напряжение на резисторе; – напряжение на конденсаторе; – ЭДС самоиндукции,
- 24. В данном колебательном контуре отсутствуют внешние ЭДС, поэтому такие колебания называются свободными. Если R=0, то свободные
- 25. и периодом Формула Томпсона где Imax – амплитуда силы тока. где Umax – амплитуда напряжения. Вывод:
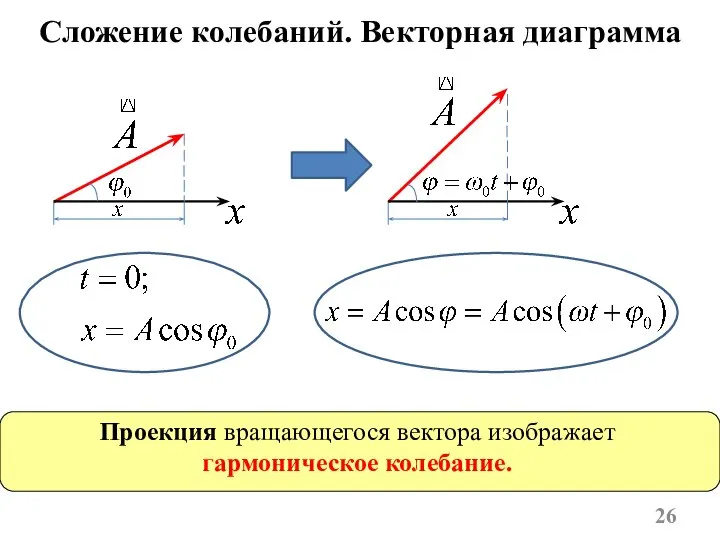
- 26. Сложение колебаний. Векторная диаграмма Проекция вращающегося вектора изображает гармоническое колебание.
- 27. Сложение гармонических колебаний Рассмотрим однонаправленные одночастотные колебания с неизменными амплитудами и постоянной разностью начальных фаз. Когерентность
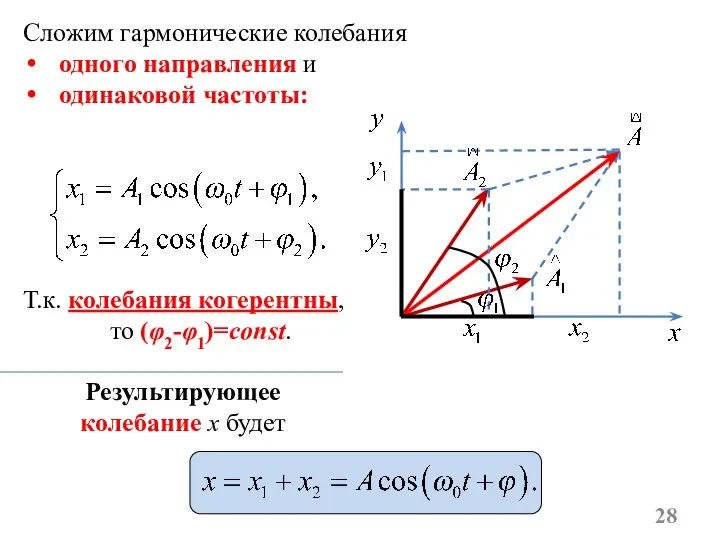
- 28. Сложим гармонические колебания одного направления и одинаковой частоты: Т.к. колебания когерентны, то (φ2-φ1)=const. Результирующее колебание x
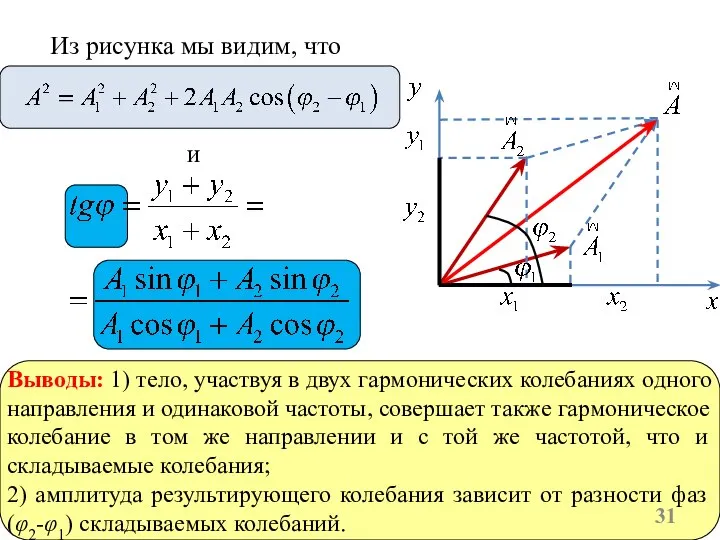
- 31. Из рисунка мы видим, что и Выводы: 1) тело, участвуя в двух гармонических колебаниях одного направления
- 32. Рассмотрим выражение (4) В этом случае A=A1+A2, т.е. амплитуда результирующего колебания A равна сумме амплитуд складываемых
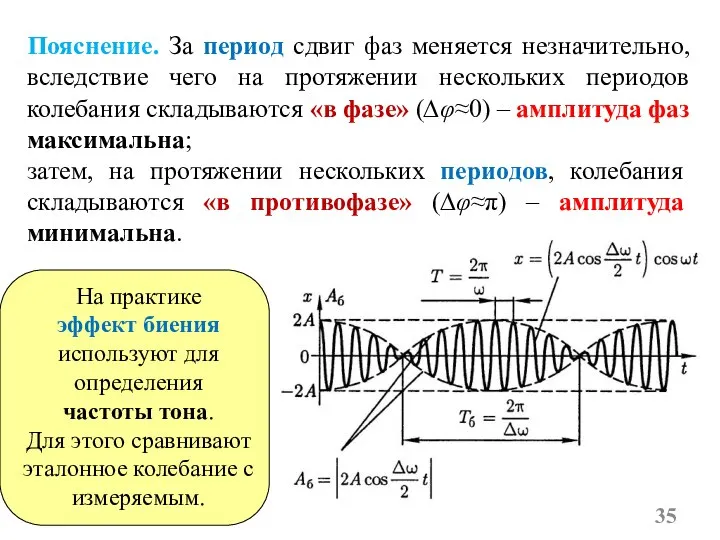
- 33. Биения Биения – периодические изменения амплитуды колебаний, возникающие при сложении двух гармонических колебаний с близкими частотами.
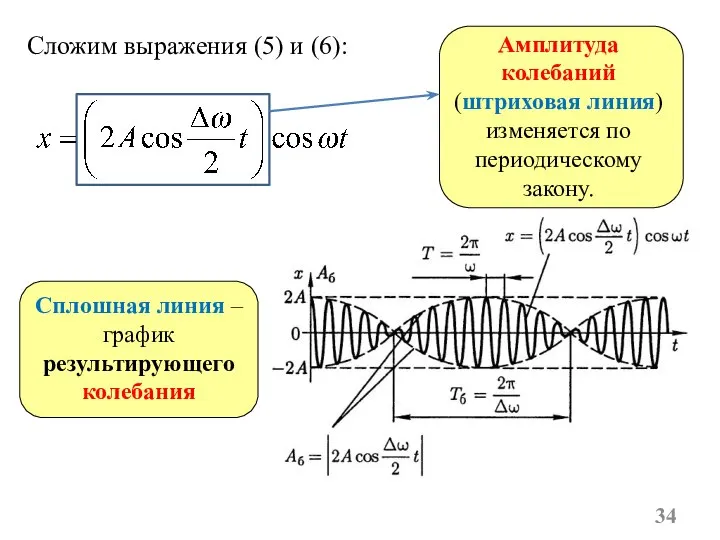
- 34. Сложим выражения (5) и (6): Амплитуда колебаний (штриховая линия) изменяется по периодическому закону. Сплошная линия –
- 35. Пояснение. За период сдвиг фаз меняется незначительно, вследствие чего на протяжении нескольких периодов колебания складываются «в
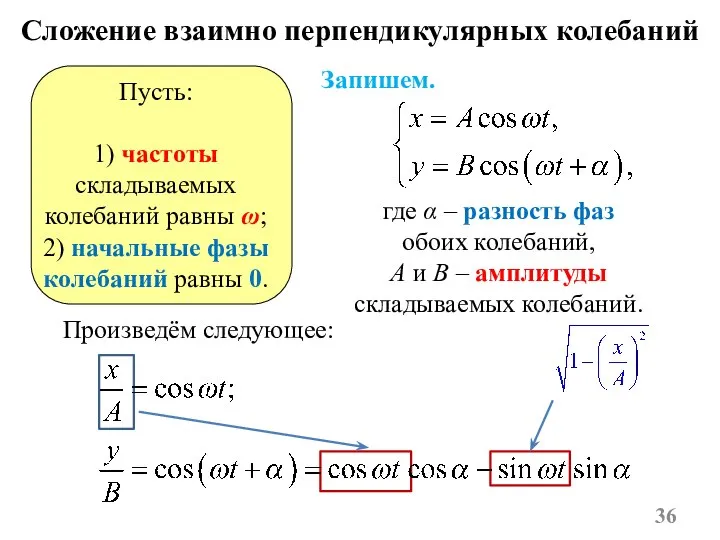
- 36. Сложение взаимно перпендикулярных колебаний Запишем. где α – разность фаз обоих колебаний, A и B –
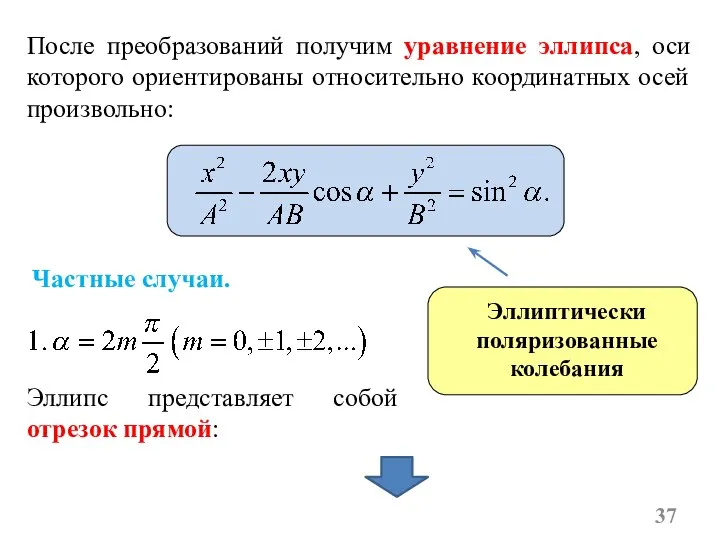
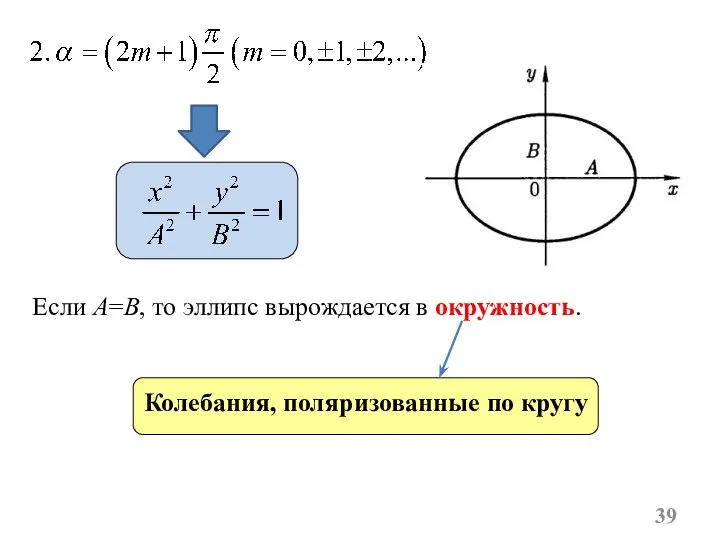
- 37. После преобразований получим уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно: Эллиптически поляризованные колебания Частные
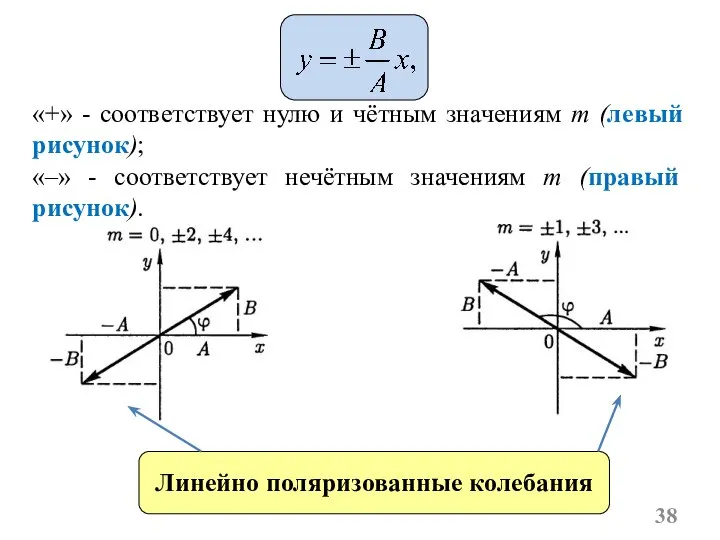
- 38. Линейно поляризованные колебания «+» - соответствует нулю и чётным значениям m (левый рисунок); «–» - соответствует
- 39. Колебания, поляризованные по кругу Если A=B, то эллипс вырождается в окружность.
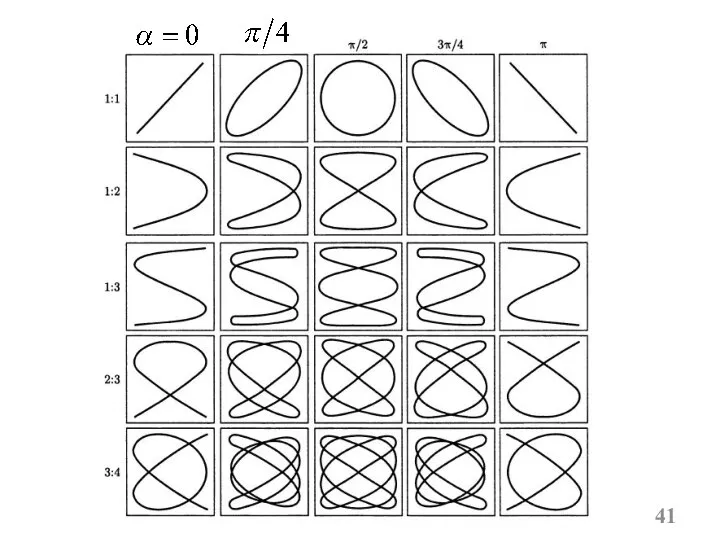
- 40. Вид кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. 3. При различных частотах
- 42. Свободные затухающие колебания Затухающие колебания – колебания, амплитуды которых из-за потерь энергии колебательной системы с течением
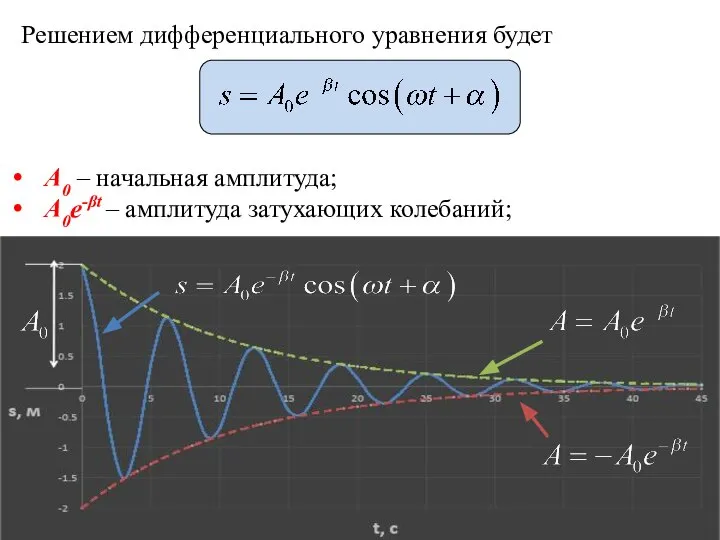
- 43. Решением дифференциального уравнения будет A0 – начальная амплитуда; A0e-βt – амплитуда затухающих колебаний;
- 44. Время релаксации – время, в течение которого амплитуда затухающих колебаний уменьшается в е раз. Затухающие колебания
- 45. Декрементом затухания называют отношение амплитуд двух последовательных колебаний, соответствующих моментам времени, отличающихся на период. Логарифмический декремент
- 46. Добротность колебательной системы пропорциональна числу колебаний Ne, совершаемых системой за то время τ, за которое амплитуда
- 48. Скачать презентацию
![Период колебания T [c] – временной интервал, в течение которого совершается](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/740414/slide-3.jpg)














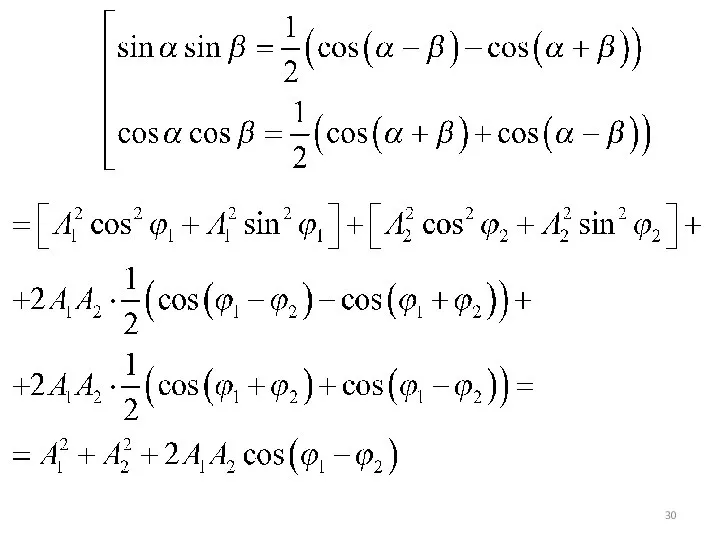







 Презентация по физике "Електромагнітні хвилі в природі і техніці" - скачать
Презентация по физике "Електромагнітні хвилі в природі і техніці" - скачать  Контроль и диагностика
Контроль и диагностика Большой адронный коллайдер
Большой адронный коллайдер Презентация по физике Двигатели внутреннего сгорания
Презентация по физике Двигатели внутреннего сгорания  Поперечные и продольные волны
Поперечные и продольные волны Крокова напруга
Крокова напруга Газоразрядные источники оптического излучения для возбуждения активных сред лазеров
Газоразрядные источники оптического излучения для возбуждения активных сред лазеров Сверхминиатюрные излучатели на основе полупроводниковых наноструктур
Сверхминиатюрные излучатели на основе полупроводниковых наноструктур Ремонт автомобилей. Восстановление деталей слесарно-механической обработкой. (Тема 3.2)
Ремонт автомобилей. Восстановление деталей слесарно-механической обработкой. (Тема 3.2) Режимы работы электродвигателей. Лекция №11
Режимы работы электродвигателей. Лекция №11 Электромагниттік толқындар шкаласы. Сәулелену жазығы шакласы
Электромагниттік толқындар шкаласы. Сәулелену жазығы шакласы Средства измерений и их основные элементы
Средства измерений и их основные элементы Кинетика химических реакций. Лабораторная работа № 5
Кинетика химических реакций. Лабораторная работа № 5 Явления переноса в газах. (Лекция 3)
Явления переноса в газах. (Лекция 3) История гироскопии
История гироскопии Магнитное поле и его графическое изображение. Неоднородное и однородное магнитное поле
Магнитное поле и его графическое изображение. Неоднородное и однородное магнитное поле Андре-Марі Ампер Роботу виконала Учениця 10-а класу Макарівського НВК Заріцька Вікторія
Андре-Марі Ампер Роботу виконала Учениця 10-а класу Макарівського НВК Заріцька Вікторія  Анализ предельных возможностей и свойств исследуемой модели подводного аппарата (ПА), как объекта оптимального управления
Анализ предельных возможностей и свойств исследуемой модели подводного аппарата (ПА), как объекта оптимального управления Сила тяжести. Вес тела. Сила упругости. Решение задач
Сила тяжести. Вес тела. Сила упругости. Решение задач Презентация по физике "Инфразвук и ультразвук" - скачать
Презентация по физике "Инфразвук и ультразвук" - скачать  Практическая работа по биофизике
Практическая работа по биофизике Возможности восстановления смазанных космических изображений
Возможности восстановления смазанных космических изображений Магнитное поле. Вектор магнитной индукции
Магнитное поле. Вектор магнитной индукции Некоторые вопросы физики магнитных явлений
Некоторые вопросы физики магнитных явлений Модель флюгерного оконного генератора для вырабатывания электрического тока
Модель флюгерного оконного генератора для вырабатывания электрического тока Колебания систем с одной степенью свободы
Колебания систем с одной степенью свободы Приборы для измерения давления
Приборы для измерения давления Жидкости. Строение и свойства жидкостей
Жидкости. Строение и свойства жидкостей