Колебания систем с одной степенью свободы

Август 9, 2022

Главная
Физика
Колебания систем с одной степенью свободы

Содержание

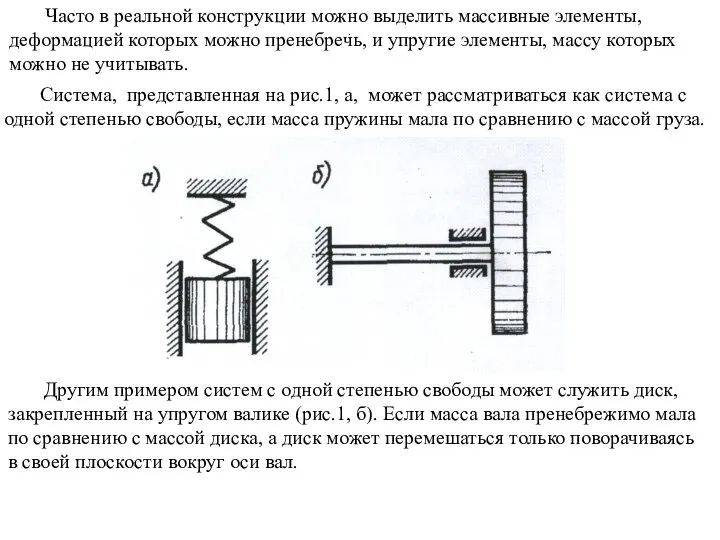
2. Часто в реальной конструкции можно выделить массивные элементы, деформацией которых можно пренебречь, и упругие элементы, массу
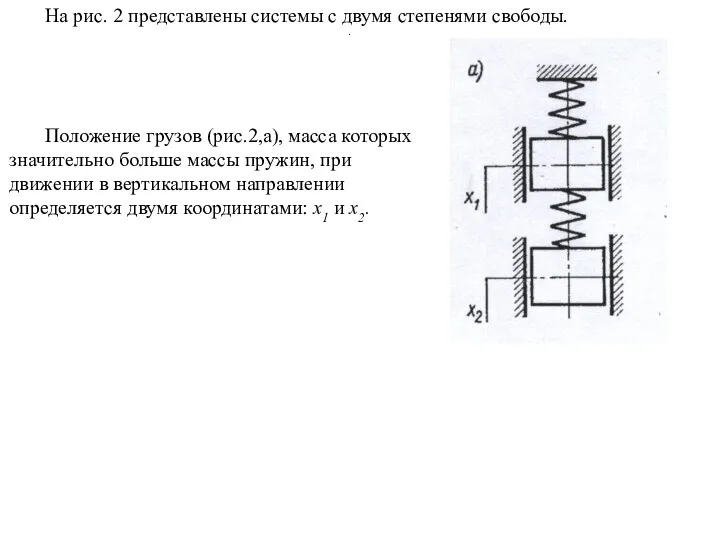
3. На рис. 2 представлены системы с двумя степенями свободы. Положение грузов (рис.2,а), масса которых значительно больше
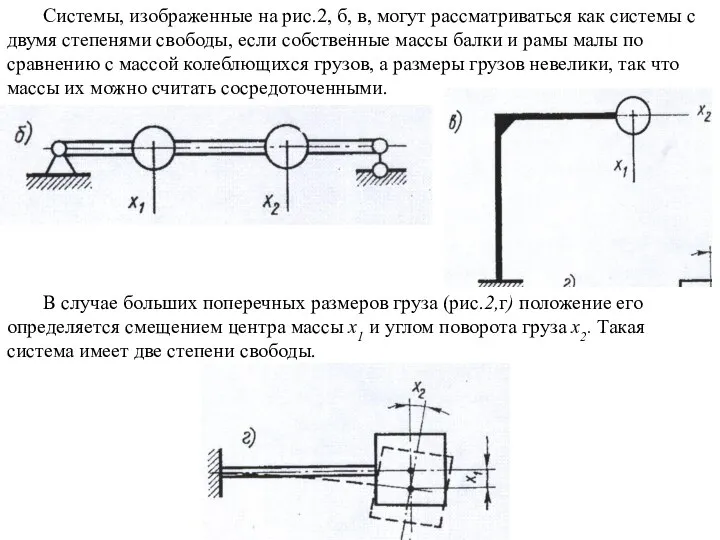
4. Системы, изображенные на рис.2, б, в, могут рассматриваться как системы с двумя степенями свободы, если собственные
5. Определение собственной частоты системы с одной степенью свободы 1. Записать кинетическую и потенциальную энергию системы соответственно
6. 6. Определить собственную частоту колебаний Если ввести f = k -1 - единичную податливость, соответствующую квазиупругому
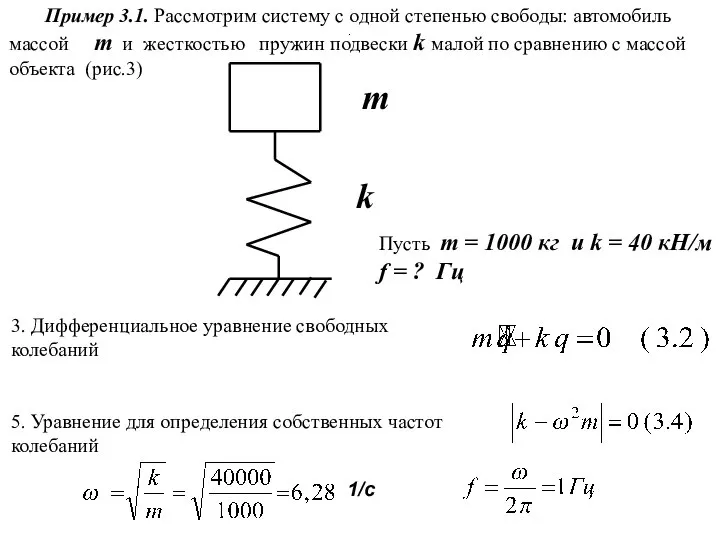
7. Пример 3.1. Рассмотрим систему с одной степенью свободы: автомобиль массой m и жесткостью пружин подвески k
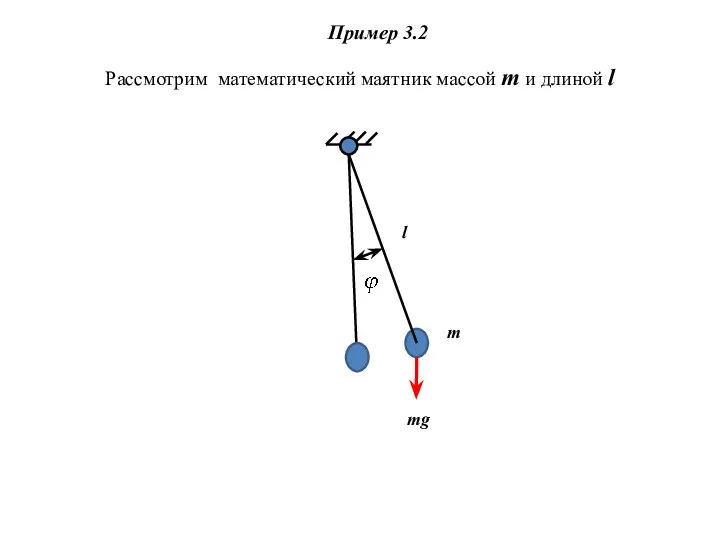
8. Пример 3.2 Рассмотрим математический маятник массой m и длиной l l m mg
9. Математический маятник Фуко в Национальном соборе г. Мехико
10. 1. Кинетическая и потенциальная энергия для математического маятника массой m и длиной l : - угол
11. Вычисляем собственную частоту свободных колебания маятника Пусть l = 98,1 м f = 0,05 Гц Т=
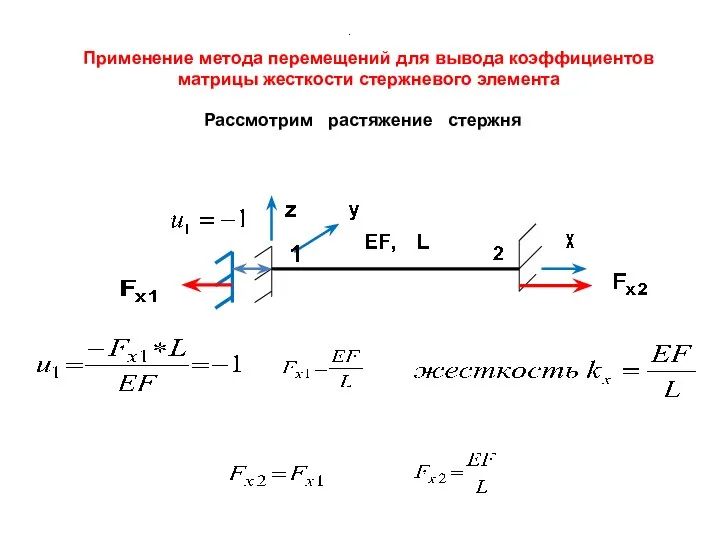
12. Рассмотрим растяжение стержня Применение метода перемещений для вывода коэффициентов матрицы жесткости стержневого элемента
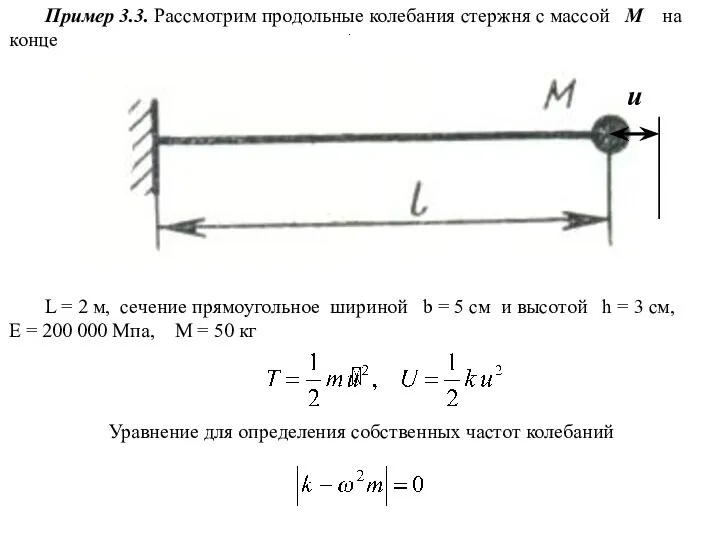
13. Пример 3.3. Рассмотрим продольные колебания стержня с массой М на конце L = 2 м, сечение
14. L = 2 м, сечение прямоугольное шириной b = 5 см и высотой h = 3
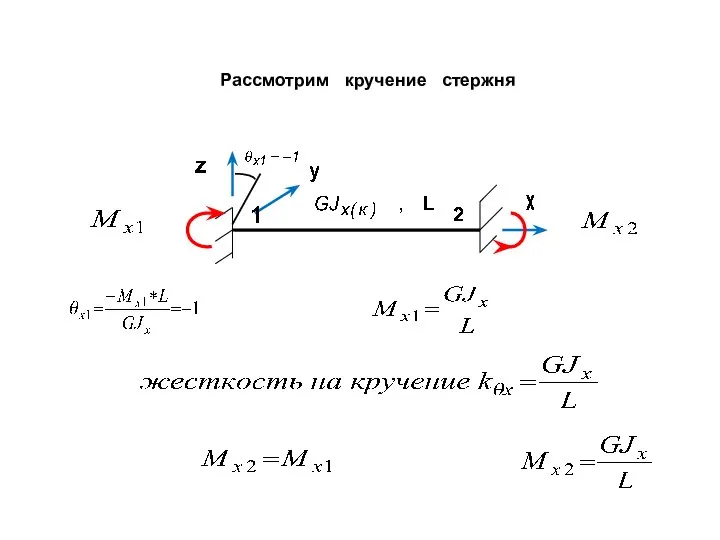
15. Рассмотрим кручение стержня
16. Iх = MR2 /2 Пример 3.4. Рассмотрим крутильные колебания вала с диском на конце с моментом
18. Скачать презентацию

Слайд 2

Часто в реальной конструкции можно выделить массивные элементы, деформацией которых можно

пренебречь, и упругие элементы, массу которых можно не учитывать.

Другим примером систем с одной степенью свободы может служить диск, закрепленный на упругом валике (рис.1, б). Если масса вала пренебрежимо мала по сравнению с массой диска, а диск может перемешаться только поворачиваясь в своей плоскости вокруг оси вал.

Система, представленная на рис.1, а, может рассматриваться как система с одной степенью свободы, если масса пружины мала по сравнению с массой груза.

Слайд 3

На рис. 2 представлены системы с двумя степенями свободы.
Положение грузов

(рис.2,а), масса которых значительно больше массы пружин, при движении в вертикальном направлении определяется двумя координатами: х1 и х2.

Слайд 4

Системы, изображенные на рис.2, б, в, могут рассматриваться как системы с

двумя степенями свободы, если собственные массы балки и рамы малы по сравнению с массой колеблющихся грузов, а размеры грузов невелики, так что массы их можно считать сосредоточенными.

В случае больших поперечных размеров груза (рис.2,г) положение его определяется смещением центра массы х1 и углом поворота груза х2. Такая система имеет две степени свободы.

Слайд 5