Определение продолжительности нагрева термически массивных тел. Аналитические методы определения времени нагрева

1. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ НАГРЕВА ИЗ АНАЛИТИЧЕСКОГО РЕШЕНИЯ КЗТ

1.1. ДОПУЩЕНИЯ

1) Реальные тела сводим к одному из тел правильной формы.

2) Граничные условия однородны по поверхности тела.

В результате этих двух допущений – симметричность и одномерность температурного поля:

3) Физические свойства не зависят от температуры.

4) Начальные и граничные условия описываются простейшими уравнениями.

(в общем случае

).

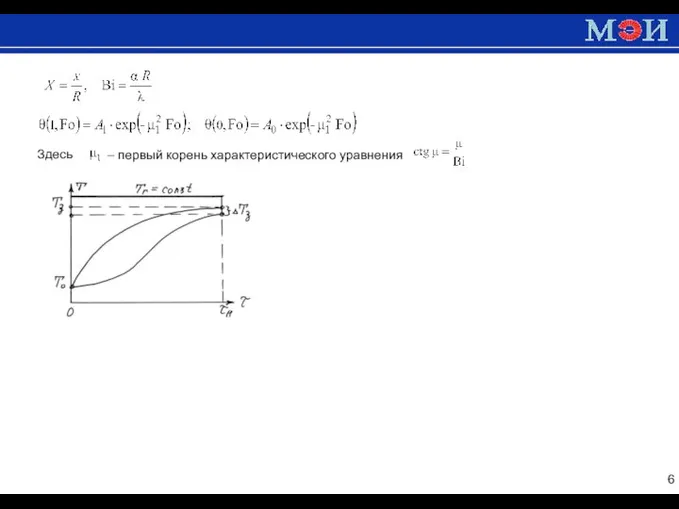
Следовательно, длительность нагрева приближенно равна длительности регулярного периода:

2. Геометрические условия задачи:

;

– характерный размер.

3. Физические условия задачи:

4. Начальные и граничные условия. ГУ:

Начальные условия (НУ):

1.3. РЕШЕНИЯ УРАВНЕНИЯ ФУРЬЕ

Случай 1:

(ГУ 2 рода).

Скорость подъема температуры во всех точках тела одинакова, перепад температур по толщине

.

Случай 2:

(ГУ 1 рода).

Начальные условия (НУ):

– перепад температур по всему характерному размеру.

Пластина

:

Случай 3:

(ГУ 3 рода).

ГУ:

НУ:

Для пластины решение имеет вид (регулярный режим!):