Содержание
- 2. Интеграл по замкнутому криволинейному контуру можно записать в декартовых координатах и применить формулу Стокса: Введя местную
- 3. Уравнение Эйлера Для плоского установившегося движения идеальной жидкости: Введя обозначение модуля скорости: w2 = u2 +
- 4. Уравнение Бернулли Проинтегрировав уравнение при ρ = const, получим уравнение для несжимаемой жидкости: Бернулли получил это
- 5. Рассмотрим плоское установившееся безвихревое движение Для безвихревого движения можно ввести потенциал скорости являющийся функцией φ(x, y),
- 6. Линия в жидкости, касательная к которой в любой ее точке параллельна направлению скорости, называется линией тока.
- 7. Рассмотрим сетку, образованную семейством линий тока ψ = const и линий равного потенциала φ = const.
- 8. Жидкость не может пересекать границу твердого тела, а значит проекция скорости на нормаль к поверхности ,
- 9. Примеры простейших потенциальных потоков Источник жидкости: комплексный потенциал Для удобства применим полярные координаты для комплексной переменной:
- 10. Комплексный потенциал вихря Линии тока – окружности, Линии равного потенциала - лучи. Окружная скорость жидкости Величина
- 11. Комплексный потенциал диполя , где q – момент диполя. Для удобства используем декартову СК: Приняв ψ
- 12. Потенциал обтекания окружности: Состоит из: плоскопараллельного потока диполя q = , вихря В полярной СК функции
- 13. Обтекание плоским потоком произвольного тела Выделим на контрольной поверхности S элементарную площадку ds*l и проведем к
- 14. Когда скорость невозмущенного потока направлена по оси ОХ и равна V∞, потенциал скорости можно записать в
- 15. Для определения силы лобового сопротивления тела X и подъемной силы У необходимо знать давление и скорость
- 16. Теорема Жуковского (1905г.) Если поток, имеющий в бесконечности скорость V∞, обтекает контур, и цирку-ляция скорости по
- 18. Скачать презентацию















 Електричний струм. Початок. Луїджи Гальвані (1737-1798) Досліди з препарованою жабою Поява терміну “гальванічний елемент”
Електричний струм. Початок. Луїджи Гальвані (1737-1798) Досліди з препарованою жабою Поява терміну “гальванічний елемент”  Выбор начальных и конечных параметров термодинамического цикла
Выбор начальных и конечных параметров термодинамического цикла Деформації. Сили пружності
Деформації. Сили пружності Разработка адаптивного метода оценки характеристик досмотровых комплексов с функцией распознавания материалов объектов контрол
Разработка адаптивного метода оценки характеристик досмотровых комплексов с функцией распознавания материалов объектов контрол Подготовка к муниципальному этапу по физике. Ассоциация победителей олимпиад. (11 класс)
Подготовка к муниципальному этапу по физике. Ассоциация победителей олимпиад. (11 класс) Внутренний мир светового луча
Внутренний мир светового луча Полеты в космос. Оперативное управление космическими аппаратами
Полеты в космос. Оперативное управление космическими аппаратами Радиационная биофизика. Часть 1
Радиационная биофизика. Часть 1 Презентация по физике "Электрический ток в газах" - скачать
Презентация по физике "Электрический ток в газах" - скачать  Презентація на тему «Ядерна Енергетика» Виконала учениця 11-А класу Родзінська Тетяна
Презентація на тему «Ядерна Енергетика» Виконала учениця 11-А класу Родзінська Тетяна  Курс загальної фізики. Лекція 2. Динаміка матеріальної точки і системи матеріальних точок динаміка обертального руху
Курс загальної фізики. Лекція 2. Динаміка матеріальної точки і системи матеріальних точок динаміка обертального руху Гелиоцентрическая система мира
Гелиоцентрическая система мира Электрический ток в различных средах
Электрический ток в различных средах Метод координат (9 класс)
Метод координат (9 класс) PF_Kulon
PF_Kulon Применение закона рычага к блоку.
Применение закона рычага к блоку. Магнитное поле
Магнитное поле Аттестационная работа. Эссэ «Исследовательская работа учащихся на уроках физики»
Аттестационная работа. Эссэ «Исследовательская работа учащихся на уроках физики» Кристаллическое строение материалов
Кристаллическое строение материалов Гидроэлектростанции (ГЭС)
Гидроэлектростанции (ГЭС)  Основи теорії надійності
Основи теорії надійності Скорость света
Скорость света 1. Законы соединений. 2. Задачи.
1. Законы соединений. 2. Задачи. Научно-исследовательская работа «Холодильник в дорогу». Способ поддержания определенной температуры хранения вне холодильника
Научно-исследовательская работа «Холодильник в дорогу». Способ поддержания определенной температуры хранения вне холодильника Свойства пространства-времени и интегралы состояния: четность
Свойства пространства-времени и интегралы состояния: четность Взаимодействие в силе трения и силе упругости является электромагнитным
Взаимодействие в силе трения и силе упругости является электромагнитным Презентация по физике "Розвиток ядерної Енергетики в Україні" - скачать бесплатно
Презентация по физике "Розвиток ядерної Енергетики в Україні" - скачать бесплатно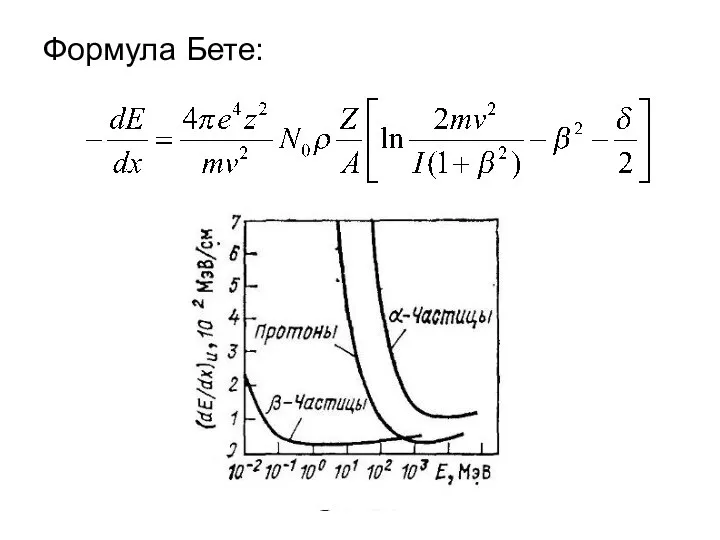 Формула Бете. (Лекция 4)
Формула Бете. (Лекция 4)