Содержание
- 2. Модели в механике. Система отсчета. Траектория, длина пути, вектор перемещения Простейшей формой движения является механическое движение.
- 3. Материальная точка, где же тебя разыскать? Можно любое взять тело: слона, бегемота, кровать. Только сравни для
- 4. При взаимодействии друг с другом тела могут деформироваться, т. е. изменять свою форму и размеры. В
- 5. Как ясно из определения механического движения, необходимо определить тело отсчета, то есть то тело, относительно которого
- 6. Длина траектории – путь, А траектория – линия. Ты это, дружок, не забудь. Взгляни-ка на небо
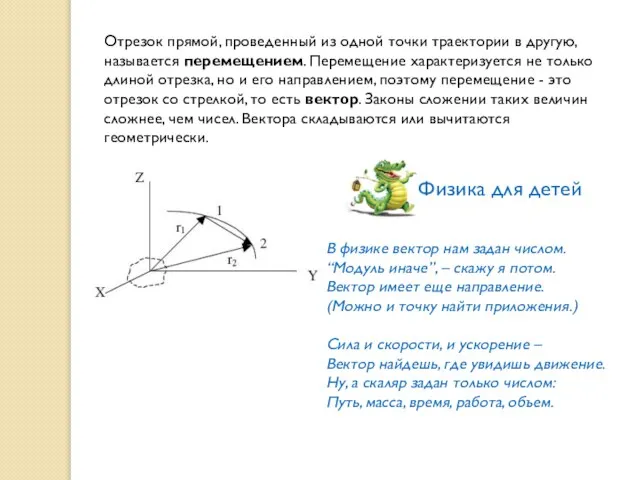
- 7. Отрезок прямой, проведенный из одной точки траектории в другую, называется перемещением. Перемещение характеризуется не только длиной
- 8. Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами.
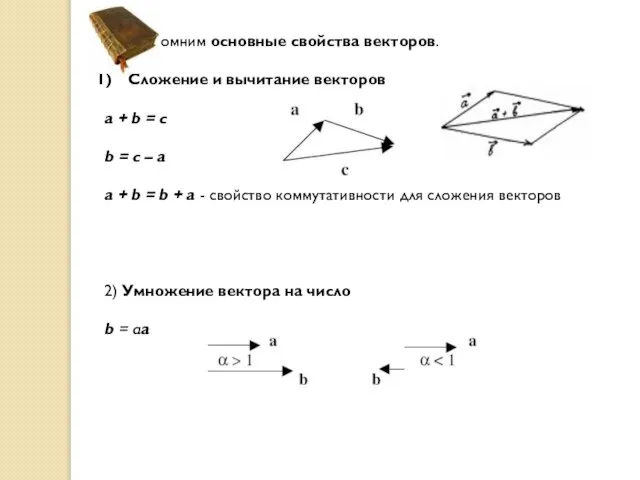
- 9. Вспомним основные свойства векторов. Сложение и вычитание векторов a + b = c b = c
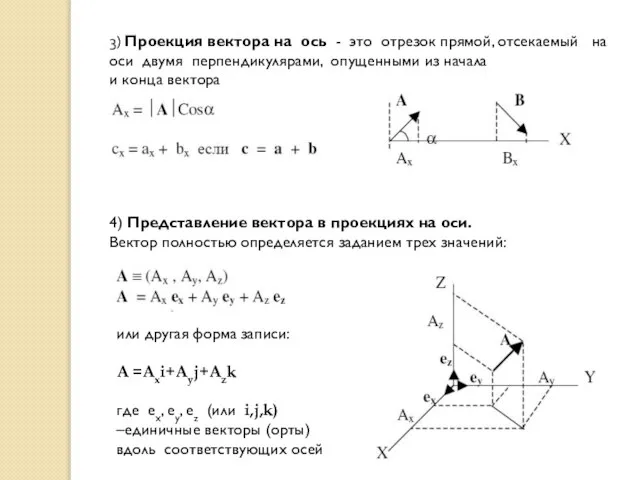
- 10. 3) Проекция вектора на ось - это отрезок прямой, отсекаемый на оси двумя перпендикулярами, опущенными из
- 11. 5) Скалярное произведение векторов. В результате получается скаляр. Свойства скалярного произведения коммутативность : ассоциативность : A
- 12. 7) Векторное произведение векторов А и В - это вектор, обозначаемый символом [AB] или A x
- 13. 9) Если даны две точки пространства A(a1 , a2 , a3) B(b1 , b2 , b3)
- 14. Задание. На оси Ox найти точку, равноудаленную от точек A(2;−4; 5) и B(−3; 2; 7). Решение.
- 15. Задание. Найти косинус угла между векторами AB и AC . Точки A,B,C заданы: A(−4; 4;4), B(3;1;0),
- 16. Движение материальной точки При движении материальной точки ее координаты с течением времени изменяются. В общем случае
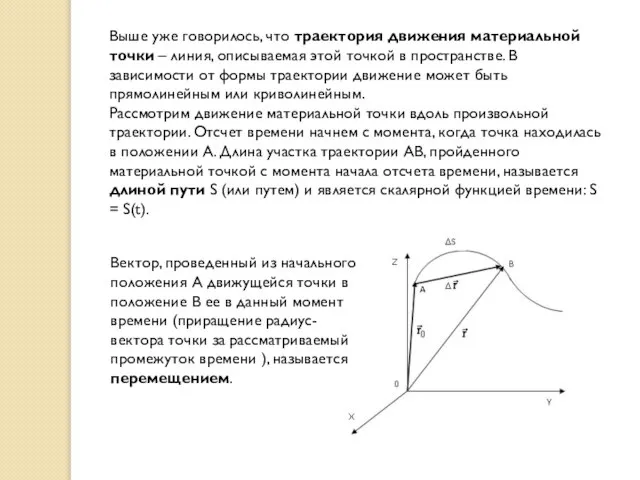
- 17. Выше уже говорилось, что траектория движения материальной точки – линия, описываемая этой точкой в пространстве. В
- 18. Не думай, что просто судить о движении – Здесь множество будет подводных камней. Туман на реке,
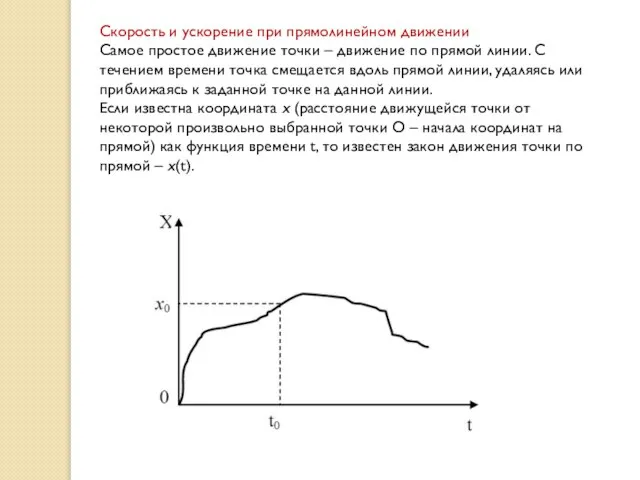
- 19. Скорость и ускорение при прямолинейном движении Самое простое движение точки – движение по прямой линии. С
- 20. Путь, пройденный точкой, можно определить по ее координате только в том случае, если точка движется в
- 21. Очевидно, что средняя скорость зависит от промежутка времени, за который мы ее определяем. Если средняя скорость
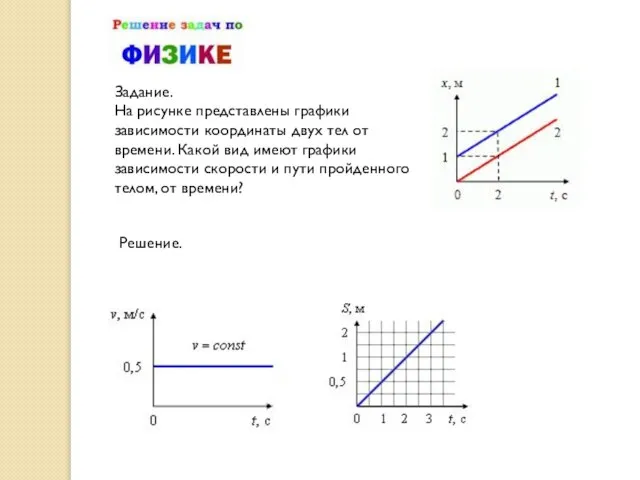
- 22. Задание. На рисунке представлены графики зависимости координаты двух тел от времени. Какой вид имеют графики зависимости
- 23. При неравномерном движении средняя скорость будет различной в зависимости от того, за какой промежуток времени мы
- 24. Расстояние, пройденное точкой за промежуток времени t2t1 при постоянной скорости v0, очевидно равно произведению скорости v0
- 25. Предположим, что мы разбили весь промежуток времени t2t1 на бесконечно большое число малых промежутков dt. Каждому
- 26. При неравномерном движении точка имеет переменную скорость, которую, подобно координате, можно рассматривать как функцию времени v(t).
- 27. Движение с постоянным ускорением называется равнопеременным. В этом случае зависимости координаты х и скорости v от
- 28. Задание. В 10:00 туристы на лодке поплыли из пункта А вниз по течению реки. Пройдя 12
- 29. Задание. Даны уравнения движения тела: x = vxt и y = yo + vyt. Запишите уравнение
- 30. Задание. Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду движется товарный поезд длиной
- 31. Задание. Буратино и Пьеро бежали наперегонки. Пьеро весь путь бежал с одной и той же скоростью,
- 32. Задание. Если Аня идёт в школу пешком, а обратно едет на автобусе, то всего на дорогу
- 33. Задание. Первую половину пути автомобиль проехал со скоростью v1 = 60 км/ч, а вторую — со
- 35. Скачать презентацию


























 Рідкі кристали та їх використання
Рідкі кристали та їх використання Кинематика вращательного движения. Поступательное движение твердого тела. Теорема о движении центра масс. Работа и энергия
Кинематика вращательного движения. Поступательное движение твердого тела. Теорема о движении центра масс. Работа и энергия Дифракция құбылысы. Френел және Фраунгофер жуықтаулары. Амплитудалық және фазалық дифракциялық торлар
Дифракция құбылысы. Френел және Фраунгофер жуықтаулары. Амплитудалық және фазалық дифракциялық торлар Нашему отделу – 30 лет. Планетные миссии с участием нашего отдела
Нашему отделу – 30 лет. Планетные миссии с участием нашего отдела Распространение волн
Распространение волн Матрица рассеяния. Согласующие устройства
Матрица рассеяния. Согласующие устройства Московский городской педагогический университет Педагогический институт физической культуры Кафедра информатизации образовани
Московский городской педагогический университет Педагогический институт физической культуры Кафедра информатизации образовани Механические колебания и их характеристики. Виды колебаний. Механические волны
Механические колебания и их характеристики. Виды колебаний. Механические волны Механические колебания
Механические колебания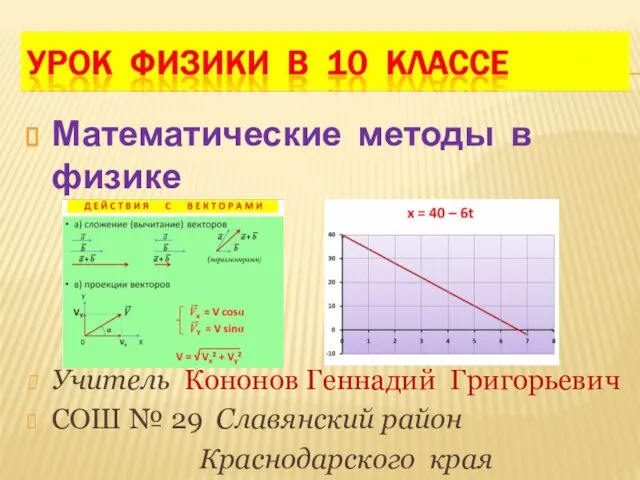 Математические методы в физике Математические методы в физике Учитель Кононов Геннадий Григорьевич СОШ № 29 Славянский ра
Математические методы в физике Математические методы в физике Учитель Кононов Геннадий Григорьевич СОШ № 29 Славянский ра Нанотехнологии
Нанотехнологии Гармоническое колебательное движение. (Лекция 6)
Гармоническое колебательное движение. (Лекция 6) Волноводы с волнами типа Т. Лекция 11
Волноводы с волнами типа Т. Лекция 11 Развитие ракетной техники
Развитие ракетной техники Кинематическое исследование механизмов и машин
Кинематическое исследование механизмов и машин Квантовая теория свободного поля излучения
Квантовая теория свободного поля излучения Презентация Механика Ньютона
Презентация Механика Ньютона Температуралық тепе-теңдік күйіндегі денелердің сәуле шығаруы. Қара дененің сәуле шығару заңдары. (Лекция 14)
Температуралық тепе-теңдік күйіндегі денелердің сәуле шығаруы. Қара дененің сәуле шығару заңдары. (Лекция 14) Оќыту процессінде композициялыќ жобалау єдісін ќолдану
Оќыту процессінде композициялыќ жобалау єдісін ќолдану Физика тапсырмалары
Физика тапсырмалары Проводниковые материалы. Контактные явления. (Лекция 3.2)
Проводниковые материалы. Контактные явления. (Лекция 3.2) «Световые явления» задания 8 класс Разработала: Аксёнова Наталья Петровна, МОУ «СОШ № 100» г. Новокузнецк 2010 г.
«Световые явления» задания 8 класс Разработала: Аксёнова Наталья Петровна, МОУ «СОШ № 100» г. Новокузнецк 2010 г.  Пляшущий мяч
Пляшущий мяч Классификация парогенераторов АЭС
Классификация парогенераторов АЭС Дальність дії радіолокатора
Дальність дії радіолокатора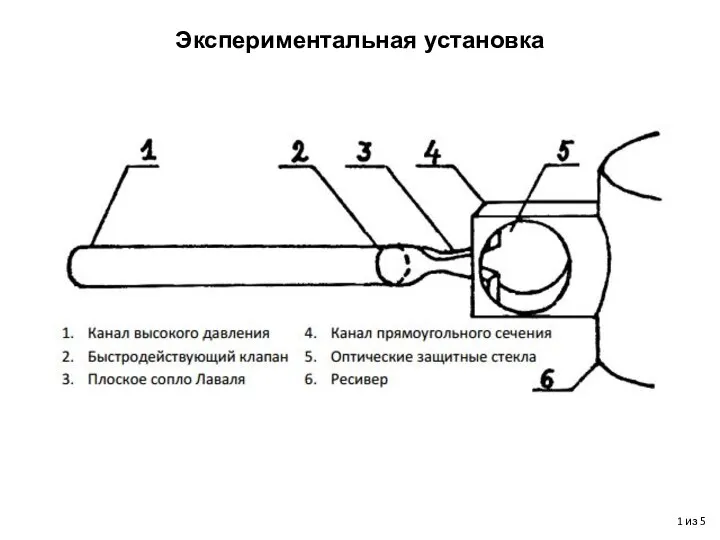 Экспериментальная установка. Метод интерферометра
Экспериментальная установка. Метод интерферометра Проводники в электрическом поле Проводники – это вещества,в которых много свободных заряженных частиц. Например в металлах эт
Проводники в электрическом поле Проводники – это вещества,в которых много свободных заряженных частиц. Например в металлах эт Механічний рух з урахуванням закону збереження енергії Вчитель: Роїк Леся Василівна Виконала: учениця 10-А класу Збаранська Со
Механічний рух з урахуванням закону збереження енергії Вчитель: Роїк Леся Василівна Виконала: учениця 10-А класу Збаранська Со