8-800-333-86-44
Клиентам
Авторам
Цены и срокиСпособы оплатыОтзывыО компанииКонтакты
Вход
Главная
Блог
Полезно знать
Система уравнений Максвелла для электромагнитного поля:
смысл, способы решения
Система уравнений Максвелла для электромагнитного поля: смысл, способы решения
Полезно знать Подготовка к экзамену Физика для "чайников"
Иван27 Июнь 201717 264
Нет времени писать работу?
Доверь это кандидату наук!
Узнай стоимость
Содержание
Содержание
Первое уравнение Максвелла
Третье уравнение Максвелла
Второе уравнение Максвелла
Четвертое уравнение Максвелла
Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.
Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.
Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.
Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.
Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.
Стационарное электрическое поле
Первое уравнение: электрический заряд порождает электрическое поле
Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле
Третье уравнение: магнитных зарядов не существует
Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле
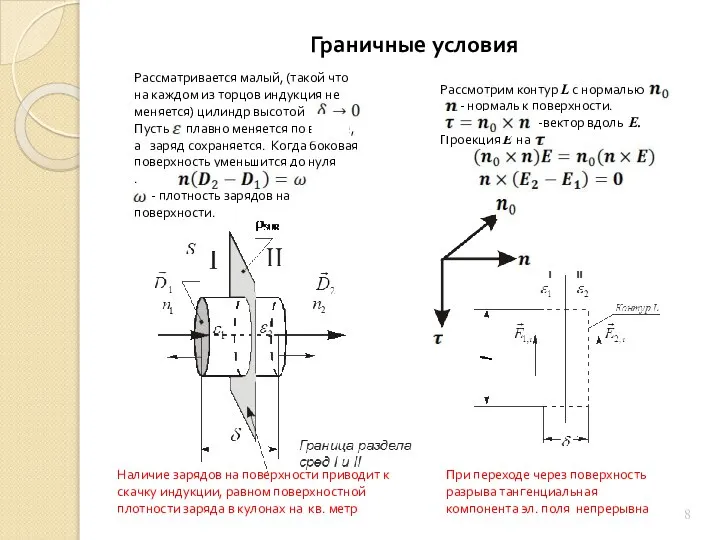
Уравнения Максвелла
Исключив зависимость от времени, получаем:
Из второго следует, что Е можно представить в виде
- скалярный потенциал
Минус выбран для того, чтобы выполнить общепринятое условие:
«вектор Е направлен от положительного заряда к отрицательному»




















 Электромагнитные излучения в жизни человека
Электромагнитные излучения в жизни человека Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний. Переменный ток
Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний. Переменный ток Презентація з фізичного практикуму на тему:”Фізика й науково-технічний прогрес” підготувала: учениця 11-А класу Харківської ЗОШ І-ІІІ ст №102 Антіпова Марія
Презентація з фізичного практикуму на тему:”Фізика й науково-технічний прогрес” підготувала: учениця 11-А класу Харківської ЗОШ І-ІІІ ст №102 Антіпова Марія  Горное давление
Горное давление Электрический ток в различных средах. Электрический ток в металлах
Электрический ток в различных средах. Электрический ток в металлах Колебания кристаллической решетки
Колебания кристаллической решетки ЛЕКЦИЯ 3. Динамика системы материальных точек. Работа и энергия
ЛЕКЦИЯ 3. Динамика системы материальных точек. Работа и энергия Механические колебания и волны. Уравнение плоской волны. Волновое уравнение. Звуковые волны. Ультразвук. Лекция 1
Механические колебания и волны. Уравнение плоской волны. Волновое уравнение. Звуковые волны. Ультразвук. Лекция 1 Значення атмосферного тиску в житті людей
Значення атмосферного тиску в житті людей Удивительные и странные свойства воды
Удивительные и странные свойства воды Геофизические исследования скважин
Геофизические исследования скважин Волновая оптика
Волновая оптика Магнитные явления в природе Выполнил: ученик 11 И класса МОУ СОШ №2 Мамедов Сабир Мирза оглы. Научный руководитель: Рыбалкина Св
Магнитные явления в природе Выполнил: ученик 11 И класса МОУ СОШ №2 Мамедов Сабир Мирза оглы. Научный руководитель: Рыбалкина Св Задачи по теме «Законы сохранения»
Задачи по теме «Законы сохранения» Задачи для самостоятельного решения
Задачи для самостоятельного решения Броуновское движение
Броуновское движение Кинематика. Механика
Кинематика. Механика Технические изобретения 17,18,19 и начало 20 века
Технические изобретения 17,18,19 и начало 20 века Вивчаємо броунівський рух разом з нами
Вивчаємо броунівський рух разом з нами Физика на кухне
Физика на кухне Виды самоходной техники в АПК:
Виды самоходной техники в АПК: Единицы измерения энергии
Единицы измерения энергии Презентация Магнитное поле Земли
Презентация Магнитное поле Земли  Эхо. Световое эхо
Эхо. Световое эхо Механические колебания
Механические колебания Экзотические и перспективные виды электростанций
Экзотические и перспективные виды электростанций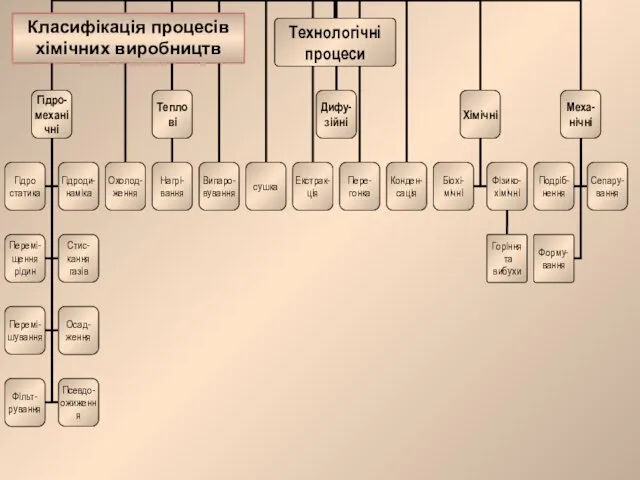 Класифікація процесів хімічних виробництв
Класифікація процесів хімічних виробництв Исследовательский проект по физике
Исследовательский проект по физике