Понятие о простых формах. Номенклатура простых форм высшей категории. Простые формы кристаллов высшей категории
Содержание
- 2. Практическое занятие 5. Понятие о простых формах Простой формой называется совокупность граней, связанных элементами симметрии. Грани
- 3. Практическое занятие 5. Понятие о простых формах Комбинацией называется совокупность двух или нескольких простых форм. Все
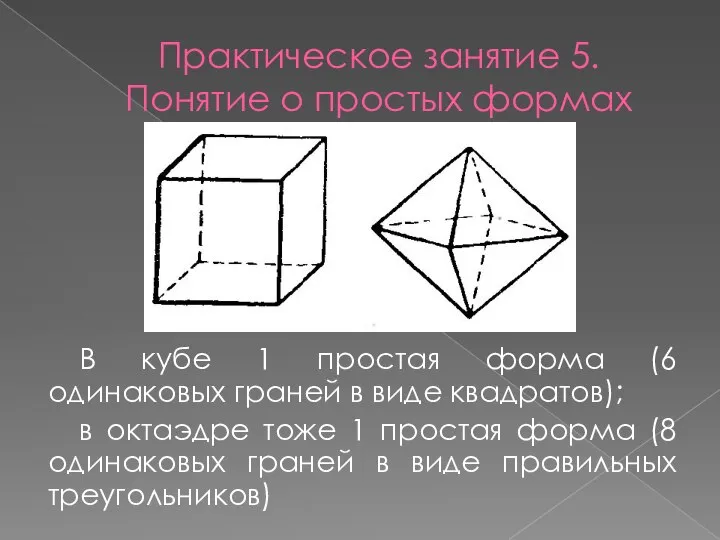
- 4. Практическое занятие 5. Понятие о простых формах В кубе 1 простая форма (6 одинаковых граней в
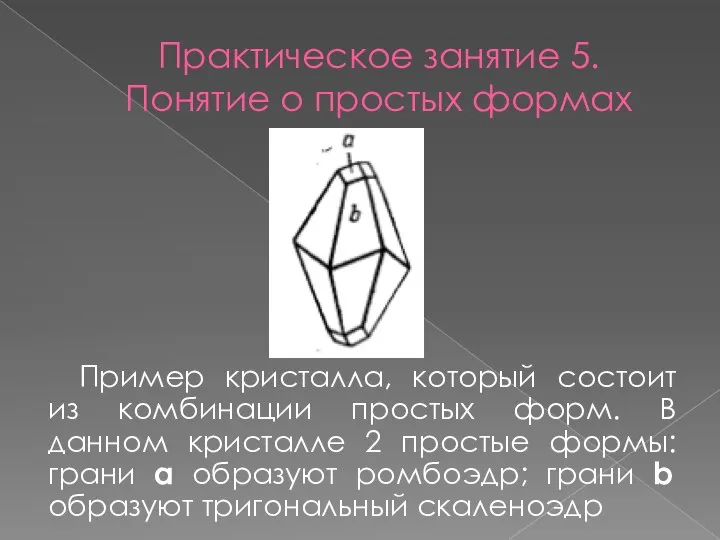
- 5. Практическое занятие 5. Понятие о простых формах Пример кристалла, который состоит из комбинации простых форм. В
- 6. Практическое занятие 5. Понятие о простых формах При подсчете простых форм в комбинации (на моделях идеальных
- 7. Практическое занятие 5. Номенклатура простых форм высшей категории Моно – один; ди – два; тетра –
- 8. Практическое занятие 5. Номенклатура простых форм высшей категории Тетраэдр – тетра (4) + эдр (грань) =
- 9. Практическое занятие 5. Простые формы кристаллов высшей категории В кристаллах кубической сингонии выделяют 15 простых форм.
- 10. Практическое занятие 5. Простые формы кристаллов высшей категории К таким исходным (простейшим) формам относятся: 1) тетраэдр
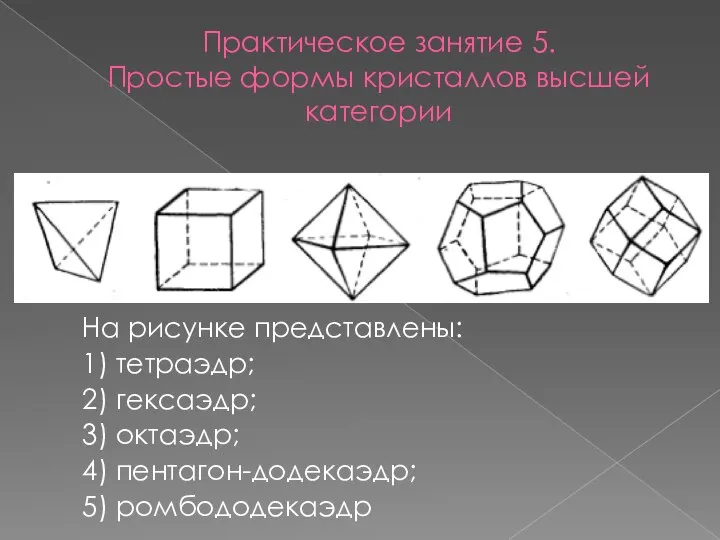
- 11. Практическое занятие 5. Простые формы кристаллов высшей категории На рисунке представлены: 1) тетраэдр; 2) гексаэдр; 3)
- 12. Практическое занятие 5. Простые формы кристаллов высшей категории Начнем с производных тетраэдра. Утроив его грани, получим
- 13. Практическое занятие 5. Простые формы кристаллов высшей категории Тригон-тритетраэдр – тригон (треугольник) + тритетраэдр (3*4=12 граней)
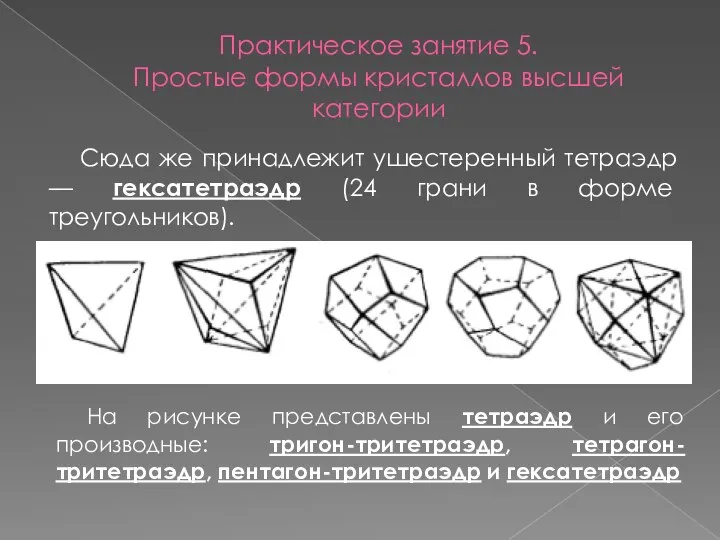
- 14. Практическое занятие 5. Простые формы кристаллов высшей категории Сюда же принадлежит ушестеренный тетраэдр — гексатетраэдр (24
- 15. Практическое занятие 5. Простые формы кристаллов высшей категории Октаэдр дает новую серию производных, аналогичную тетраэдрической. Утраивая
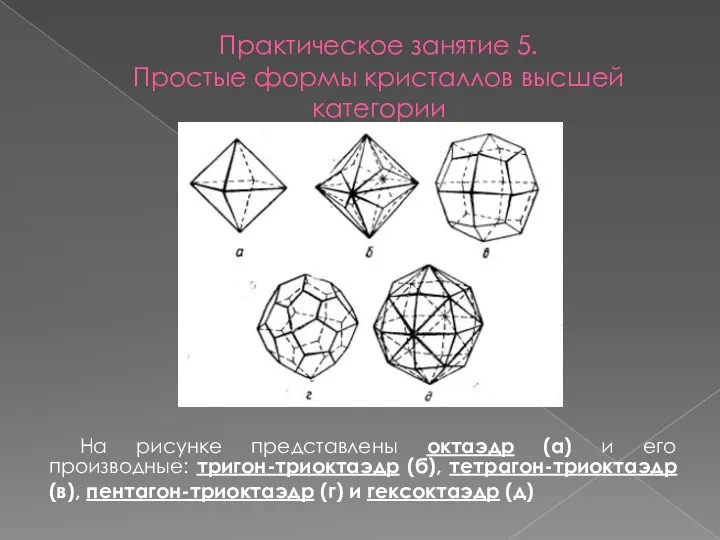
- 16. Практическое занятие 5. Простые формы кристаллов высшей категории На рисунке представлены октаэдр (а) и его производные:
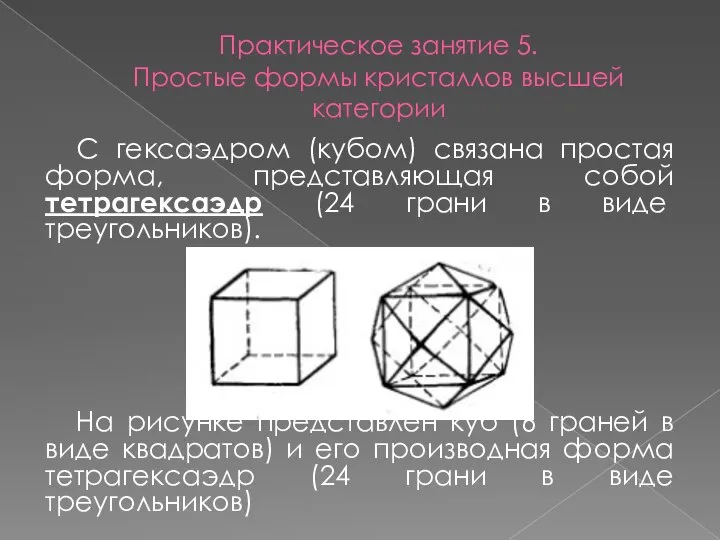
- 17. Практическое занятие 5. Простые формы кристаллов высшей категории С гексаэдром (кубом) связана простая форма, представляющая собой
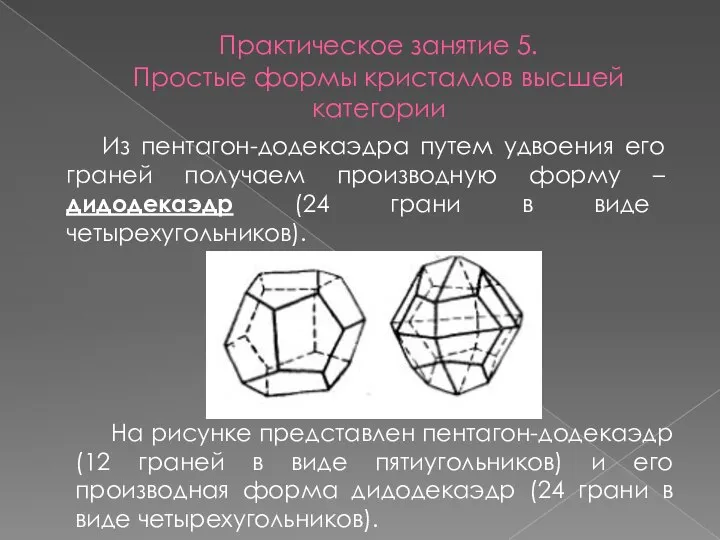
- 18. Практическое занятие 5. Простые формы кристаллов высшей категории Из пентагон-додекаэдра путем удвоения его граней получаем производную
- 19. Практическое занятие 5. Простые формы кристаллов высшей категории Ромбододекаэдр (12 граней в виде ромбов) представляет собой
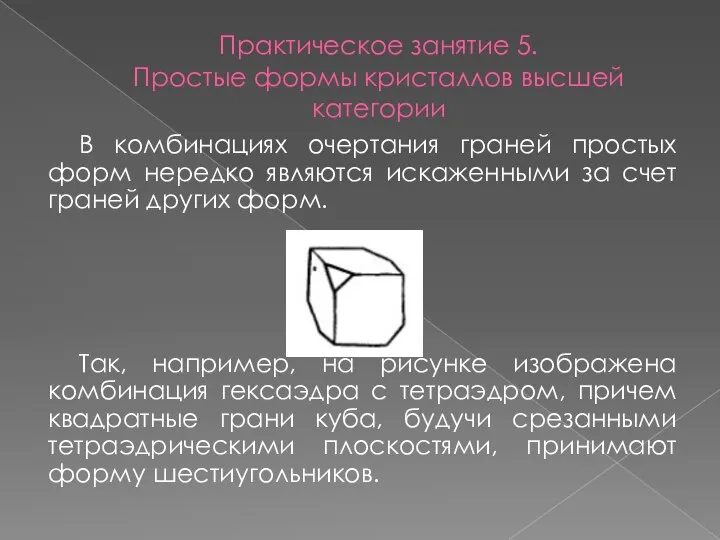
- 20. Практическое занятие 5. Простые формы кристаллов высшей категории В комбинациях очертания граней простых форм нередко являются
- 22. Скачать презентацию











 Топлива и их свойства. Топлива автомобилей
Топлива и их свойства. Топлива автомобилей Вода - растворитель
Вода - растворитель Щелочные металлы
Щелочные металлы Амфотерні гідроксиди
Амфотерні гідроксиди Личностно – ориентированный подход в обучении химии Талавир С.Е. Учитель химии МОУ СОШ№5
Личностно – ориентированный подход в обучении химии Талавир С.Е. Учитель химии МОУ СОШ№5 Химические реакции. Скорость реакции
Химические реакции. Скорость реакции Понятие о коррозии металлов. Способы защиты от коррозии
Понятие о коррозии металлов. Способы защиты от коррозии Соли в природе. Реакции с участием солей. Модуль 2. Лекция 2.1
Соли в природе. Реакции с участием солей. Модуль 2. Лекция 2.1 Centrifugal Ultrafiltration Devices
Centrifugal Ultrafiltration Devices Ацетилен
Ацетилен Производные углеводородов с одновалентной функцией
Производные углеводородов с одновалентной функцией Свойства моторных топлив
Свойства моторных топлив Безопасная помада
Безопасная помада Вода - чудо, сотворенное природой
Вода - чудо, сотворенное природой Именные реакции в органической химии
Именные реакции в органической химии Физические явления - основа разделения смесей в химии
Физические явления - основа разделения смесей в химии Алкилирование изобутана олефинами
Алкилирование изобутана олефинами Алкины. Свойства, получение и применение
Алкины. Свойства, получение и применение Основные этапы развития химии комплексных соединений Лектор: канд. хим. наук, ст. преп. Камиль Абрарович Сагдеев
Основные этапы развития химии комплексных соединений Лектор: канд. хим. наук, ст. преп. Камиль Абрарович Сагдеев Аренкарбонільні комплекси металів у реакціях перфлюороалкілювання та деароматизації
Аренкарбонільні комплекси металів у реакціях перфлюороалкілювання та деароматизації Роль хімії у житті суспільства.
Роль хімії у житті суспільства.  Хімічні методи підвищення продуктивності свердловини
Хімічні методи підвищення продуктивності свердловини Выделение урана из растворов (пульп)
Выделение урана из растворов (пульп) Ионное произведение воды. Понятие о рН раствора
Ионное произведение воды. Понятие о рН раствора Теоретическое и прикладное материаловедение
Теоретическое и прикладное материаловедение Атомы и молекулы. Простые и сложные вещества. 8 класс
Атомы и молекулы. Простые и сложные вещества. 8 класс Нанокомпозиционный материал на основе фенолоформальдегидной смолы, эпоксидной смолы, полистирола
Нанокомпозиционный материал на основе фенолоформальдегидной смолы, эпоксидной смолы, полистирола Важнейшие классы неорганических соединений Школа № 279 г. Санкт-Петербург Е. В Переверзева
Важнейшие классы неорганических соединений Школа № 279 г. Санкт-Петербург Е. В Переверзева