Содержание
- 2. לוגיקה במדעי המחשב מחשב מחקה יכולת שכלית (היגיון) תוכנית מחשב – סוג של הוכחה. תורת התכנות-
- 3. טיעונים אם רכבת מאחרת וגם אין מוניות זמינות בתחנה, אז אלי מאחר לפגישה. אבל אלי לא
- 4. נדון בפסוקיי חיווי, אשר יש להם בדיוק אחד משני ערכים: אמת (True) או שקר (False). 1.
- 5. קשרים לוגיים שלילה (negation) ¬P : "לא P". קוניונקציה (conjunction, גימום) P∧Q: "P ו- Q“. דיסיונקציה
- 6. תחביר הגדרה: נוסחא נקראת בנויה היטב (well-formed formula) אם ניתן ליצור אותה לפי החוקים הבאים: כל
- 7. פסוקים מורכבים דוגמא: ,(p∨q) ,((p∧q)∨(¬p)) ,((¬p)∨q) ¬(¬p))) ולא ((p ∧ q)), (p ∧ q ∧ r),
- 8. אינדוקציה על נוסחאות אם תכונה P נכונה לכל הפסוקים האטומיים, ומהנחה ש-P נכונה לנוסחאות A ו-B
- 9. הצרנה זהו מקס או שההוא מוריץ ואני ליצן: p ∨ q ∧ r אני אגיע הביתה
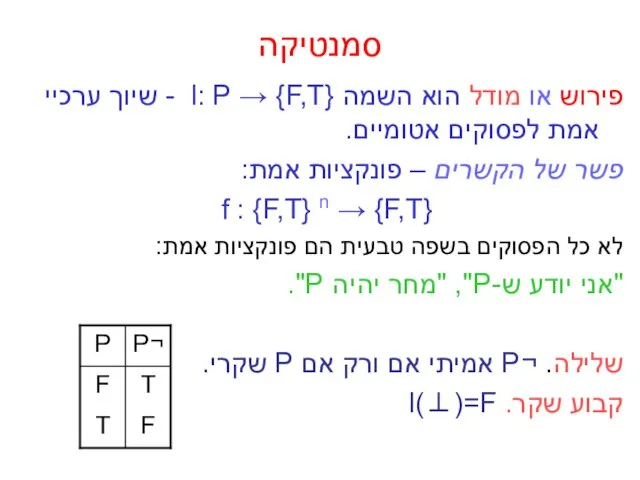
- 10. סמנטיקה פירוש או מודל הוא השמה l: P → {F,T} - שיוך ערכיי אמת לפסוקים אטומיים.
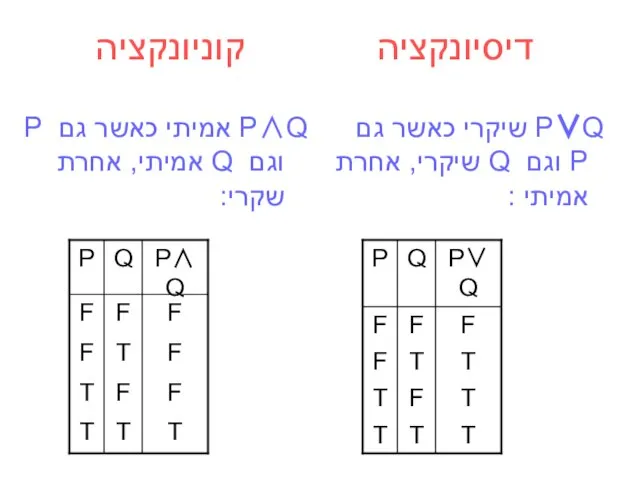
- 11. דיסיונקציה קוניונקציה P∧Q אמיתי כאשר גם P וגם Q אמיתי, אחרת שקרי: P∨Q שיקרי כאשר גם
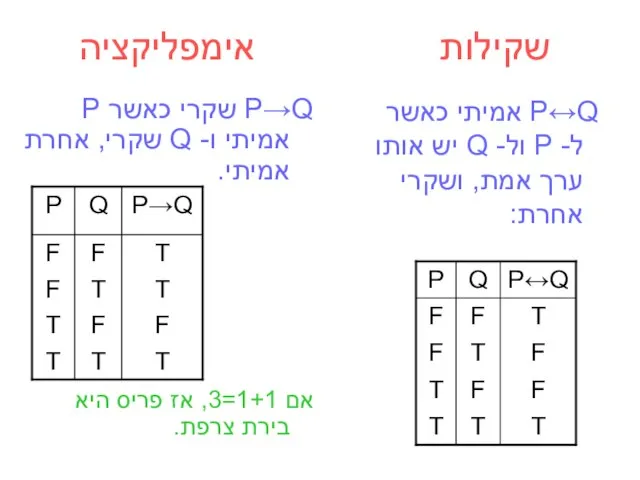
- 12. שקילות אימפליקציה P→Q שקרי כאשר P אמיתי ו- Q שקרי, אחרת אמיתי. אם 1+1=3, אז פריס
- 13. יחס ספיקות הגדרה. (הרחבה של פירוש לפסוקים מורכבים) l(⊥)=F l(¬A)=T אם ורק אם l(A)=F l(A∧B)=T אם
- 14. בעיות ספיקות ותקפות נוסחה נקראת ספיקה (או עקבית) אם יש לה מודל. נוסחה לא ספיקה נקראת
- 15. טבלאות אמת טבלת אמת של פסוק מורכב מתארת את ערכי האמת של הפסוק עבור כל פרוש.
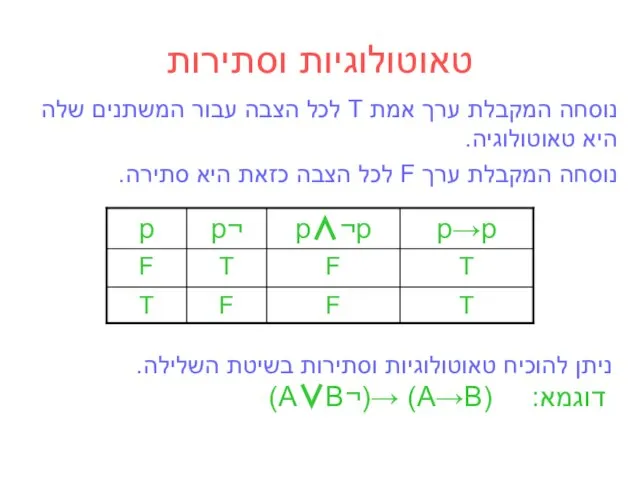
- 16. טאוטולוגיות וסתירות נוסחה המקבלת ערך אמת T לכל הצבה עבור המשתנים שלה היא טאוטולוגיה. נוסחה המקבלת
- 17. שקילות של פסוקים שני פסוקים נקראים שקולים אם יש להם אותם מודלים. פסוקים שקולים מהבאים אותה
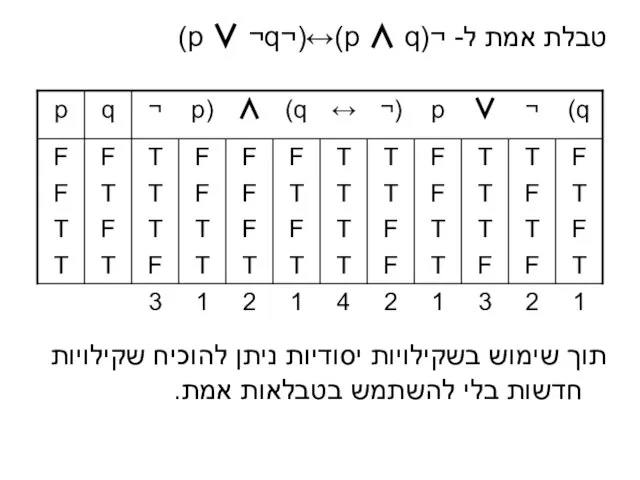
- 18. טבלת אמת ל- ¬(p ∧ q)↔(¬p ∨ ¬q) תוך שימוש בשקילויות יסודיות ניתן להוכיח שקילויות חדשות
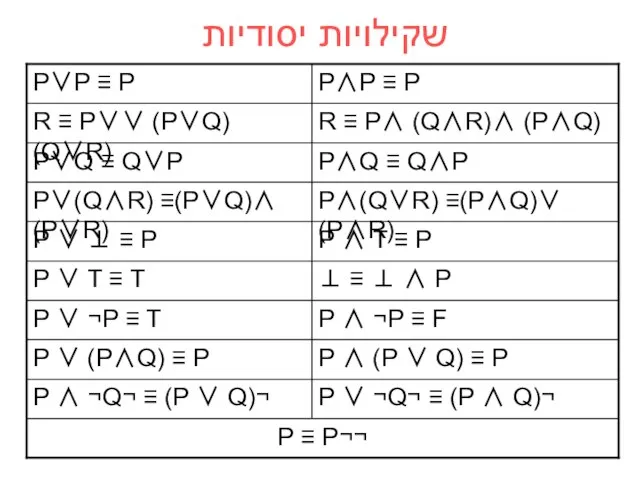
- 19. שקילויות יסודיות
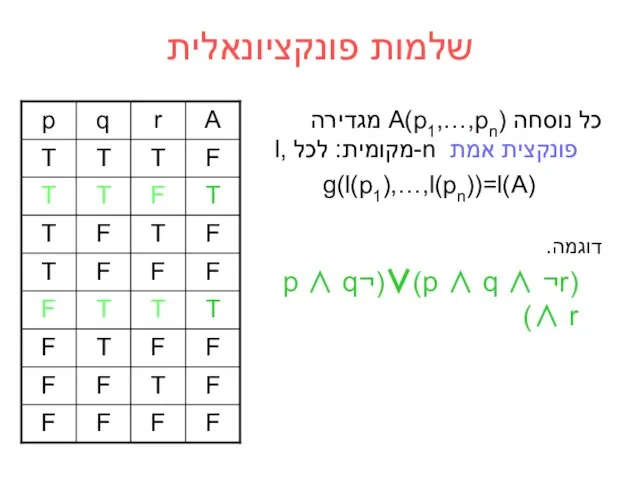
- 20. שלמות פונקציונאלית כל נוסחה A(p1,…,pn) מגדירה פונקצית אמת n-מקומית: לכל ,l g(l(p1),…,l(pn))=l(A) דוגמה. (p ∧ q
- 21. משפת (שלמות פונקציונאלית). לכל פונקצית אמת קיימת נוסחה המגדירה אותה. הוכחה. תהיה f פונקצית אמת n-מקומית.
- 22. קבוצות שלמות של קשרים הגדרה: קבוצה של קשרים שבאמצעותם ניתן לתאר כל פונקצית אמת נקראת קבוצה
- 23. קבוצות לא שלמות של קשרים למה. {↔,∨,∧, →} היא קבוצה לא שלמה של קשרים. הוכחה. להבדיל
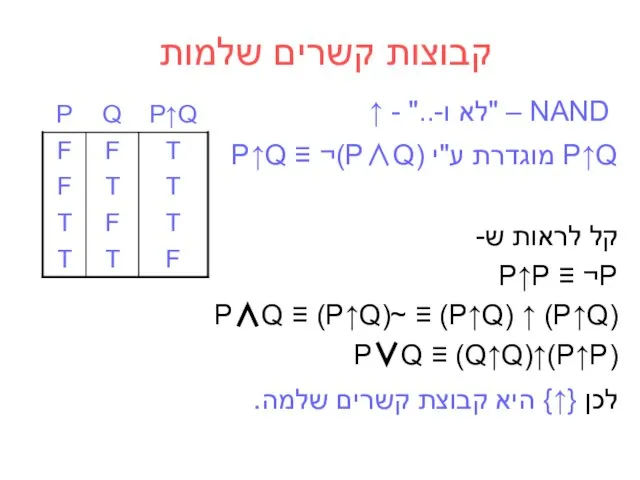
- 24. קבוצות קשרים שלמות NAND – "לא ו-.." - ↑ P↑Q מוגדרת ע"י P↑Q ≡ ¬(P∧Q) קל
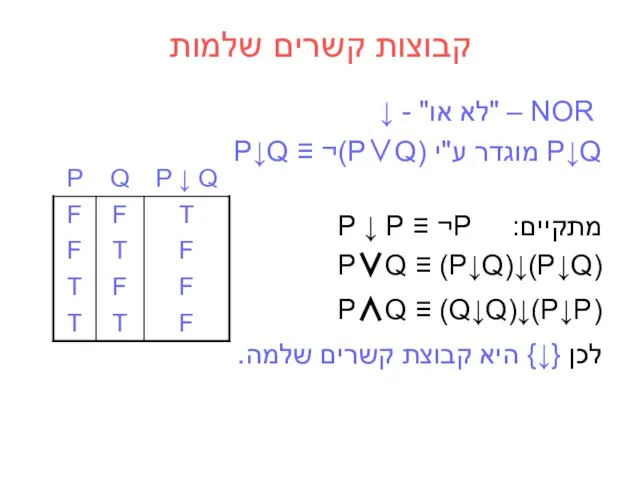
- 25. NOR – "לא או" - ↓ P↓Q מוגדר ע"י P↓Q ≡ ¬(P∨Q) מתקיים: P ↓ P
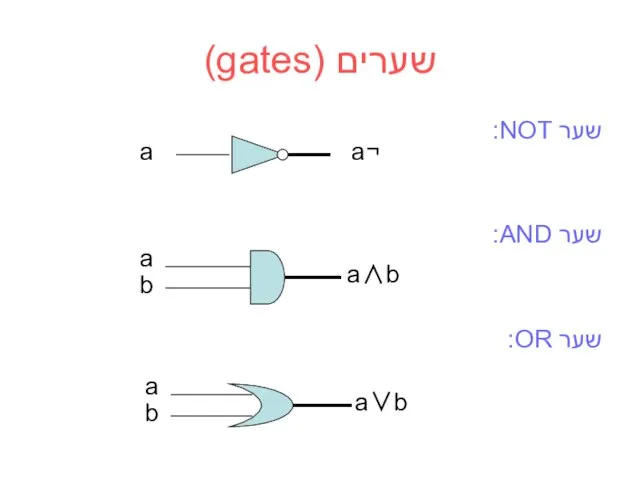
- 26. שערים (gates) שער NOT: שער AND: שער OR:
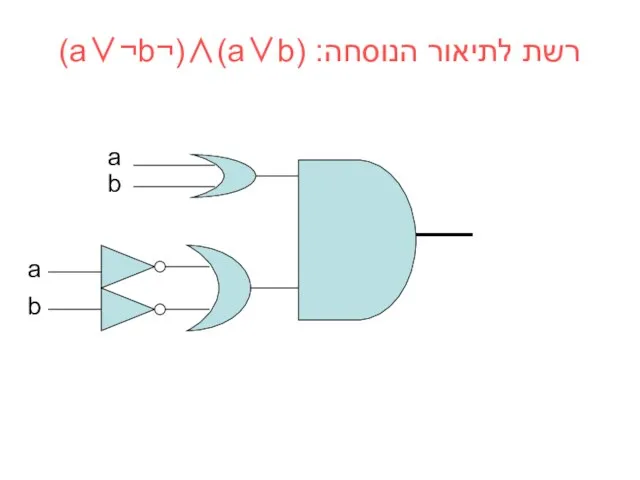
- 27. רשת לתיאור הנוסחה: (a∨b)∧(¬a∨¬b)
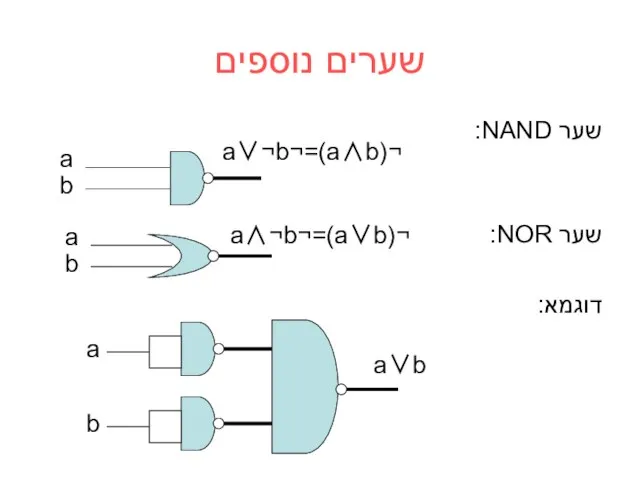
- 28. שערים נוספים שער NAND: שער NOR: דוגמא: a b a∨b
- 29. צורות נורמאליות אם p הוא פסוק אטומי, אז p ו-¬p הם ליטרלים. הגדרה. נוסחה בצורה דיסיונקטיבית
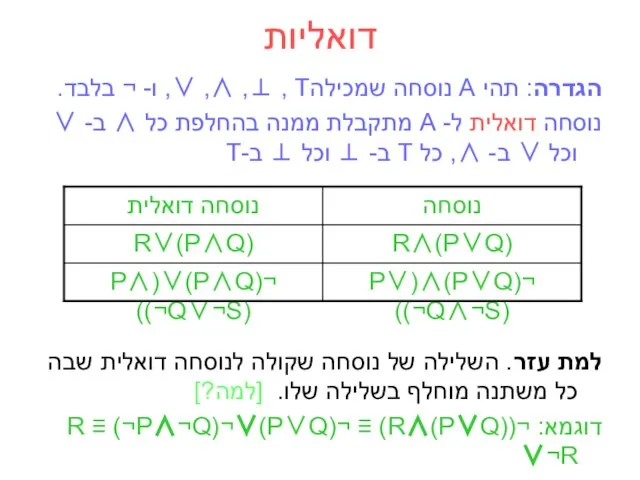
- 30. דואליות הגדרה: תהי A נוסחה שמכילהT , ⊥, ∧, ∨, ו- ¬ בלבד. נוסחה דואלית ל-
- 31. צורות נורמליות - המשך פסוקית (clause) היא דיסיונקציה של ליטרלים: r∨¬q∨¬p הגדרה. נוסחה בצורה קוניונקטיבית נורמאלית
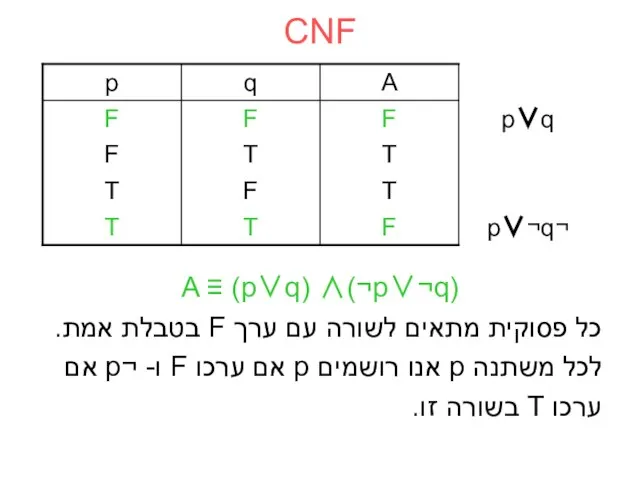
- 32. CNF A ≡ (p∨q) ∧(¬p∨¬q) כל פסוקית מתאים לשורה עם ערך F בטבלת אמת. לכל משתנה
- 33. אלגוריתמים לבניית DNF ו-CNF סילוק → ו- ;↔ הכנסת שלילה פנימה (צורת (NNF פריסה של ∨
- 34. פסוקיות הורן פסוקית הורן (Horn clause) היא פסוקית שמכילה לא יותר מליטרל חיובי אחד. p∨¬q1∨...∨¬qn (
- 35. אלגוריתם הכרעה לנוסחאות הורן אלגוריתם HORN להכרעת ספיקות: נסמן אטומים בנוסחת הורן לפי כללים הבאים: נסמן
- 37. Скачать презентацию




















 Администрирование информационных систем Администрирование БД. Автоматизация административных задач
Администрирование информационных систем Администрирование БД. Автоматизация административных задач  Analysis and Design of Data Systems. Relational Algebra 2 (Lecture 18)
Analysis and Design of Data Systems. Relational Algebra 2 (Lecture 18) Автор: Гортунова Надежда 1 курс начальное образование
Автор: Гортунова Надежда 1 курс начальное образование Презентация "СТРУКТУРЫ ДАННЫХ ТАБЛИЦЫ" - скачать презентации по Информатике
Презентация "СТРУКТУРЫ ДАННЫХ ТАБЛИЦЫ" - скачать презентации по Информатике Дополнительные возможности при работе с пользовательскими функциями
Дополнительные возможности при работе с пользовательскими функциями Тренировка ADC-C
Тренировка ADC-C Отчет по производственной практике п.м 01 Ввод и обработка цифровой информации
Отчет по производственной практике п.м 01 Ввод и обработка цифровой информации Моделирование в среде графического редактора
Моделирование в среде графического редактора Сервис хранения и обмена файлами
Сервис хранения и обмена файлами Модернизация ИТ-инфраструктуры с помощью Windows Server 2016 (совместно с Veeam Software)
Модернизация ИТ-инфраструктуры с помощью Windows Server 2016 (совместно с Veeam Software) Графический интерфейс ОС и приложений.
Графический интерфейс ОС и приложений. Редактирование текста. Работа с фрагментами
Редактирование текста. Работа с фрагментами Простые и составные операторы Если ветвь условной конструкции или тело цикла содержит несколько операторов, то они объединяются в составной оператор при помощи “{“ и “}”. Begin в Паскале соответствует “{“ в Си, End - “}”.
Простые и составные операторы Если ветвь условной конструкции или тело цикла содержит несколько операторов, то они объединяются в составной оператор при помощи “{“ и “}”. Begin в Паскале соответствует “{“ в Си, End - “}”. Измерение информации
Измерение информации Презентация "Объектно-ориентированная платформа Windows" - скачать презентации по Информатике
Презентация "Объектно-ориентированная платформа Windows" - скачать презентации по Информатике Язык SQL
Язык SQL Дети в ИНТЕРНЕТЕ
Дети в ИНТЕРНЕТЕ 2 Лекция 4_СистемыСчисления
2 Лекция 4_СистемыСчисления Презентация по информатике
Презентация по информатике Sourcing strategy - Telecom
Sourcing strategy - Telecom Получение государственных услуг в электронном виде, или Как стать на ты с порталом госуслуг
Получение государственных услуг в электронном виде, или Как стать на ты с порталом госуслуг Виды информационных измерительных систем. Каналы связи и интерфейсы ИИС
Виды информационных измерительных систем. Каналы связи и интерфейсы ИИС Обобщающий урок по теме: «ИНФОРМАЦИЯ » Цель урока: ОБОБЩИТЬ И СИСТЕМАТИЗИРОВАТЬ ЗНАНИЯ И УМЕНИЯ ПО ТЕМЕ «ИНФОРМАЦИЯ»
Обобщающий урок по теме: «ИНФОРМАЦИЯ » Цель урока: ОБОБЩИТЬ И СИСТЕМАТИЗИРОВАТЬ ЗНАНИЯ И УМЕНИЯ ПО ТЕМЕ «ИНФОРМАЦИЯ»  Общие сведения о языке программирования Паскаль
Общие сведения о языке программирования Паскаль Регистрация на сайте ГТО
Регистрация на сайте ГТО Устройства персонального компьютера
Устройства персонального компьютера Презентация "Электронные ресурсы для школы" - скачать презентации по Информатике
Презентация "Электронные ресурсы для школы" - скачать презентации по Информатике Цикл “for” на языке Паскаль
Цикл “for” на языке Паскаль