Содержание
- 2. 20 Error .90 .17 1 .76 1.0 0.0 1 4.5 -5.2 -2.0 -4.6 -1.5 3.7 2.9
- 3. 21 Key Concepts Gradient descent error is a function of the weights we want to reduce
- 4. 22 Gradient Descent λ error(λ) gradient = 1 current λ optimal λ
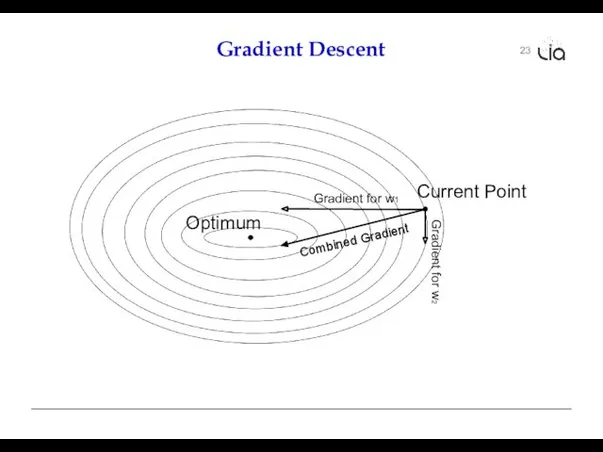
- 5. 23 Gradient Descent Gradient for w1 Gradient for w2 Optimum Current Point Combined Gradient
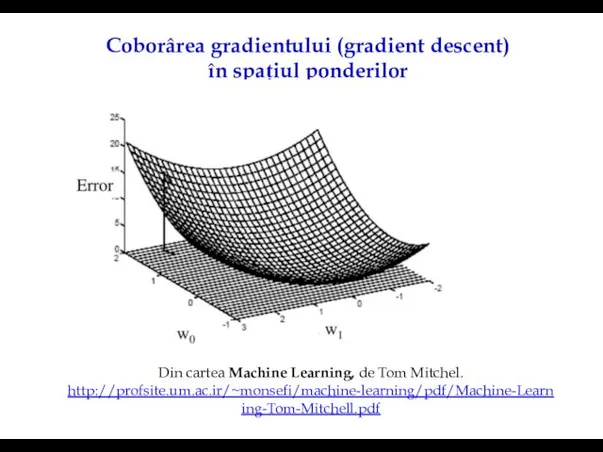
- 6. Coborârea gradientului (gradient descent) în spațiul ponderilor Din cartea Machine Learning, de Tom Mitchel. http://profsite.um.ac.ir/~monsefi/machine-learning/pdf/Machine-Learning-Tom-Mitchell.pdf
- 7. 24 Derivative of Sigmoid Sigmoid 1 sigmoid(x) = 1 + e−x Reminder: quotient rule Derivative dx
- 8. 25 Final Layer Update Linear combination of weights Activation function y = sigmoid(s) 2 Error (L2
- 9. 26 Final Layer Update (1) 2 Error (L2 norm) E = (t − y) 1 2
- 10. 27 Final Layer Update (2) Linear combination of weights Activation function y = sigmoid(s) 2 Error
- 11. 28 Final Layer Update (3) Linear combination of weights s = Σk wkhk Activation function y
- 12. 29 Putting it All Together Derivative of error with regard to one weight wk = dE
- 13. 30 Multiple Output Nodes Our example only had one output node Typically neural networks have multiple
- 14. 31 Hidden Layer Update In a hidden layer, we do not have a target output value
- 15. 32 Our Example .17 4.5 -5.2 -2.0 -4.6 -1.5 2.9 3.7 2.9 A 1.0 B 0.0
- 16. 33 Our Example .17 -4.6 -1.5 2.9 3.7 2.9 A 1.0 B 0.0 C 1 3.7
- 17. 34 Hidden Layer Updates .17 -4.6 -1.5 2.9 3.7 2.9 A 1.0 B 0.0 C 1
- 18. 35 some additional aspects
- 19. 36 Initialization of Weights Weights are initialized randomly e.g., uniformly from interval [−0.01, 0.01] Glorot and
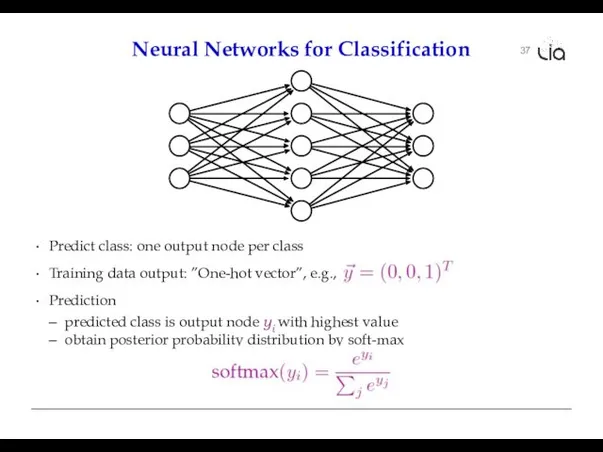
- 20. 37 Neural Networks for Classification Predict class: one output node per class Training data output: ”One-hot
- 21. 38 Problems with Gradient Descent Training error(λ) λ Too high learning rate
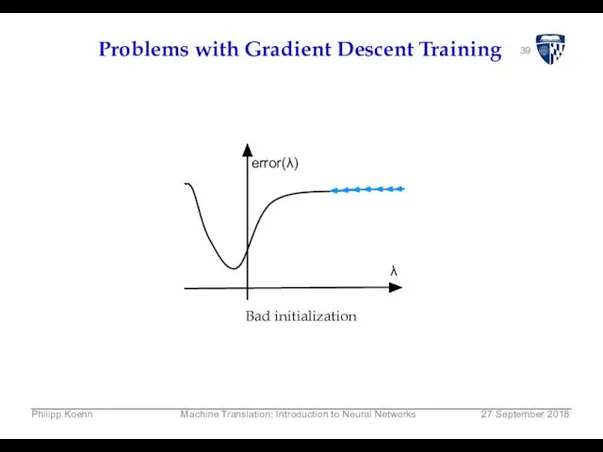
- 22. 39 Problems with Gradient Descent Training error(λ) λ Bad initialization Philipp Koehn Machine Translation: Introduction to
- 23. 40 Problems with Gradient Descent Training λ error(λ) local optimum global optimum Local optimum
- 24. 41 Speedup: Momentum Term Updates may move a weight slowly in one direction To speed this
- 25. 42 Adagrad Typically reduce the learning rate µ over time at the beginning, things have to
- 26. 43 Dropout A general problem of machine learning: overfitting to training data (very good on train,
- 27. 44 Mini Batches Each training example yields a set of weight updates ∆wi. Batch up several
- 28. 45 computational aspects
- 29. 46 Vector and Matrix Multiplications Forward computation: Activation function: Error term: Propagation of error term: Weight
- 30. 47 GPU Neural network layers may have, say, 200 nodes Computations such as require 200 ×
- 31. 48 Toolkits Theano Tensorflow (Google) PyTorch (Facebook) MXNet (Amazon) DyNet С (easy api)
- 32. lia@math.md
- 34. Скачать презентацию



























 Создание слайд-шоу. Фотоальбом. Урок 29
Создание слайд-шоу. Фотоальбом. Урок 29 SQL запросы
SQL запросы Лекция 12. Двусторонняя очередь: deque. Адаптеры контейнеров: stack, queue, priority_queue. Создание DLL
Лекция 12. Двусторонняя очередь: deque. Адаптеры контейнеров: stack, queue, priority_queue. Создание DLL Действия с информацией
Действия с информацией Проектирование Баз Данных. Основные понятия Теории Нормализации
Проектирование Баз Данных. Основные понятия Теории Нормализации Презентация к уроку информатики по теме «Растровое кодирование графической информации» Автор: Смелова Наталья Александровна, уч
Презентация к уроку информатики по теме «Растровое кодирование графической информации» Автор: Смелова Наталья Александровна, уч Что умеет компьютер
Что умеет компьютер Использование систем проверки орфографии и грамматики
Использование систем проверки орфографии и грамматики Нормальные формы баз данных
Нормальные формы баз данных Графический дизайн. Компьютерная графика
Графический дизайн. Компьютерная графика Метод координат
Метод координат Общая концепция. Поиск по всей базе данных
Общая концепция. Поиск по всей базе данных Требования к специалистам строительных организаций. Национальный реестр специалистов строительной отрасли
Требования к специалистам строительных организаций. Национальный реестр специалистов строительной отрасли Алгоритм с ветвлением
Алгоритм с ветвлением Инфологическая модель БД
Инфологическая модель БД Лекция № 15. Поиск и индексация
Лекция № 15. Поиск и индексация Использование график, таблиц, диаграмм в презентации. Лабораторная работа № 3
Использование график, таблиц, диаграмм в презентации. Лабораторная работа № 3 Архитектура компьютера Презентацию выполнила студентка 1 курса Ермакова Ольга
Архитектура компьютера Презентацию выполнила студентка 1 курса Ермакова Ольга Экспертные системы
Экспертные системы Создание документов на базе комплекса программных средств электронного офиса Microsoft Office
Создание документов на базе комплекса программных средств электронного офиса Microsoft Office Язык С# как современная альтернатива Паскалю и С++ для обучения основам алгоритмизации и программирования Павловская Татьяна А
Язык С# как современная альтернатива Паскалю и С++ для обучения основам алгоритмизации и программирования Павловская Татьяна А Тезисы. Доклад. Презентация. Всё о конференциях
Тезисы. Доклад. Презентация. Всё о конференциях Строки в языке программирования C++
Строки в языке программирования C++ Мобильная медиашкола
Мобильная медиашкола Как устроен компьютер
Как устроен компьютер Лексические основы, арифметические типы данных, переменные и константы, операторы, линейный алгоритм. (Семинар 1)
Лексические основы, арифметические типы данных, переменные и константы, операторы, линейный алгоритм. (Семинар 1) Обобщения
Обобщения Аттестационная работа. Творческие проекты в среде программирования скретч, для 5-6 класса
Аттестационная работа. Творческие проекты в среде программирования скретч, для 5-6 класса