Элементы компьютерной математики. (Лекция 7)

Содержание

Слайд 2

Тема: Элементы компьютерной математики (ЭКМ) III. Элементы машинной арифметики Коды для

Тема: Элементы компьютерной математики (ЭКМ)

III. Элементы машинной арифметики
Коды для представления

чисел со знаком
Формы представления чисел
Диапазон и точность представления чисел
Сложение и вычитание чисел с фиксированной запятой
Умножение и деление чисел с фиксированной запятой
Десятичные операции

Лекция №7

Слайд 3

Коды для представления чисел со знаком Чисел без знака (ЧБЗ), конечно,

Коды для представления чисел со знаком

Чисел без знака (ЧБЗ), конечно, недостаточно

для обеспечения вычислительных работ. Естественное же представление знаков «+» и «-» годится только для ввода-вывода.
Например, можно записать:
- 45 = - 558 = - 1011012 и т.п.
При вычислениях знак числа кодируют. Обычно так: код знака «плюс» - это 0, знак «минус» - 1.
Слайд 4

Коды для представления чисел со знаком Для представления чисел со знаком

Коды для представления чисел со знаком

Для представления чисел со знаком принято

использовать три таких специальных кода:
- прямой код;
- обратный код;
- дополнительный код.
Слайд 5

Коды для представления чисел со знаком Проще всего записываются числа в

Коды для представления чисел со знаком

Проще всего записываются числа в прямом

коде:
(45)пр = 0.45 = 0.558 =0.1011012,
(– 45)пр = 1.45 = 1,558 = 1.1011012,
(– 45,5)пр = 1.45,5 = 1.55,48 = 1.101101,12.
Точка «.» в записи прямою кода отделяет знаковый разряд от цифровых разрядов.
Слайд 6

Коды для представления чисел со знаком Правило получения прямого кода: цифровые

Коды для представления чисел со знаком

Правило получения прямого кода: цифровые разряды

числа не изменяются, знаковый разряд отделяемся от них точкой.
!!!, для положительных чисел все три кода совпадают. Поэтому формируем правило получения обрат­ного кода для отрицательных чисел: цифровые разряды двоичного числа инвертируются.
Слайд 7

Коды для представления чисел со знаком Примеры. (– 45)обр = (–

Коды для представления чисел со знаком

Примеры.
(– 45)обр = (– 1011012)обр =

1.0100102,
(– 45,5)обр = (– 101101,12)обр = 1.010010,02.
Если система не двоичная (q ≠ 2), действует общее правило: каждая цифра дополняется до значения (q – 1).
Слайд 8

Коды для представления чисел со знаком Примеры. (– 45)обр = 1.54

Коды для представления чисел со знаком

Примеры.
(– 45)обр = 1.54 = 1.228
(–

45,5)обр = 1.54,4обр = 1.22.38
Нуль в прямом и обратном кодах имеет двоякое представление:
(+ 0)пр = 0.0 … 0,
(– 0)пр = 1.0 ... 0,
(+ 0)обр = 0.0 … 0,
(– 0)обр = 1.1 ... 12 = 1.9 … 9 = ...
Дополнительный код отрицательного числа может быть получен прямо или косвенно (через обратный код).
Слайд 9

Коды для представления чисел со знаком Прямое правило: цифровые разряды отрицательного

Коды для представления чисел со знаком

Прямое правило:
цифровые разряды отрицательного числа

инвертируются, за исключением самой правой единицы и, возможно, стоящих за ней нулей (эта единица и нули не изменяются).
Слайд 10

Коды для представления чисел со знаком Примеры. (– 45)доп = (–

Коды для представления чисел со знаком

Примеры.
(– 45)доп = (– 1011012)доп =

1.0100112,
(– 45,5)доп = (– 101101,12)доп = 1.010010,12,
(– 10)доп = (– 1010)2 доп = 1.01102.
Общее правило для системы с основанием q:
каждая цифра дополняется до значения (q - 1), за исключением самой правой значащей цифры и, возможно, стоящих за ней нулей (эта цифра дополняется до значения q, а нули не изменяются).
Слайд 11

Коды для представления чисел со знаком Примеры. (– 45)доп = 1.55

Коды для представления чисел со знаком

Примеры.
(– 45)доп = 1.55 = 1.238
(–

45,5)доп = 1.54,5 = 1.22.48
(– 10)доп = 1.90
Слайд 12

Коды для представления чисел со знаком Косвенное правило: к обратному коду

Коды для представления чисел со знаком

Косвенное правило: к обратному коду отрицательного

числа надо добавить единицу в младшем разряде.
Интересной особенностью дополнительного кода является наличие единственного кода нуля:
(0)доп = (+ 0)доп = 0.0 … 0,
Это следует из косвенного правила для (– 0):
(– 0)доп = (– 0)обр + 1 = 1.1 … 12 + 1 = [1] 0.0 … 02.
Здесь в сложении участвуют все разряды, включая знаковый.
Слайд 13

Коды для представления чисел со знаком Невостребованность кодовой комбинации для (–

Коды для представления чисел со знаком

Невостребованность кодовой комбинации для (– 0)

позволяет несколько расширить диапазон значений, представимых в дополнительном коде.
Наибольшее по абсолютной величине отрицательное число имеет при общем количестве цифровых разрядов дополнительного кода n значение (– 2n):
(– 2n)доп = (– 1 0 … 02) = 1.0 … 02.
 
n n
Слайд 14

Коды для представления чисел со знаком Это следует хотя бы из

Коды для представления чисел со знаком

Это следует хотя бы из логики

такой числовой последовательности:
(– 6)доп = (– 1102)доп = 1.0102
(–7)доп = (–1112)доп = 1.0012
(–8 = –23)доп = (–10002)доп = 1.0002
Здесь справа – последовательные убывающие двоичные числа (точка-разделитель игнорируется).
Каждый из трех видов кода имеет модификацию.
В модифицированном коде – не один, а два знаковых разряда. Они имеют одинаковые значения (00 или 11).
Слайд 15

Формы представления чисел в ЭВМ Классификацию числовых форматов можно провести по

Формы представления чисел в ЭВМ

Классификацию числовых форматов можно провести по

трем признакам:
– основание системы счисления;
– наличие дробной части (целые или дробные числа);
– наличие экспоненциального множителя (числа с фиксированной или плавающей запятой).
Слайд 16

Формы представления чисел в ЭВМ В ЭВМ используются обычно 3 –

Формы представления чисел в ЭВМ

В ЭВМ используются обычно 3 –

4 формата:
целые числа (двоичные; запятая фиксирована после младшего разряда);
числа с фиксированной запятой (двоичные; дробные; запятая фиксирована после знакового разряда);
числа с плавающей запятой (двоичные; дробные; имеются мантисса и порядок – показатель степени основания системы счисления);
десятичные числа (целые; запятая фиксирована после младшего разряда).
Слайд 17

Формы представления чисел в ЭВМ В современных ЭВМ «классический формат» с

Формы представления чисел в ЭВМ

В современных ЭВМ «классический формат» с

фиксированной запятой не используется. Его роль вполне реализует формат целых чисел (рис.1).
Кстати, при выполнении арифметических операций разница между этими форматами проявляется только на уровне умножения и деления. Код – дополнительный.
Рис. 1. Пример формата «целые числа»
Слайд 18

Формы представления чисел в ЭВМ Двоичные числа с плавающей запятой (рис.

Формы представления чисел в ЭВМ

Двоичные числа с плавающей запятой (рис.

2) имеют мантиссу (mx) и порядок (рх):
X = mx * 2Рx
Рис. 2. Пример формата с плавающей запятой
Слайд 19

Формы представления чисел в ЭВМ Мантисса числа – это правильная дробь

Формы представления чисел в ЭВМ

Мантисса числа – это правильная дробь

(|mx| < 1), представлена в прямом коде Знаковый разряд ее, или, что то же, знаковый разряд числа, – разряд {31}. Количество цифровых разрядов мантиссы в примере – 24.
Характеристика представляет собою число без знака (≥ 0), а именно – порядок, смешенный в неотрицательную область:
Нх = рх + 64 = 0...127,
рх = Нх – 64 = –64 … 63.
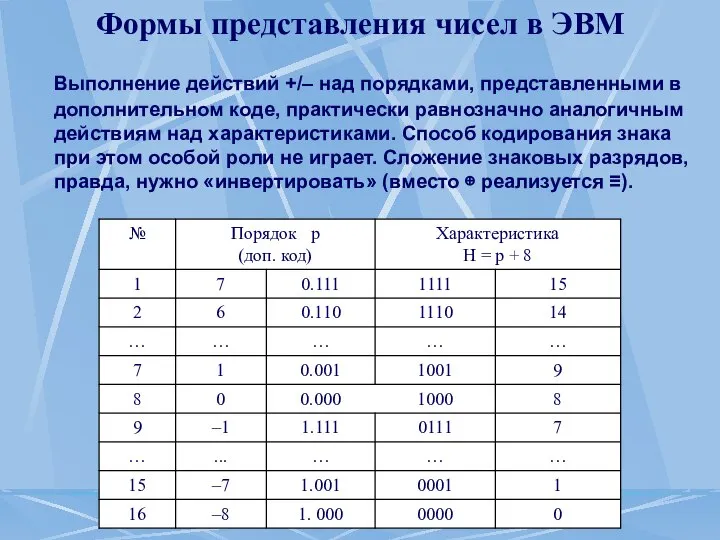
Слайд 20

Формы представления чисел в ЭВМ Выполнение действий +/– над порядками, представленными

Формы представления чисел в ЭВМ

Выполнение действий +/– над порядками, представленными

в дополнительном коде, практически равнозначно аналогичным действиям над характеристиками. Способ кодирования знака при этом особой роли не играет. Сложение знаковых разрядов, правда, нужно «инвертировать» (вместо ⊕ реализуется ≡).
Слайд 21

Формы представления чисел в ЭВМ Наибольшей точности числа с плавающей запятой

Формы представления чисел в ЭВМ

Наибольшей точности числа с плавающей запятой

соответствует его нормализованное представление:
2–1 ≤ ⏐mx⏐< 1.
Таким образом, старшая двоичная цифра мантиссы должна быть единицей.
Слайд 22

Формы представления чисел в ЭВМ Десятичные числа в старых «больших» машинах

Формы представления чисел в ЭВМ

Десятичные числа в старых «больших» машинах

(ЕС ЭВМ) представлены полями переменной длины – от 1 до 16 байтов. Ввод-вывод их осуществляется в распакованном (неупакованном, зонном) Z-формате (рис3.а), а обработка – в упакованном Р-формате (рис. 3б).
Рис. 3. Форматы десятичных чисел
Слайд 23

Формы представления чисел в ЭВМ «Зона» в неупакованном формате – это

Формы представления чисел в ЭВМ

«Зона» в неупакованном формате – это

11112 = F16.
Вместе с последующей двоичной тетрадой, представляющей десятичную цифру, зона образует байт символа, кодируемого в ДКОИ («Двоичный код обмена информацией»).
Код знака (в последнем, младшем байте) С, Е или Р16 для « + » и D16 для « – ».
В упакованном формате каждый байт, кроме последнего, содержит 2 десятичных цифры. Это означает, что десятичный операнд может иметь от 1 до 31 разряда.
Слайд 24

Формы представления чисел в ЭВМ Код для чисел со знаком –

Формы представления чисел в ЭВМ

Код для чисел со знаком –

прямой.
Самое правое положение тетрады знака благоприятствует побайтному (последовательно-параллель­ному) выполнению арифметической операции, начинающейся с младших разрядов операндов.
В алгебраическом сложении используется дополнительный код, и для преобразования отрицательных операндов и результатов «прямой-дополнительный-прямой» требуется значительное время.
Слайд 25

Диапазон и точность представления чисел Диапазон представления целых ч и с

Диапазон и точность представления чисел

Диапазон представления целых ч и с

е л, заданных в формате {0:n} (n – количество цифровых разрядов, равное 15 для случая рис. 1), определяется двояко:
Хmin ≤ X ≤ Хmax
0 ≠ ⏐X⏐min ≤ ⏐X⏐≤ ⏐X⏐max
Учитывая особенность представления максимальных по абсолютной величине отрицательных чисел в дополнительном коде, получаем:
Хmin = –2n, Хmax = –2n–1
⏐X⏐min = 1, ⏐X⏐max = 2n,
Слайд 26

Диапазон и точность представления чисел Для n = 15 (рис.1) находим:

Диапазон и точность представления чисел

Для n = 15 (рис.1) находим:
–215

= –32 768 ≤ X ≤ 215 – 1 = 32 767,
1 ≤ ⏐X⏐ ≤ 32 768.
Машинное представление здесь таково:
(Хmin) доп = 1.0 … 02

n
(Хmax) доп = 0.1 … 12

n
Слайд 27

Диапазон и точность представления чисел Точность представления чисел связывается обычно с

Диапазон и точность представления чисел

Точность представления чисел связывается обычно с

количеством значащих цифр (двоичных, десятичных, ...).
Для целых форматов оценка этой точности фактически равнозначна оценке диапазона. Она определяется n двоичными разрядами.
Для получения более привычной десятичной оценки можно воспользоваться естественным соотношением:
2x ≈ 10y,
X lg 2 ≈ y,
у ≈ 0,3010 х ≈ 0,3 х.
Десятичная точность целых форматов – 0,3n.
Например, 15 х 0,3 = 4,5.
Слайд 28

Диапазон и точность представления чисел Диапазон для чисел с плавающей запятой

Диапазон и точность представления чисел

Диапазон для чисел с плавающей запятой

абсолютно симметричен (в силу прямого кода мантиссы):
⏐Xmin ⏐= ⏐Xmax⏐ = ⏐X⏐max,
Поэтому здесь интерес представляет только диапазон для модуля:
⏐X ⏐min норм ≤ ⏐X⏐≤ ⏐X⏐max.
Индекс «норм» означает нормализованность чисел с плавающей запятой:
2–1 ≤ ⏐mx⏐ < 1.
Старшая двоичная цифра мантиссы должна быть 1.
Слайд 29

Диапазон и точность представления чисел ⏐X ⏐min норм ≤ 2–1 *

Диапазон и точность представления чисел


⏐X ⏐min норм ≤ 2–1 *

2–64 = 2–65 ≈ 10–19.
⏐X ⏐max = (1 – 2–n m ) * 263 ≈ 263 ≈ 1019.
Здесь nm – количество двоичных цифровых разрядов мантиссы
(на рис.2 их 24).
!!! Разрядность мантиссы существенно определяет точность чисел с плавающей запятой.
Слайд 30

Диапазон и точность представления чисел Значащие цифры числа, независимо от его

Диапазон и точность представления чисел

Значащие цифры числа, независимо от его

представления, – это значащие цифры мантиссы.
24-разрядная мантисса (рис. 2) соответствует точности 7 десятичных цифр.
Диапазон и точность представления десятичных чисел, как и чисел с фиксированной запятой (в частности, целых), оцениваются одинаково – длиной формата. Оценка для симметричного диапазона в случае упакованного 16-байтного формата (рис. 3):
0 ≠ 1 ≤ | х | ≤ 1031 – 1,
для точности – 31 десятичная цифра.
Слайд 31

Сложение и вычитание чисел с фиксированной запятой Сложение и вычитание представляют

Сложение и вычитание чисел с фиксированной запятой

Сложение и вычитание представляют

пару операций «типа сложения», т.е. алгебраическое сложение, которое, в свою очередь, можно понимать как сложение чисел со знаком, заданных в обратном или дополнительном коде.
Вычитание может выполняться непосредственно (с использованием, например, специальных операционных элементов – вычитателей) или косвенно, путем сведения его к сложению:
Z : = X – Y = X + (–Y)
Слайд 32

Сложение и вычитание чисел с фиксированной запятой В последнем случае достаточно,

Сложение и вычитание чисел с фиксированной запятой

В последнем случае достаточно,

как видно, изменить знак второго операнда. Если операнды (и результат) представлены в дополнительном коде, изменение знака производится путем инверсии всех разрядов и добавления 1 в младшем разряде. Например,
Y = 5 ~ 0.1012
–Y = –5 ~ 1 0102
+ ____1
1.0112 = (–5)доп,
и наоборот,
Y = –5 ~ 1.0112
–Y = 5 ~ 0 1002
+ ____1
0.1012 = (5)доп.
Слайд 33

Сложение и вычитание чисел с фиксированной запятой Правила алгебраического сложения чисел

Сложение и вычитание чисел с фиксированной запятой

Правила алгебраического сложения чисел

в обратном и дополнительном кодах тривиальны: обратные или дополнительные коды операндов суммируются как обыкновенные числа без знака, возможная единица переноса из знакового разряда (старшего знакового разряда, если код модифицированный) циклически переносится в младший разряд для второго суммирования (обратный код) или отбрасывается (дополнительный код).
« + » – знак операции сложения с циклическим переносом (Пример 1).
Слайд 34

Сложение и вычитание чисел с фиксированной запятой Пример 1. Х =

Сложение и вычитание чисел с фиксированной запятой

Пример 1.
Х = –5

Xобр = 1.0102
+ +
Y = 7 Yобр = 0.1112
__________ ____________
Z = 2 10.001
+ 1
____________
Zобр = 0.0102
Слайд 35

Сложение и вычитание чисел с фиксированной запятой Пример 2. Х =

Сложение и вычитание чисел с фиксированной запятой

Пример 2.
Х = 5

Xдоп мод = 00.1012
+ +
Y = -7 Yдоп мод = 11.0012
__________ ____________
Z = -2 Zдоп мод = 11.1102
Слайд 36

Сложение и вычитание чисел с фиксированной запятой Вообще, при сложении чисел

Сложение и вычитание чисел с фиксированной запятой

Вообще, при сложении чисел

с разными знаками в дополнительном коде отсутствие переноса свидетельствует об отрицательном результате (как в Примере 2), а наличие – о результате положительном или нулевом (Пример 3).
Пример 3.
Х = 5 Xдоп = 0.1012
+ +
Y = -5 Yдоп = 1.0112
__________ ____________
Z = 0 Zдоп = 10.0102
рвых = 1
Слайд 37

Сложение и вычитание чисел с фиксированной запятой В обратном коде отсутствие

Сложение и вычитание чисел с фиксированной запятой

В обратном коде отсутствие

выходного переноса свидетельствует о неположительном результате (Пример 4), а наличие его – о результате положительном (Пример 1).
Пример 4.
Х = 5 Xобр = 0.1012
+ +
Y = -5 Yдоп = 1.0102
__________ ____________
Z = 0 Zобр = 1.1112 = (- 0)обр
рвых = 0
Слайд 38

Сложение и вычитание чисел с фиксированной запятой Обнаружение переполнения разрядной сетки

Сложение и вычитание чисел с фиксированной запятой

Обнаружение переполнения разрядной сетки

при сложении может производиться несколькими способами.
Самый простой способ – использование модифицированного кода (с двумя знаковыми разрядами).
Старший знаковый разряд даже при переполнении сохраняет информацию о знаке результата («Разряд знака»).
Младший – «Разряд переполнения». Комбинация знаков при «положительном» переполнении – 01,
при «отрицательном» – 10.
Слайд 39

Сложение и вычитание чисел с фиксированной запятой Пример 5. Х =

Сложение и вычитание чисел с фиксированной запятой

Пример 5.
Х =

3 Xдоп мод = 00.0112
+ +
Y = 6 Yдоп мод = 00.1102
__________ ____________
Z = 9 > 7 Zдоп мод ~ 01.0012 (положительное
переполнение)
Пример 6.
х = - 3 Xдоп мод = 11.1012
+ +
у = - 6 Yдоп мод = 11.0102
__________ ____________
z = - 9 < 8 Zдоп мод ~ 10.1112 (отрицательное
переполнение)
Слайд 40

Сложение и вычитание чисел с фиксированной запятой В примере 6 указано

Сложение и вычитание чисел с фиксированной запятой

В примере 6 указано

граничное значение (- 8), которое может быть представлено без переполнения:
(-8) доп мод = 11.0002
Недостаток способа модифицированного кода — расширение разрядной сетки на один разряд.
Слайд 41

Сложение и вычитание чисел с фиксированной запятой Второй способ обнаружения переполнения

Сложение и вычитание чисел с фиксированной запятой

Второй способ обнаружения переполнения

- сравнение переносов в знаковый разряд и из знакового разряда. Переполнение - при несовпадении этих переносов. Фактически здесь тоже «задействован» модифицированный дополнительный код.
Случай А. Неотрицательные операнды.
Слайд 42

Сложение и вычитание чисел с фиксированной запятой Правило сравнения переносов дает

Сложение и вычитание чисел с фиксированной запятой

Правило сравнения переносов дает

значение признака переполнения:
φр = 0 ⊕ X = X
(переполнение при X = 1).
Слева от штриховой черты показаны значения воображаемого модифицированного дополнительного кода. Правило этого способа дает такое же значение признака переполнения:
φм = 0 ⊕ X = X
Слайд 43

Сложение и вычитание чисел с фиксированной запятой Случай В. Отрицательные операнды.

Сложение и вычитание чисел с фиксированной запятой

Случай В. Отрицательные операнды.
Здесь

тоже φр = φм = 1 ⊕ X = X
(переполнение может быть только отрицательное - при отсутствии переноса из старшего цифрового разряда).
Слайд 44

Сложение и вычитание чисел с фиксированной запятой Случай С. Операнды имеют

Сложение и вычитание чисел с фиксированной запятой

Случай С. Операнды имеют

разные знаки
Оба признака переполнения снова совпадают, они имеют нулевые значения (переполнение в принципе невозможно):
φр = Х ⊕ X = 0
φм = Х ⊕ X = 0
Слайд 45

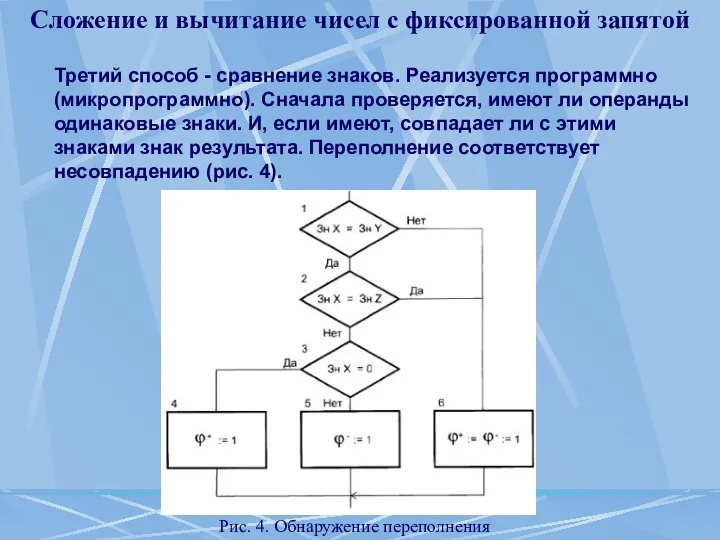
Сложение и вычитание чисел с фиксированной запятой Третий способ - сравнение

Сложение и вычитание чисел с фиксированной запятой

Третий способ - сравнение

знаков. Реализуется программно (микропрограммно). Сначала проверяется, имеют ли операнды одинаковые знаки. И, если имеют, совпадает ли с этими знаками знак результата. Переполнение соответствует несовпадению (рис. 4).

Рис. 4. Обнаружение переполнения

- Предыдущая
Эндокринная офтальмопатия
Следующая -
Аттестационная работа. программа внеурочной деятельности Я - исследователь. (5-6 класс)

Похожие презентации

Теория автоматов и формальных языков
Системы хранения данных OceanStor 5300 V3 и 5500 V3
Абстрактные типы данных. Структура данных
Министерство образования и науки Республики Башкортостан Государственное бюджетное
Итоги работы 1Q 2022
Сеть между компьютерами
Прямая адресация памяти
Introduction of kns55 platform
Знакомство с электронными таблицами MICROSOFT EXCEL
Аддитивное производство (3D печать)
Свойства объектов и слои
Сравнительный анализ (ПланФикс, Мегаплан, Модуль 1C:PM Управление проектами для 1С:ERP)
Криптотұрақтылығы
Мои любимые компьютерные игры
Фон технологии
Работа с базой данных
Операционные системы
Средства вычислительной техники
Компьютерная графика и области её применения
Непозиційні системи числення
Вирусы и антивирусные системы
Подходы к определению и единицы измерения
Списки. Лекция 6
Воробей. Игра
UI/UX дизайн в играх: Влияние на погружение
Списки в html-документах
Электронные таблицы Excel
Решение задачи №8 Линейный алгоритм. Информатика ОГЭ 9 класс
Вы можете прислать нам Вашу презентацию и мы опубликуем ее на сайте.
Обратная связь
Для правообладателей
Email: Нажмите что бы посмотреть