Содержание
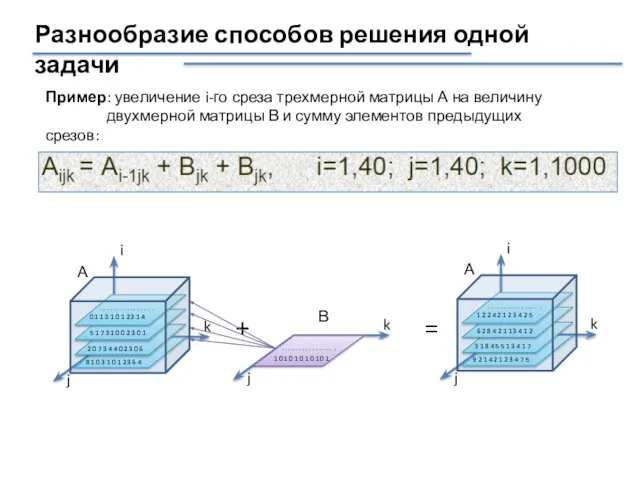
- 2. Разнообразие способов решения одной задачи Пример: увеличение i-го среза трехмерной матрицы А на величину двухмерной матрицы
- 3. Способ 1 организации суммирования
- 4. Способ 2 организации суммирования
- 5. Пример 2 Умножение матриц 1. Возможен ли другой порядок? 2. Нужен ли другой порядок?
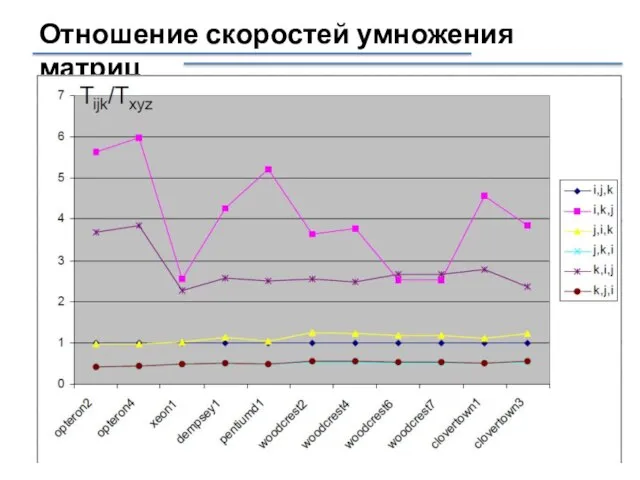
- 6. Отношение скоростей умножения матриц
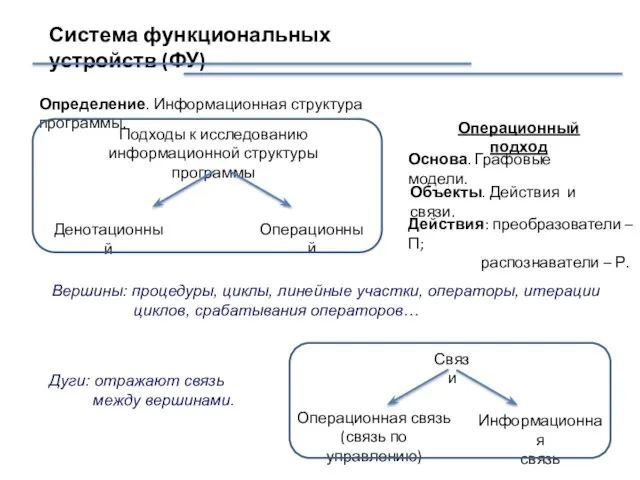
- 7. Система функциональных устройств (ФУ) Определение. Информационная структура программы. Подходы к исследованию информационной структуры программы Денотационный Операционный
- 8. Операционная связь Дуги: операционная связь Две вершины A и B соединяются направленной дугой тогда и только
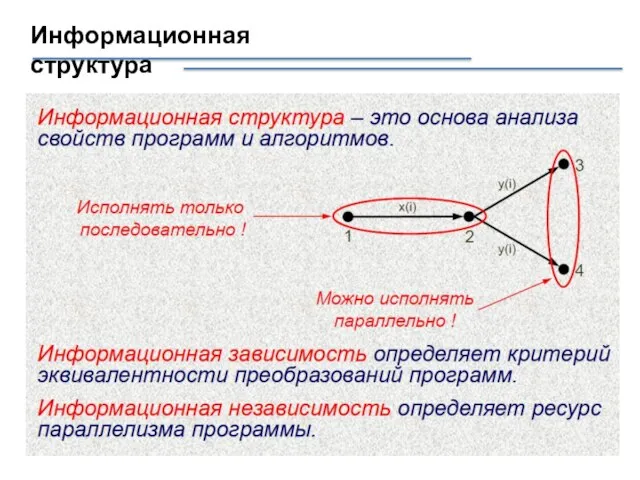
- 9. Информационная связь Дуги: информационная связь Две вершины A и B соединяются направленной дугой B тогда и
- 10. Пример: Система линейных уравнений Дано: СЛАУ: Ax=b; A(nxn) – левая двухдиагональная матрица; ai – диагональные элементы,
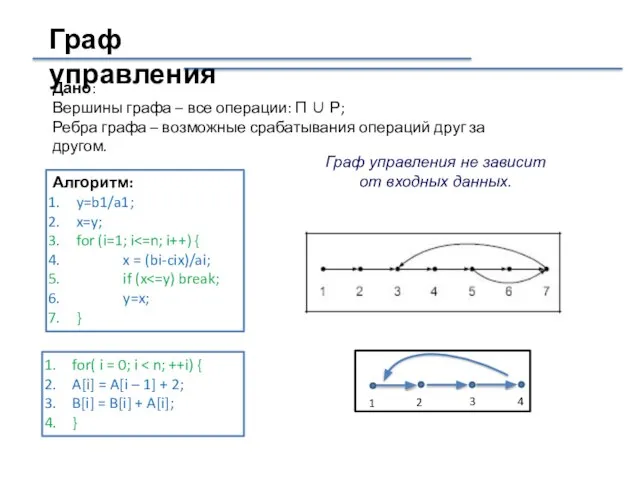
- 11. Граф управления Алгоритм: y=b1/a1; x=y; for (i=1; i x = (bi-cix)/ai; if (x y=x; } Дано:
- 12. Граф операционно-логической истории Дано: Начальные данные; Последовательный вычислитель; Вершины графа – каждое срабатывание каждой операции: П
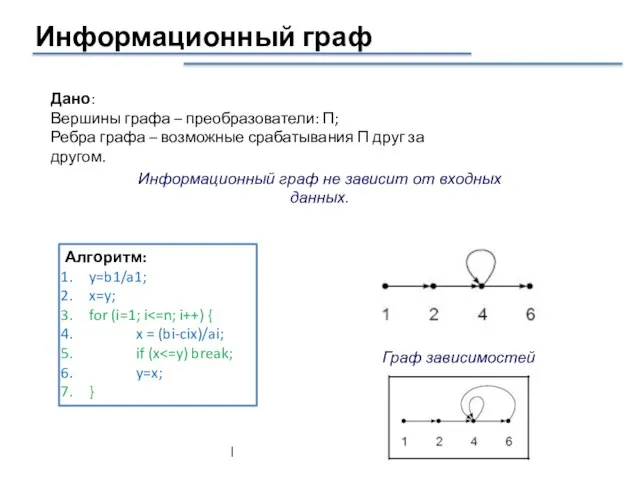
- 13. Информационный граф Дано: Вершины графа – преобразователи: П; Ребра графа – возможные срабатывания П друг за
- 14. Граф истории реализации программы Дано: Начальные данные; Последовательный вычислитель; Вершины графа – каждое срабатывание каждого преобразователя:
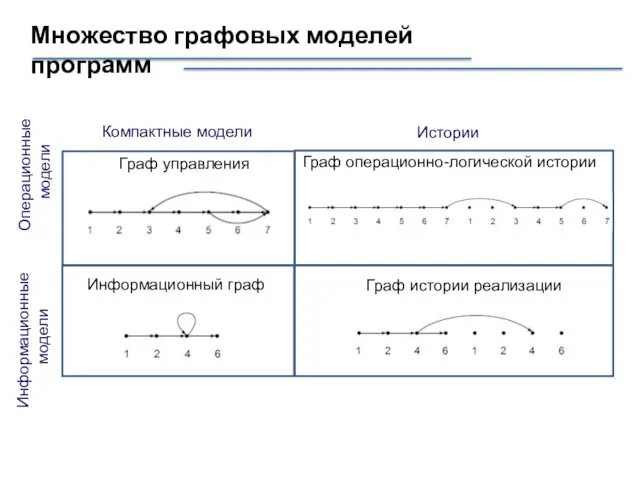
- 15. 4 графовые модели Граф управления; Граф операционно-логической истории; Информационный граф; Граф истории реализации.
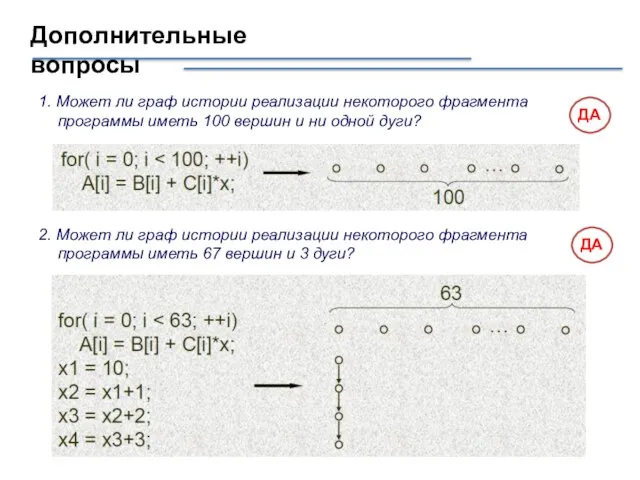
- 16. Дополнительные вопросы 1. Может ли граф истории реализации некоторого фрагмента программы иметь 100 вершин и ни
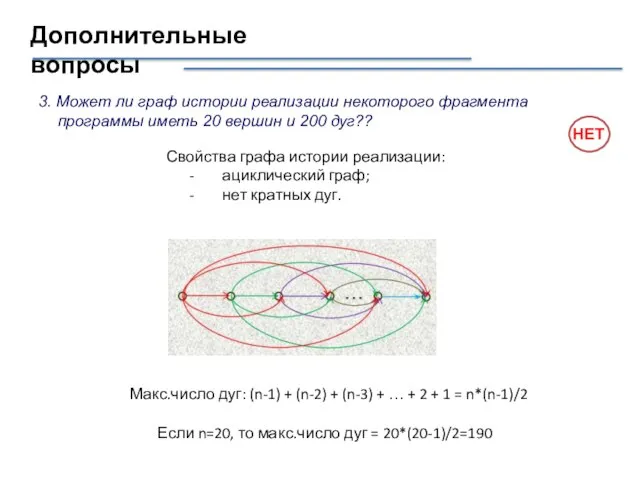
- 17. Дополнительные вопросы 3. Может ли граф истории реализации некоторого фрагмента программы иметь 20 вершин и 200
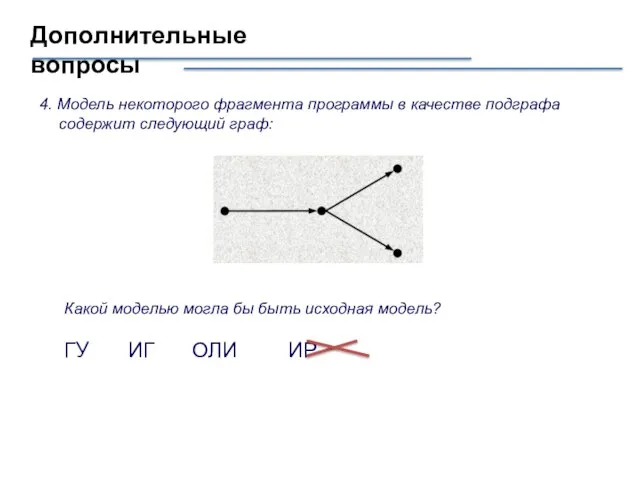
- 18. Дополнительные вопросы 4. Модель некоторого фрагмента программы в качестве подграфа содержит следующий граф: Какой моделью могла
- 19. Множество графовых моделей программ Граф управления Граф операционно-логической истории Информационный граф Граф истории реализации Операционные модели
- 20. Информационная структура
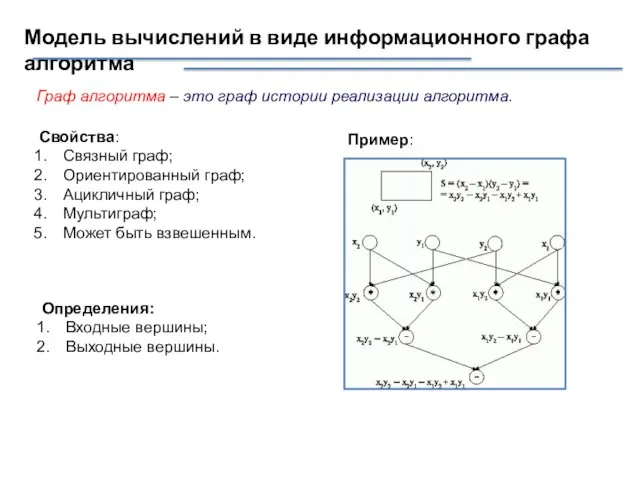
- 21. Модель вычислений в виде информационного графа алгоритма Граф алгоритма – это граф истории реализации алгоритма. Свойства:
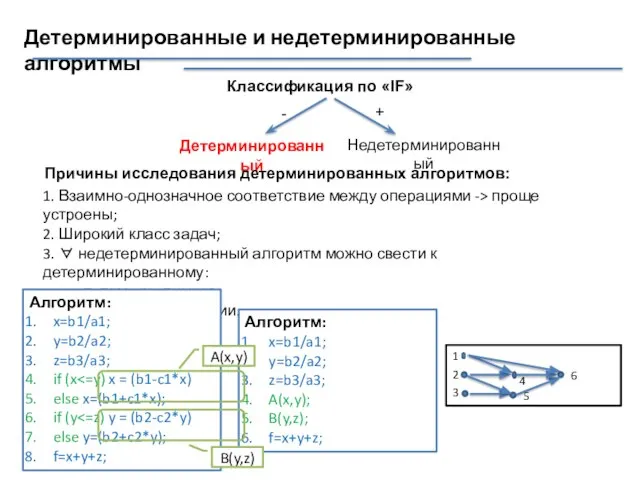
- 22. Детерминированные и недетерминированные алгоритмы Классификация по «IF» Детерминированный Недетерминированный + - 1. Взаимно-однозначное соответствие между операциями
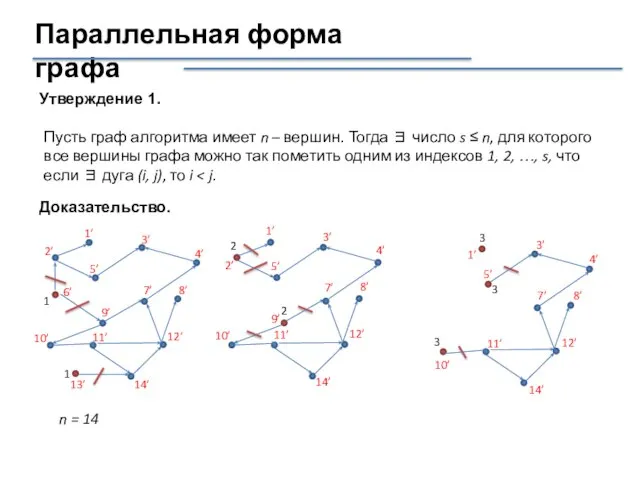
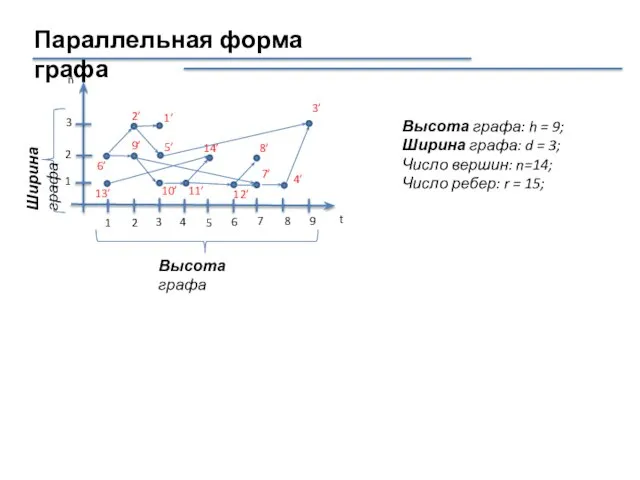
- 23. Параллельная форма графа Утверждение 1. Пусть граф алгоритма имеет n – вершин. Тогда ∃ число s
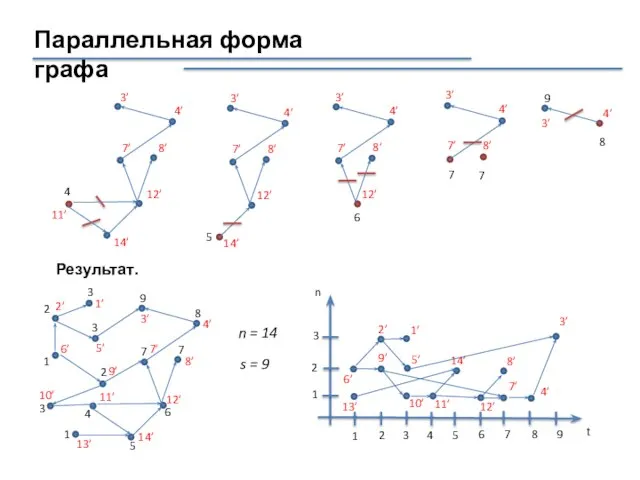
- 24. Параллельная форма графа n = 14 s = 9 Результат.
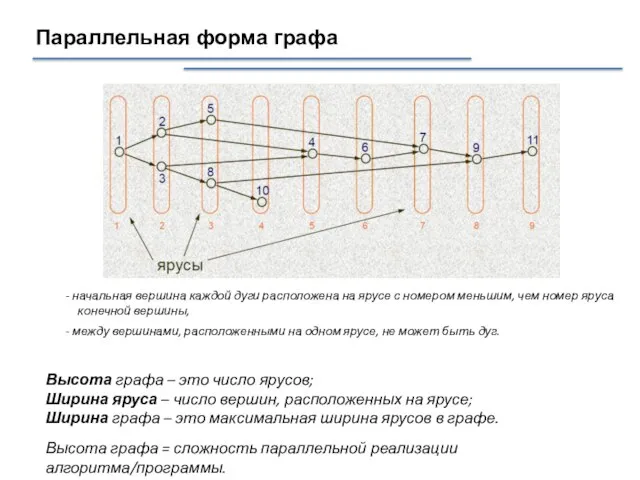
- 25. Параллельная форма графа - начальная вершина каждой дуги расположена на ярусе с номером меньшим, чем номер
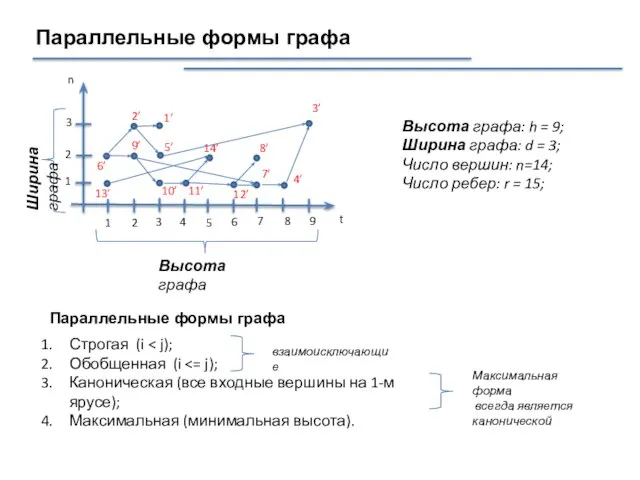
- 26. Параллельные формы графа Параллельные формы графа Строгая (i Обобщенная (i Каноническая (все входные вершины на 1-м
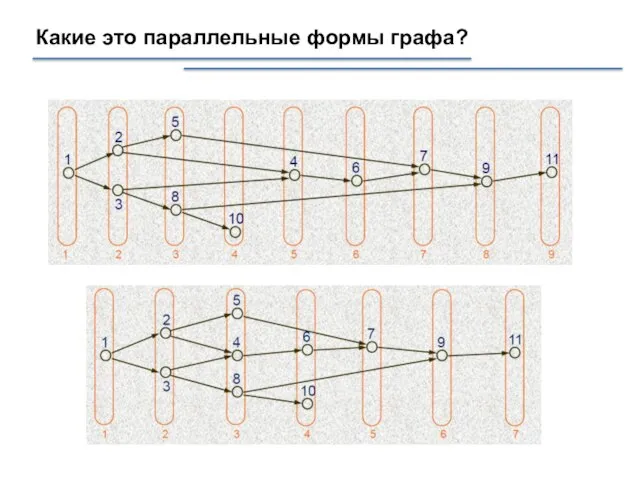
- 27. Какие это параллельные формы графа?
- 28. Ускорение по Амдалу
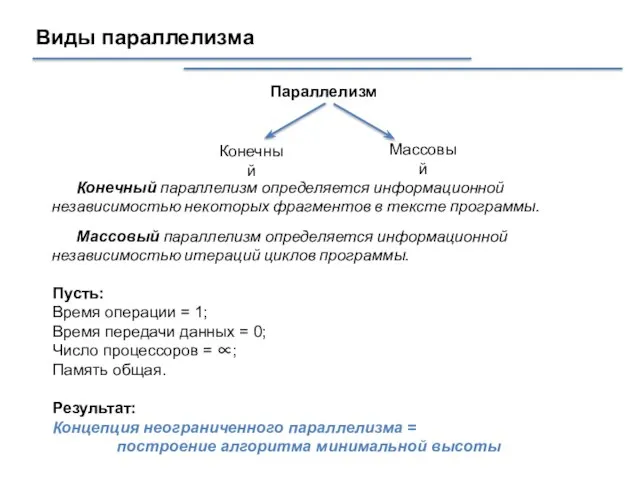
- 29. Виды параллелизма Параллелизм Конечный Массовый Конечный параллелизм определяется информационной независимостью некоторых фрагментов в тексте программы. Массовый
- 30. Пример. Произведение элементов вектора. Схема последовательного умножения:
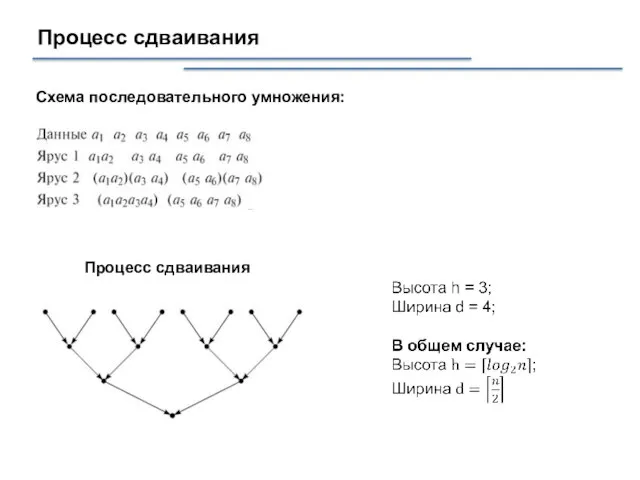
- 31. Процесс сдваивания Схема последовательного умножения: Процесс сдваивания
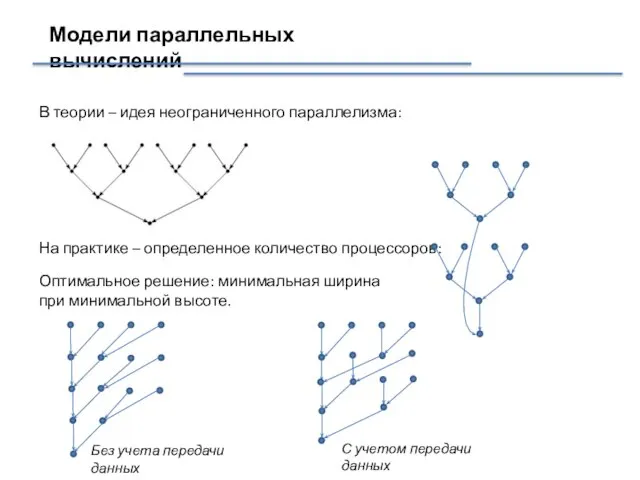
- 32. Модели параллельных вычислений В теории – идея неограниченного параллелизма: Оптимальное решение: минимальная ширина при минимальной высоте.
- 33. Параллельная форма графа Высота графа: h = 9; Ширина графа: d = 3; Число вершин: n=14;
- 34. Модели параллельных вычислений Минимальное количество необходимых процессоров = ширина графа: В этом случае: Плотность вычислений: Ускорение:
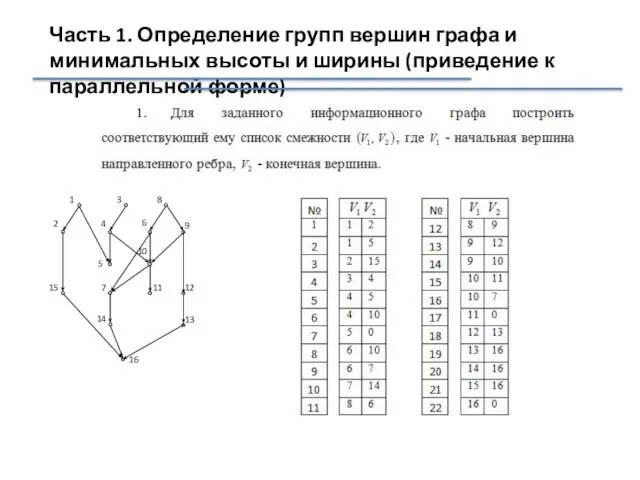
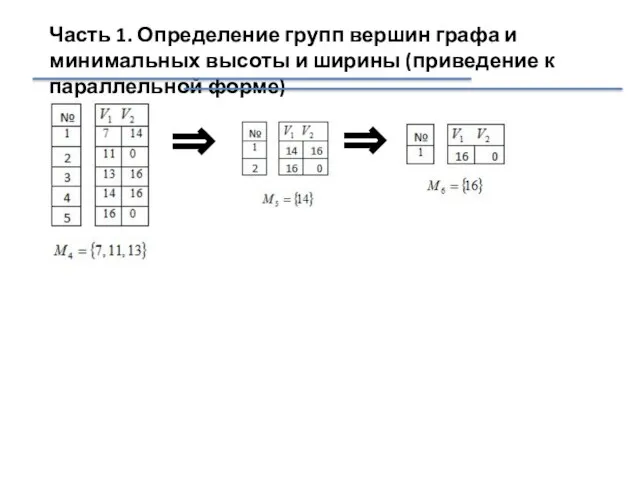
- 35. Часть 1. Определение групп вершин графа и минимальных высоты и ширины (приведение к параллельной форме)
- 36. Часть 1. Определение групп вершин графа и минимальных высоты и ширины (приведение к параллельной форме)
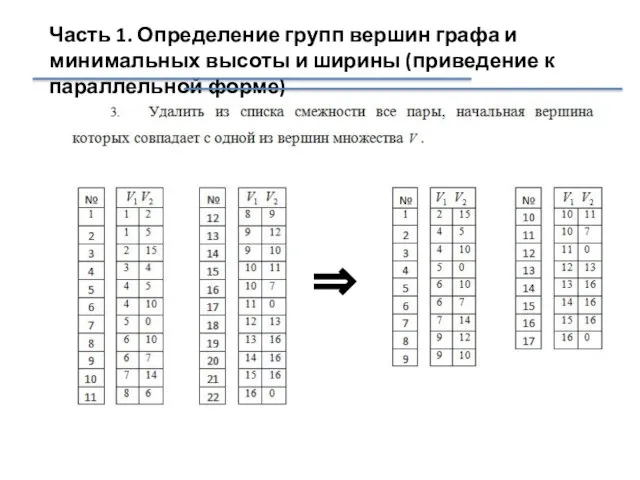
- 37. Часть 1. Определение групп вершин графа и минимальных высоты и ширины (приведение к параллельной форме) ⇒
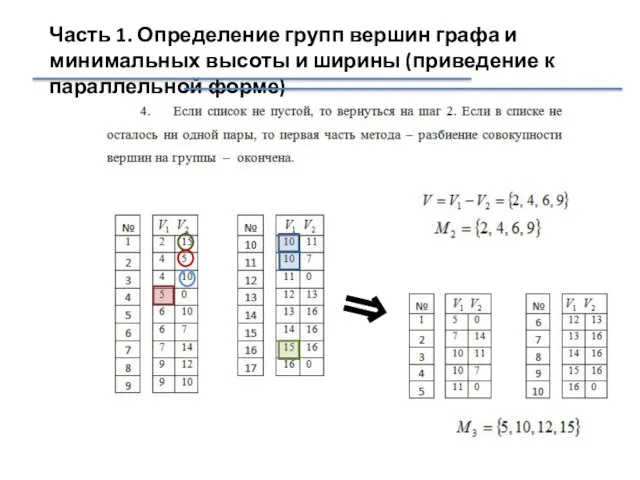
- 38. Часть 1. Определение групп вершин графа и минимальных высоты и ширины (приведение к параллельной форме) ⇒
- 39. Часть 1. Определение групп вершин графа и минимальных высоты и ширины (приведение к параллельной форме) ⇒
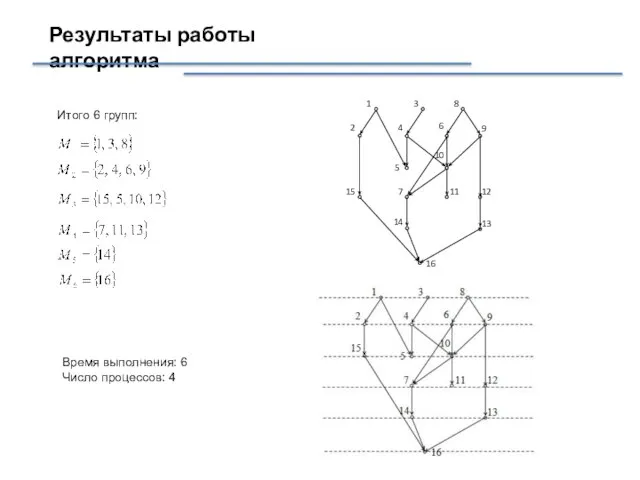
- 40. Результаты работы алгоритма Итого 6 групп: Время выполнения: 6 Число процессов: 4
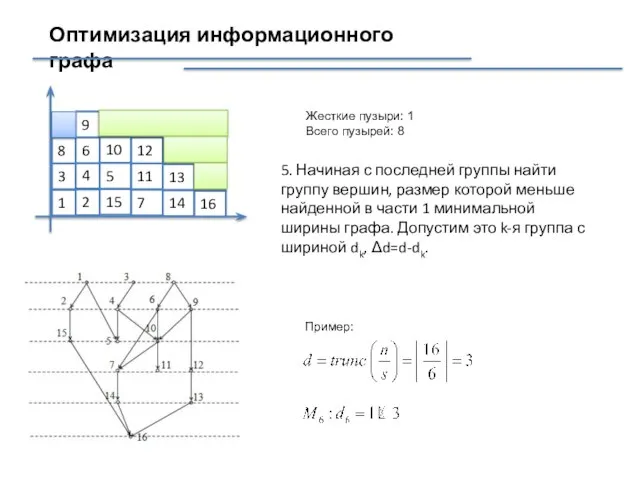
- 41. Оптимизация информационного графа Жесткие пузыри: 1 Всего пузырей: 8 5. Начиная с последней группы найти группу
- 42. Оптимизация информационного графа Ширина равна 1. Δd=d-dk=3-1=2. Добавить можем 2 элемента. M5={14}, x=14. Составляем всевозможные пары
- 43. Оптимизация информационного графа Ширина равна 1. Δd=d-dk=3-1=2. Добавить можем 2 элемента. M4={7, 11, 13}, x=7. Составляем
- 44. Оптимизация информационного графа Ширина равна 1. Δd=d-dk=3-1=2. Добавить можем 2 элемента. M3={15, 5, 10, 12}, x=15.
- 45. Оптимизация информационного графа M5={14,11,13} M4={7,5,15} M3={10,12,2} M2={4,6,9} M1={1,3,8}
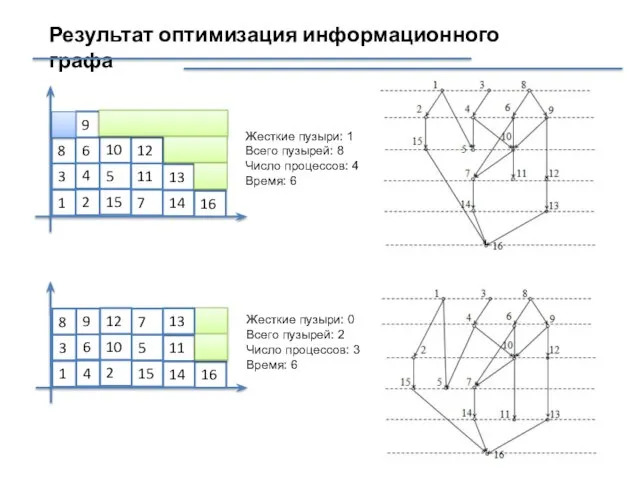
- 46. Результат оптимизация информационного графа Жесткие пузыри: 1 Всего пузырей: 8 Число процессов: 4 Время: 6 Жесткие
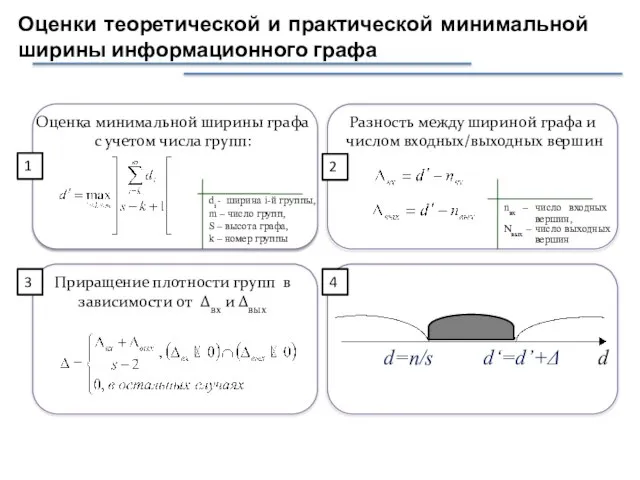
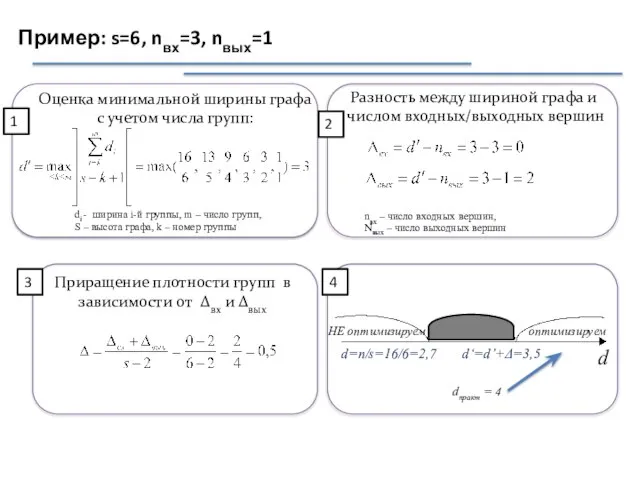
- 47. Оценка минимальной ширины графа с учетом числа групп: di - ширина i-й группы, m – число
- 48. Оценка минимальной ширины графа с учетом числа групп: di - ширина i-й группы, m – число
- 50. Скачать презентацию

















 Семинары по подготовке к Олимпиаде D-Link по сетевым технологиям
Семинары по подготовке к Олимпиаде D-Link по сетевым технологиям Комунікація як інструмент підвищення привабливості громади
Комунікація як інструмент підвищення привабливості громади Строки в языке программирования C++
Строки в языке программирования C++ Лекция 4. Ссылочные типы. Операторы цикла.
Лекция 4. Ссылочные типы. Операторы цикла.  Понятие о локальных сетях
Понятие о локальных сетях Каскадные таблицы стилей – CSS. (Тема 8)
Каскадные таблицы стилей – CSS. (Тема 8) Спам и защита от него
Спам и защита от него Система криптографического обеспечения Карма
Система криптографического обеспечения Карма Организация вычислений в электронных таблицах обработка числовой информации в электронных таблицах
Организация вычислений в электронных таблицах обработка числовой информации в электронных таблицах Проект "База данных книг"
Проект "База данных книг" Кодирование и представление информации
Кодирование и представление информации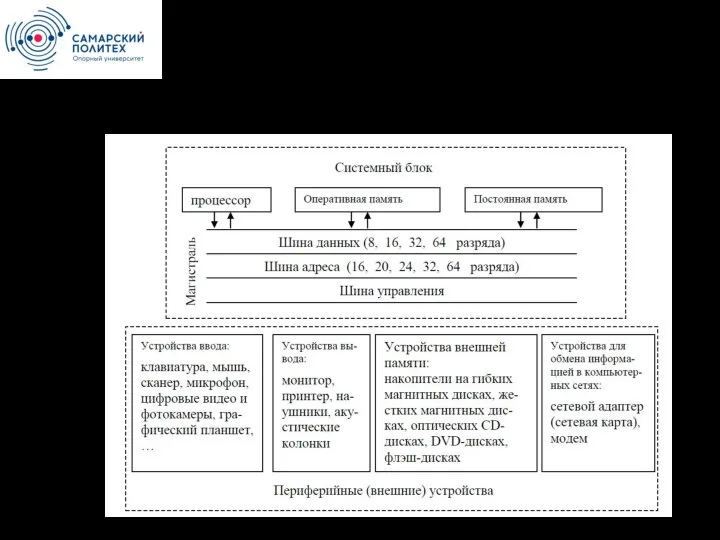 Компьютер
Компьютер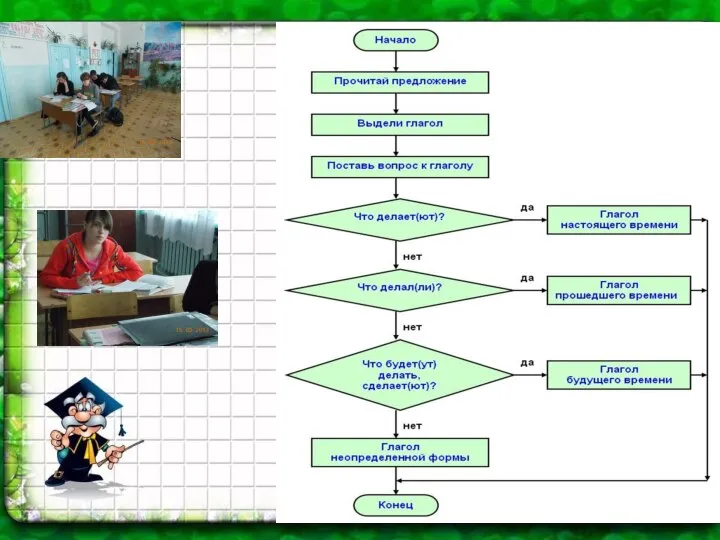 Циклический алгоритм
Циклический алгоритм Работа с информацией
Работа с информацией Разработка игр. Гейм-дизайн
Разработка игр. Гейм-дизайн Город, о котором я мечтаю
Город, о котором я мечтаю пк
пк Презентация "Применение эффектов" - скачать презентации по Информатике
Презентация "Применение эффектов" - скачать презентации по Информатике Презентация "Разработка мультимедийных приложений для MeeGo" - скачать презентации по Информатике
Презентация "Разработка мультимедийных приложений для MeeGo" - скачать презентации по Информатике Reveal the halloween picture (game)
Reveal the halloween picture (game) Интеллектуальные информационные системы. Задача о ходе коня
Интеллектуальные информационные системы. Задача о ходе коня Функции тележурналистики А.В. Земскова
Функции тележурналистики А.В. Земскова Алгоритмы и кейсы
Алгоритмы и кейсы Презентация "знания" - скачать презентации по Информатике
Презентация "знания" - скачать презентации по Информатике Использование информационно-коммуникационных технологий на уроках литературного чтения
Использование информационно-коммуникационных технологий на уроках литературного чтения Администрирование БД Системные и пользовательские БД SQL Server 2000
Администрирование БД Системные и пользовательские БД SQL Server 2000 Логика высказываний Алгоритм построения таблиц истинности Автор: Сергеев Евгений Викторович МОУ СОШ №4 г. Миньяра Челябинск
Логика высказываний Алгоритм построения таблиц истинности Автор: Сергеев Евгений Викторович МОУ СОШ №4 г. Миньяра Челябинск System buses (lecture 5)
System buses (lecture 5)