Содержание
- 2. Изучаемые вопросы Формы мышления. Алгебра высказываний. Логические выражения и функции. Основные законы алгебры логики. Примеры решения
- 3. Формы мышления. Алгебра высказываний.
- 4. Логика, как и теория алгоритмов – является теоретической основой современных ЭВМ и программирования. Слово «логика» в
- 5. Понятие – это мысль, в которой обобщаются отличительные свойства. Примеры: портфель, трапеция, ураганный ветер. Понятие имеет
- 6. СУЖДЕНИЕ – это форма мышления, в которой что-либо утверждается или отрицается об объектах, их свойствах и
- 7. Математическая логика является специальным математическим аппаратом, который лежит в основе работы логических схем и устройств персонального
- 8. Алгебру логики иначе называют алгеброй высказываний. Суждения и утверждения в математической логике называют высказываниями и предикатами.
- 9. ВЫСКАЗЫВАНИЕ - это повествовательное предложение, о котором можно сказать, что оно истинно или ложно. Например: Земля
- 10. Высказывания могут быть простыми и сложными. Высказывание считается простым, если никакую его часть нельзя рассматривать как
- 11. Сложное высказывание получается путем объединения простых высказываний логическими связками — НЕ, И, ИЛИ. Значение истинности сложных
- 12. В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание
- 13. Базовые логические операции
- 14. Над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания. Для образования
- 15. КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) соответствует союзу И обозначается знаком & или Λ, или · Конъюнкция двух логических
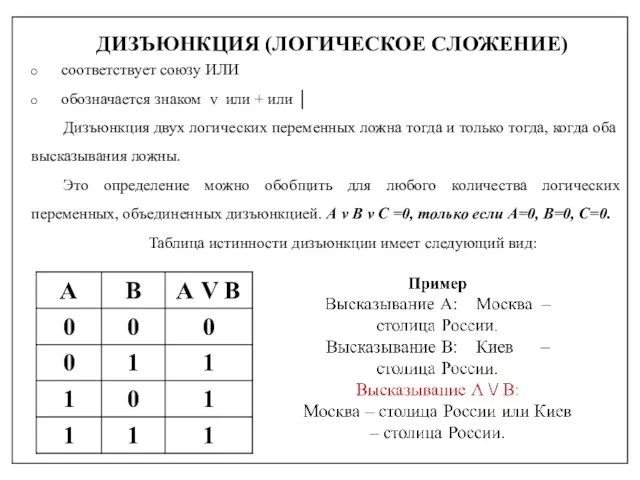
- 16. ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ) соответствует союзу ИЛИ обозначается знаком v или + или │ Дизъюнкция двух логических
- 17. ИНВЕРСИЯ (ОТРИЦАНИЕ) соответствует частице НЕ обозначается черточкой над именем переменной или знаком ¬ перед переменной Инверсия
- 18. Сложные высказывания можно представить в виде логического выражения или формулы, состоящей из логических переменных, которые обозначают
- 19. Таблицы истинности можно построить для каждого логического выражения. Она определяет его значение при всех возможных комбинациях
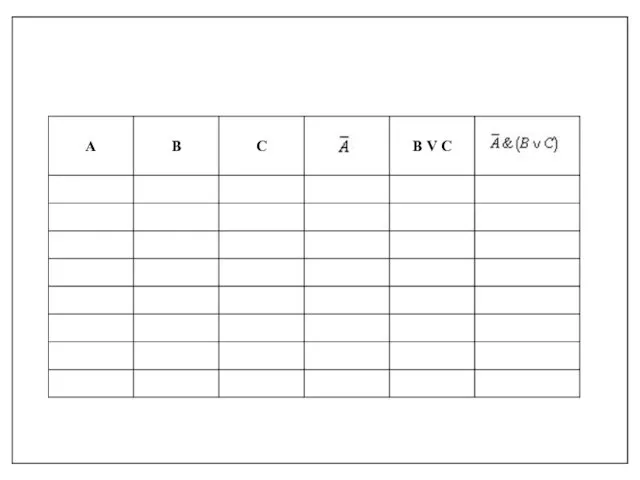
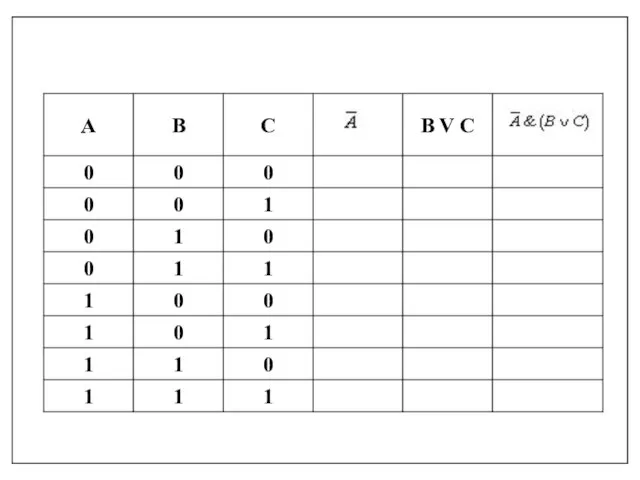
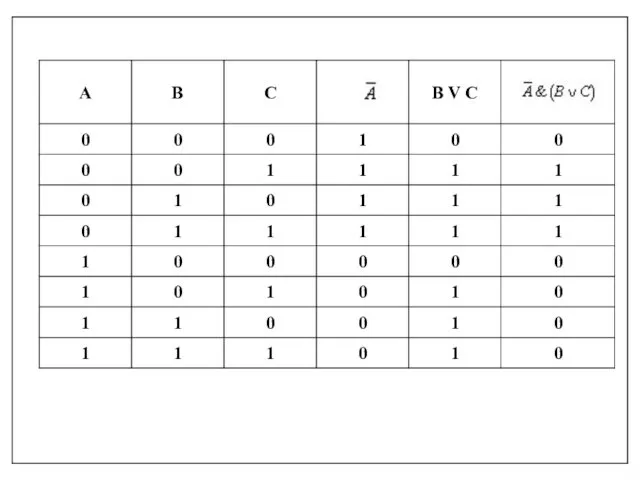
- 20. Например, построим таблицу истинности для логической функции: 1. Количество входных переменных в заданном выражении равно трем
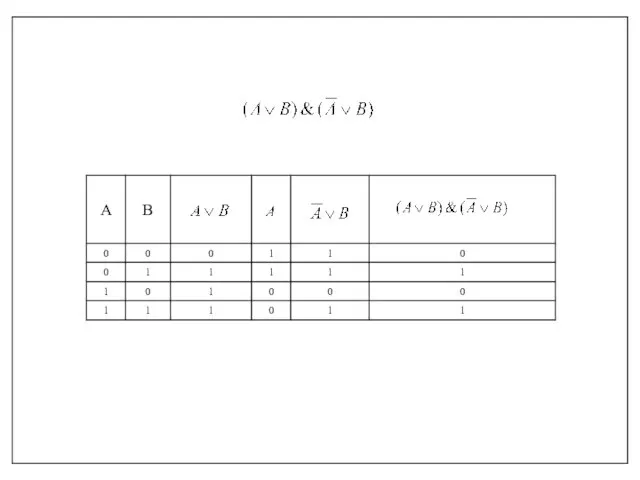
- 24. Задание 1. Постройте таблицу истинности для данного логического выражения:
- 26. Равносильные логические выражения - логические выражения, у которых совпадают последние столбцы таблиц истинности. Составное высказывание можно
- 27. Логические выражения и функции
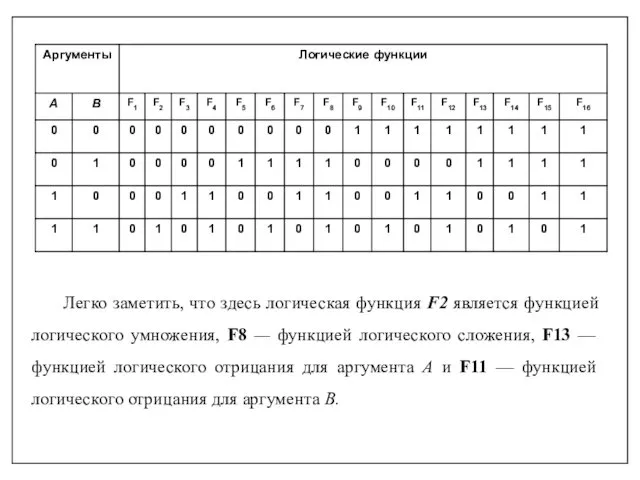
- 28. Выше были рассмотрены функции двух аргументов: логическое умножение F (A, B) = A&B, логическое сложение F
- 29. Легко заметить, что здесь логическая функция F2 является функцией логического умножения, F8 — функцией логического сложения,
- 30. В обыденной и научной речи кроме базовых логических связок «и», «или», «не» используются и некоторые другие:
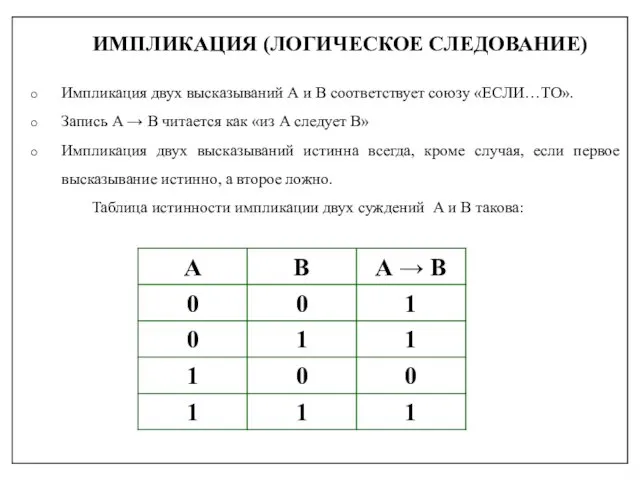
- 31. ИМПЛИКАЦИЯ (ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ) Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО». Запись А → В
- 32. ЭКВИВАЛЕНТНОСТЬ (ЛОГИЧЕСКОЕ РАВЕНСТВО, ФУНКЦИЯ ТОЖДЕСТВА) Она обозначается символами ≡ или . («тогда и только тогда»). Запись
- 33. В алгебре высказываний все логические функции могут быть сведены путём логических преобразований к трём базовым логическим
- 34. Основные законы алгебры логики
- 35. Равносильности формул логики высказываний часто называют законами логики. Законы логики отражают наиболее важные закономерности логического мышления.
- 36. 1. Закон тождества. Всякое высказывание тождественно самому себе: Закон тождества утверждает, что мысль, заключенная в некотором
- 37. 3. Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает,
- 38. 4. Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание:
- 39. 5. Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых «сомножителей» равносильна одному
- 40. 7. Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно
- 41. 9. Правило дистрибутивности. В отличие от обычной алгебры, где за скобки можно выносить только общие множители,
- 42. РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ
- 43. 1. Какое из предложений является высказыванием: а) Не можете ли вы передать мне соль? б) Некоторые
- 44. 2. Составьте отрицания к данным высказываниям: а) Все дни в августе были солнечными б) Не все
- 46. Скачать презентацию




































 Презентация на тему Wi-Fi
Презентация на тему Wi-Fi  Дети вне интернет-зависимости
Дети вне интернет-зависимости Информация. Виды информации
Информация. Виды информации Автоматизированная система управления технологическим процессом
Автоматизированная система управления технологическим процессом Передача и хранение информации. 10 класс
Передача и хранение информации. 10 класс არარეზიდენტი
არარეზიდენტი Компьютерные программы (4 класс)
Компьютерные программы (4 класс) Введение в программную инженерию технологии промышленной разработки программного обеспечения
Введение в программную инженерию технологии промышленной разработки программного обеспечения Телевидение, радио и интернет в нашей жизни. О пользе и вреде современных медиа
Телевидение, радио и интернет в нашей жизни. О пользе и вреде современных медиа Устройство ЭВМ
Устройство ЭВМ Технология подучения, хранения и передачи информации
Технология подучения, хранения и передачи информации Как вести себя на улице 1 класс
Как вести себя на улице 1 класс Моделирование. 4 класс
Моделирование. 4 класс Интернет без правды и лжи
Интернет без правды и лжи Атняшева Гульнария Борисовна Учитель математики и информатики МБОУ «Канабековская ООШ» с.Канабеки г. Лысьва Пермский край
Атняшева Гульнария Борисовна Учитель математики и информатики МБОУ «Канабековская ООШ» с.Канабеки г. Лысьва Пермский край Информационный видеосервис для разработчиков программного обеспечения. SEO-перезагрузка
Информационный видеосервис для разработчиков программного обеспечения. SEO-перезагрузка Изучение программы PowerPoint
Изучение программы PowerPoint SQL. Часть 1
SQL. Часть 1 Операционная система
Операционная система Введение в Python
Введение в Python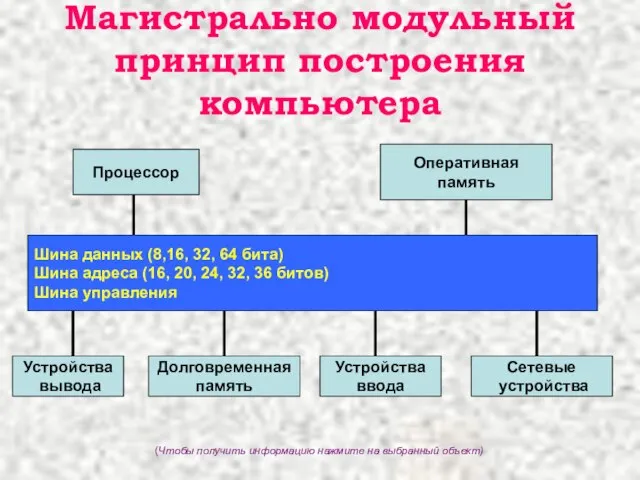 Магистрально модульный принцип построения компьютера
Магистрально модульный принцип построения компьютера Метапредметные результаты. Компетентностноориентированные задания
Метапредметные результаты. Компетентностноориентированные задания Устройство компьютера
Устройство компьютера Дисциплина «Информатика» Преподаватель: Бедрина Светлана Львовна
Дисциплина «Информатика» Преподаватель: Бедрина Светлана Львовна  Моделирование, формализация, визуализация
Моделирование, формализация, визуализация 3b902ed90b9e410a96c63a08603b700f
3b902ed90b9e410a96c63a08603b700f HTML. Сайт
HTML. Сайт ОПЕРАЦИОННАЯ СИСТЕМА КОМПЬЮТЕРА
ОПЕРАЦИОННАЯ СИСТЕМА КОМПЬЮТЕРА