Содержание
- 2. Основные формы мышления: Понятие – форма мышления, фиксирующая основные существенные признаки объекта. Понятие имеет: Содержание –
- 3. Объем понятия может быть представлено в форме множества объектов, состоящего из элементов множества. Алгебра множеств, одна
- 4. Совокупность всех существующих множеств образует всеобщее универсальное множество 1, которое позволяет отобразить множество логически противоположное к
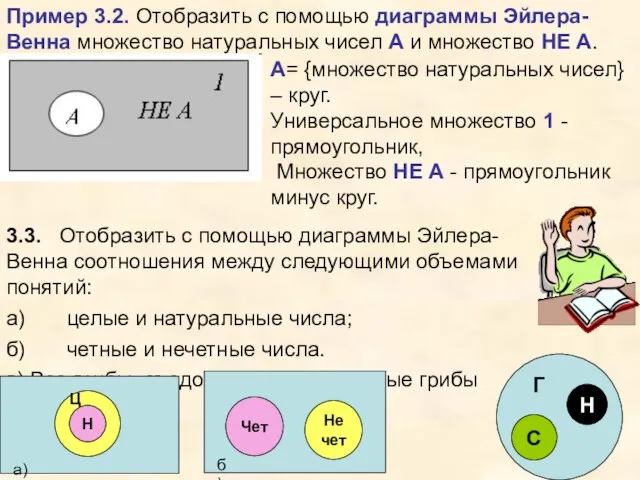
- 5. Пример 3.2. Отобразить с помощью диаграммы Эйлера-Венна множество натуральных чисел А и множество НЕ А. А=
- 6. Высказывание - это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и
- 7. Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено
- 8. Англичанин Джордж Буль (1815-1864, математик-самоучка), на фундаменте, заложенном Лейбницем, создал новую область науки - Математическую логику
- 9. Алгебра логики (высказываний) работает с высказываниями. Различают: Логические константы (логические утверждения) – конкретные частные утверждения (И/Л)
- 10. 3. Логические функции ( логические формулы) – сложные логические выражения образованных из простых и связанных логическими
- 11. Логические операции Отрицание (инверсия). Обозначение: НЕ А, ¬А, А={Дети любят игрушки} = {Дети НЕ любят игрушки}
- 12. 2. Логическое умножение (Конъюнкция) Обозначение: И, ∧, &, • F=A ^ B= {кит, акула, дельфин} Таблица
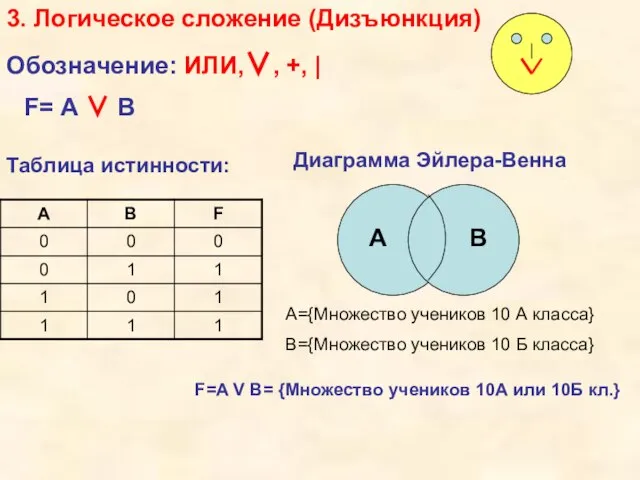
- 13. 3. Логическое сложение (Дизъюнкция) Обозначение: ИЛИ,∨, +, | F=A V B= {Множество учеников 10А или 10Б
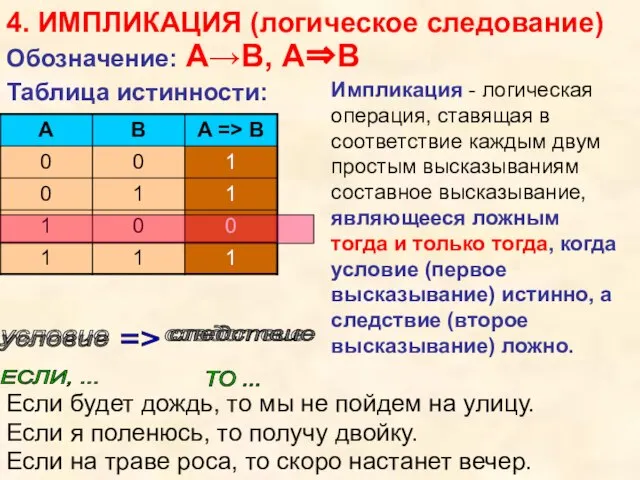
- 14. 4. ИМПЛИКАЦИЯ (логическое следование) условие следствие ЕСЛИ, ... ТО ... => условие следствие Если будет дождь,
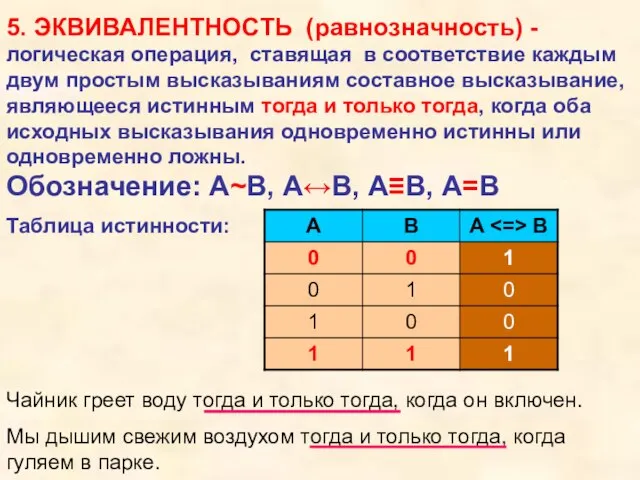
- 15. 5. ЭКВИВАЛЕНТНОСТЬ (равнозначность) - Чайник греет воду тогда и только тогда, когда он включен. Мы дышим
- 16. РЕШИМ ЗАДАЧИ: Определите, в каком порядке необходимо вычислять значение логического выражения: 1) ¬ А & ¬
- 17. Вычисление логических выражений Пример1. Вычислить значение логического выражения «(2·2=5 или 2·2=4}) и (2·2 ≠ 5 или
- 18. Задание 2. Определите истинность составного высказывания состоящего из простых высказываний: А={Принтер – устройство вывода информации} В={Процессор
- 19. Задание 3. Найти значения логического выражения: 1) 2) 3) 4) (0V1)→(1&1)= 1→1= 1 5) (1&1V0)↔(¬1&1)= 1↔0
- 20. ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ ПО ЛОГИЧЕСКОМУ ВЫРАЖЕНИЮ Таблицу, показывающую, какие значения принимает сложное высказывание при всех сочетаниях
- 21. Порядок действий: Количество строк в таблице Q=2n, где n - количество переменных (аргументов), здесь n =
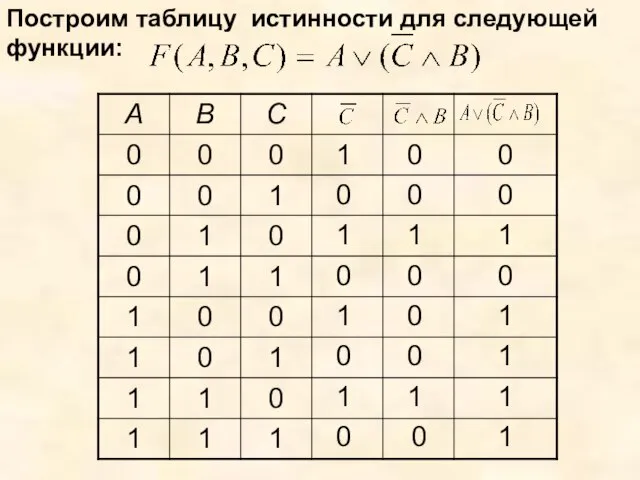
- 22. Построим таблицу истинности для следующей функции: 1 1 1 1 0 0 0 0 0 0
- 23. Задание. Построить таблицу истинности для следующих функций: 0 0 1 1 1 0 1 0 0
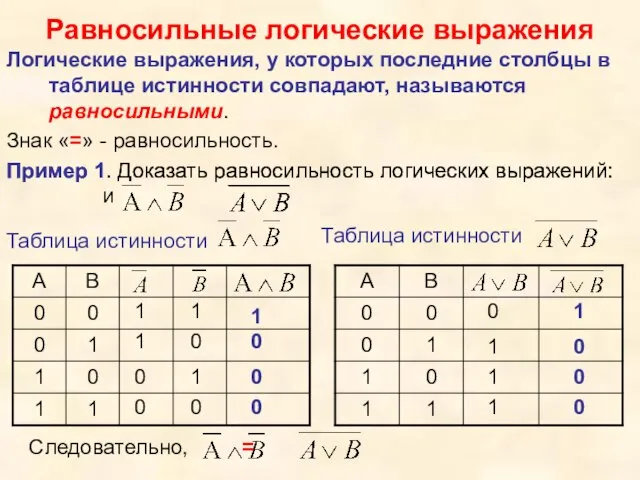
- 24. Пример 1. Доказать равносильность логических выражений: и Равносильные логические выражения Логические выражения, у которых последние столбцы
- 25. № 3.2. (Д.р.) Записать составное выражение «(2·2=4 и 3·3=9) или (2·2≠4 и 3·3≠9)» в форме логического
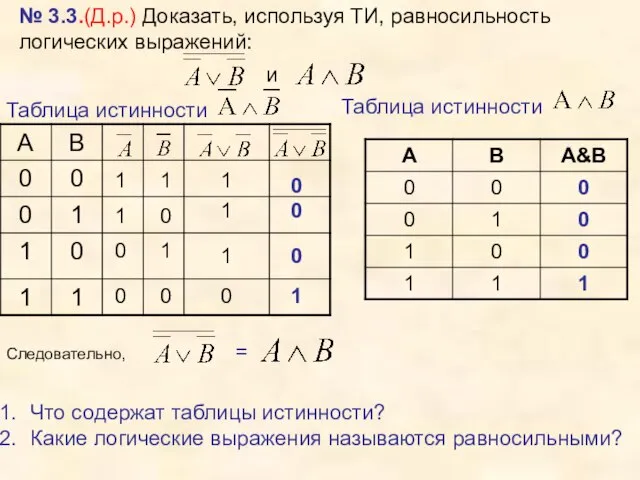
- 26. № 3.3.(Д.р.) Доказать, используя ТИ, равносильность логических выражений: 0 1 1 1 0 0 1 0
- 27. Логической (булевой) функцией называют функцию F(Х1, Х2, ..., Хn), аргументы которой Х1, Х2, ..., Хn (независимые
- 28. Пример 3.10. По имеющимся таблицам истинности выразите через базовые логические функции (конъюнкцию, дизъюнкцию и отрицание) следующие
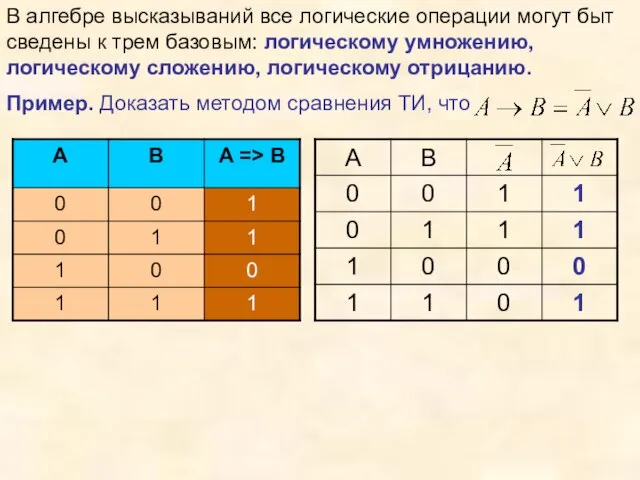
- 29. В алгебре высказываний все логические операции могут быт сведены к трем базовым: логическому умножению, логическому сложению,
- 30. № 3.4. Доказать, пользуясь ТИ, что операция эквивалентности равносильна выражению 1 0 1 0 1 0
- 31. Законы алгебры логики и свойства логических операций используются для упрощения логических выражений (минимизации логических функций)
- 33. Скачать презентацию






















 Программирование на языке Python. Области видимости переменных. Вложенные функции
Программирование на языке Python. Области видимости переменных. Вложенные функции Построение карты плотности Омской области в программе CorelDRAW
Построение карты плотности Омской области в программе CorelDRAW Операционные системы реального времени QNX и интегрированный комплект разработчика QNX Momentics
Операционные системы реального времени QNX и интегрированный комплект разработчика QNX Momentics Искусство эпохи Средневековья
Искусство эпохи Средневековья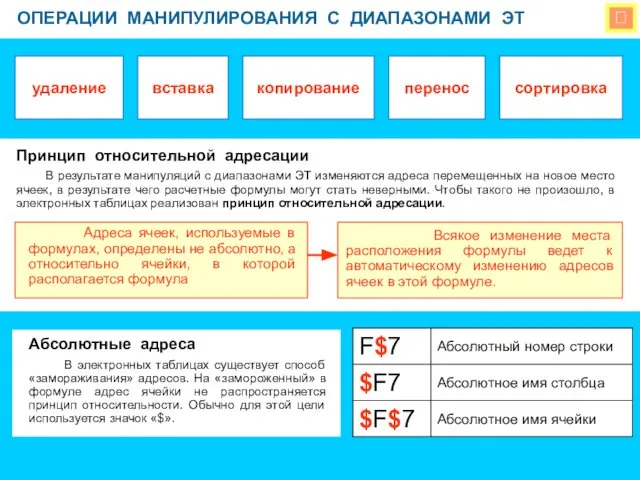 Операции манипулирования с диапазонами
Операции манипулирования с диапазонами Операционная система Windows
Операционная система Windows Потапова Ирина Александровна учитель информатики МОУ гимназии № 15 Советского района г.Волгограда
Потапова Ирина Александровна учитель информатики МОУ гимназии № 15 Советского района г.Волгограда Cоздание сцены в 3D studio max
Cоздание сцены в 3D studio max Блог Блог (англ. blog, от web log — Интернет-журнал событий, Интернет-дневник, онлайн-дневник) — веб-сайт, основное содержимое которого
Блог Блог (англ. blog, от web log — Интернет-журнал событий, Интернет-дневник, онлайн-дневник) — веб-сайт, основное содержимое которого  Симметричные криптосистемы. Лекция 1. Основные понятия и определения криптографии
Симметричные криптосистемы. Лекция 1. Основные понятия и определения криптографии Проектирование локальной вычислительной сети по технологии Ethernet на примере администрации
Проектирование локальной вычислительной сети по технологии Ethernet на примере администрации Языки программирования. Java: стоит ли его изучать?
Языки программирования. Java: стоит ли его изучать? Циклические алгоритмы. Реализация циклов в Object Pascal
Циклические алгоритмы. Реализация циклов в Object Pascal PowerPoint В этой презентации я продемонстрирую умения в использовании программой PowerPoint.
PowerPoint В этой презентации я продемонстрирую умения в использовании программой PowerPoint. Pastel Presentation Template (image not include)
Pastel Presentation Template (image not include) Презентация к теме 15 лит-ра для 78,79 групп
Презентация к теме 15 лит-ра для 78,79 групп Безопасный интернет. Сокровища и ловушки интернета
Безопасный интернет. Сокровища и ловушки интернета Понятие об информационных системах (ИС) и геоинформационных системах (ГИС)
Понятие об информационных системах (ИС) и геоинформационных системах (ГИС) Основы алгоритмизации и программирования
Основы алгоритмизации и программирования Автор: Кулаева Надежда Александровна Автор: Кулаева Надежда Александровна МОУ «Межениновская СОШ» Томской области Учитель инфо
Автор: Кулаева Надежда Александровна Автор: Кулаева Надежда Александровна МОУ «Межениновская СОШ» Томской области Учитель инфо Двумерные массивы Введение
Двумерные массивы Введение Оператор адреса (&)
Оператор адреса (&) Структура ГИС. Аналогово-цифровое преобразования данных
Структура ГИС. Аналогово-цифровое преобразования данных Базы данных в EXCEL
Базы данных в EXCEL Использование компьютерной сети
Использование компьютерной сети подготовила Силантьева Т.Г. учитель информатики МБОУ «СОШ №2 р.п. Базарный Карабулак Саратовской области»
подготовила Силантьева Т.Г. учитель информатики МБОУ «СОШ №2 р.п. Базарный Карабулак Саратовской области»  Презентация "Типовая корпоративная сеть, понятие уязвимости и атаки - 1" - скачать презентации по Информатике
Презентация "Типовая корпоративная сеть, понятие уязвимости и атаки - 1" - скачать презентации по Информатике Введение в Delphi. Главное окно: пиктографические кнопки, палитра
Введение в Delphi. Главное окно: пиктографические кнопки, палитра