Содержание
- 2. Постановка задачи о максимальном потоке Алгоритм Форда-Фалкерсона нахождения максимального потока Содержание
- 3. Транспортной сетью называют связный граф без циклов, в котором: существует единственная вершина s, из которой дуги
- 4. Потоком в сети ϕ называется целочисленная функция, заданная на дугах графа, такая, что: для любой дуги
- 5. Из этого же равенства и из того, что в сети нет контуров, следует, что суммарный поток,
- 6. Назовем дугу насыщенной, если для нее величина потока равна пропускной способности дуги: ϕij=сij. Путь между вершинами
- 7. Зададим на сети любой поток и доведем его до полного. Для этого перебираем все пути между
- 8. Разметка выделяет цепь между источником и стоком сети. Будем двигаться от стока к источнику и восстановим
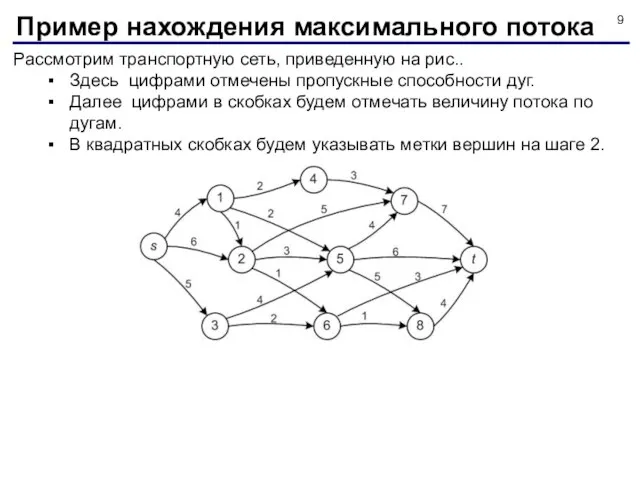
- 9. Рассмотрим транспортную сеть, приведенную на рис.. Здесь цифрами отмечены пропускные способности дуг. Далее цифрами в скобках
- 10. Выполним шаг 1 алгоритма. Зададим начальный поток по дугам по следующему правилу: выделим несколько путей, начинающихся
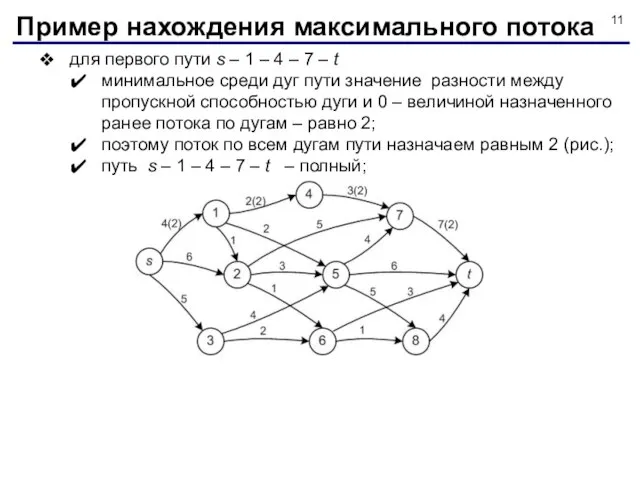
- 11. для первого пути s – 1 – 4 – 7 – t минимальное среди дуг пути
- 12. для второго пути s – 2 – 7 – t минимальное среди дуг пути значение разности
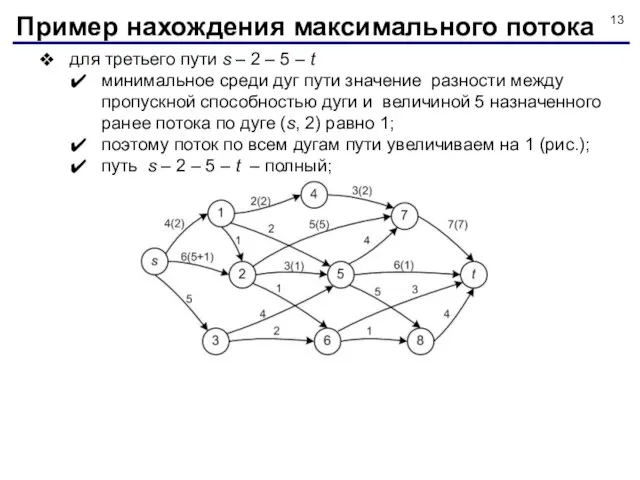
- 13. для третьего пути s – 2 – 5 – t минимальное среди дуг пути значение разности
- 14. для четвертого пути s – 3 – 6 – 8 – t минимальное среди дуг пути
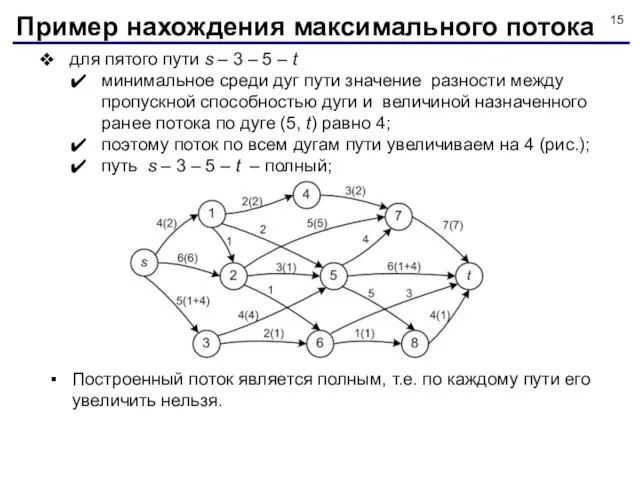
- 15. для пятого пути s – 3 – 5 – t минимальное среди дуг пути значение разности
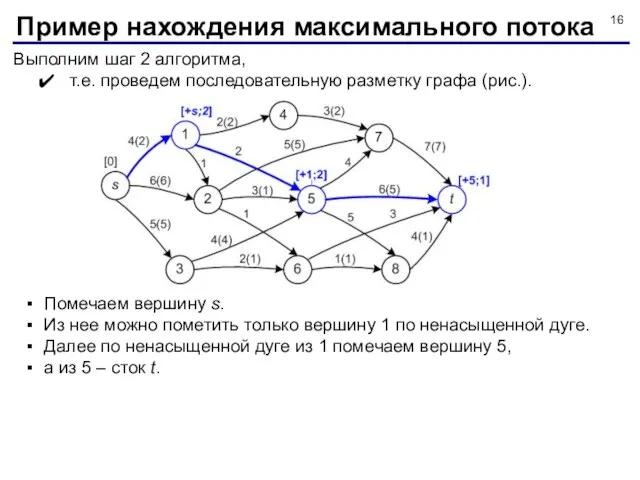
- 16. Выполним шаг 2 алгоритма, т.е. проведем последовательную разметку графа (рис.). Пример нахождения максимального потока Помечаем вершину
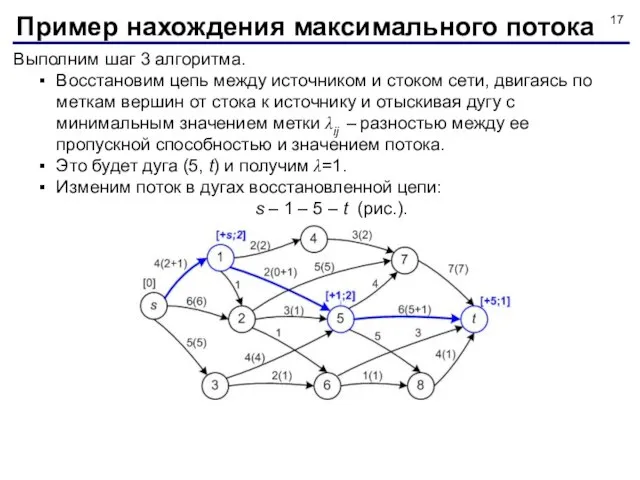
- 17. Выполним шаг 3 алгоритма. Восстановим цепь между источником и стоком сети, двигаясь по меткам вершин от
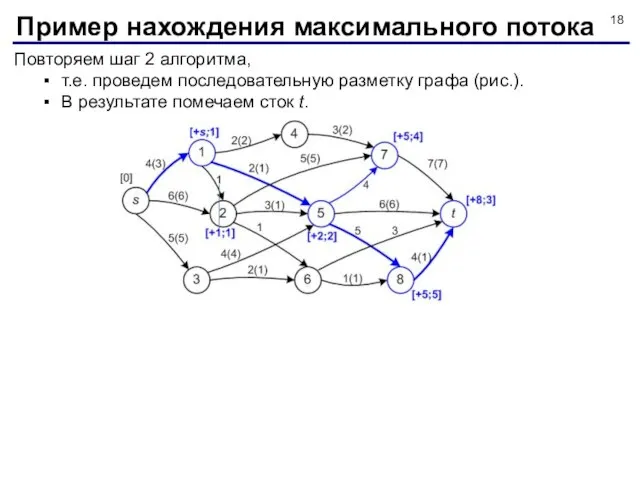
- 18. Повторяем шаг 2 алгоритма, т.е. проведем последовательную разметку графа (рис.). В результате помечаем сток t. Пример
- 19. Выполним шаг 3 алгоритма. Восстановим путь между источником и стоком сети. Получим путь s – 1
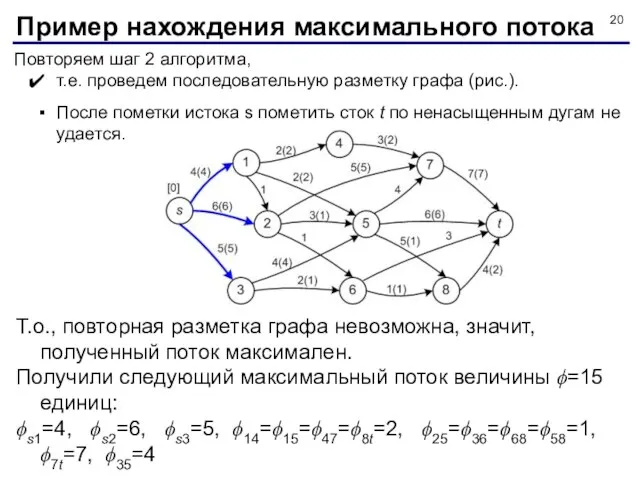
- 20. Повторяем шаг 2 алгоритма, т.е. проведем последовательную разметку графа (рис.). После пометки истока s пометить сток
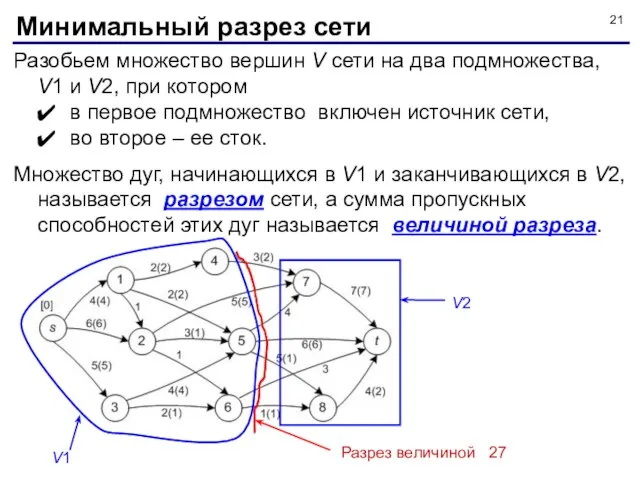
- 21. Разобьем множество вершин V сети на два подмножества, V1 и V2, при котором в первое подмножество
- 22. Разрез, величина которого минимальна, называется минимальным разрезом. Для проверки того, является ли поток максимальным, служит Теорема
- 24. Скачать презентацию












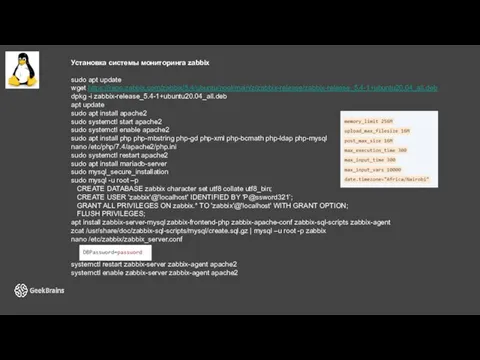 Установка системы мониторинга zabbix
Установка системы мониторинга zabbix Информатика до нашей эры
Информатика до нашей эры Локализация сайтов на примере Kaspersky Online Help
Локализация сайтов на примере Kaspersky Online Help Криптография с открытым ключом
Криптография с открытым ключом Презентация "Современные системы программирования" - скачать презентации по Информатике
Презентация "Современные системы программирования" - скачать презентации по Информатике Эксплуатационная документация
Эксплуатационная документация Система управления памятью в персональной ЭВМ
Система управления памятью в персональной ЭВМ Cerca una sveglia, i forbici, una teiera
Cerca una sveglia, i forbici, una teiera Информация и информационные процессы
Информация и информационные процессы Интерактивные тесты в Microsoft Office Excel
Интерактивные тесты в Microsoft Office Excel Организация ввода-вывода из файлов
Организация ввода-вывода из файлов Прогнозирование в Deductor. Задача прогнозирования
Прогнозирование в Deductor. Задача прогнозирования Среда программирования С++
Среда программирования С++ Си тілінде массив элементтерін енгізу және шығару
Си тілінде массив элементтерін енгізу және шығару Для чего нужна вода Окружающий мир 2 класс
Для чего нужна вода Окружающий мир 2 класс  Проставление статусов в личном кабинете агента Ефин
Проставление статусов в личном кабинете агента Ефин Владивостокский государственный университет экономики и сервиса Институт информатики, инноваций и бизнес систем Кафедра инфо
Владивостокский государственный университет экономики и сервиса Институт информатики, инноваций и бизнес систем Кафедра инфо Теоретические основы языков манипулирования данными
Теоретические основы языков манипулирования данными Программирование. Базовый курс 2 часть
Программирование. Базовый курс 2 часть Презентация "Архитектура ПК" - скачать презентации по Информатике
Презентация "Архитектура ПК" - скачать презентации по Информатике Работа с документами в программе MS Word
Работа с документами в программе MS Word Реляционная модель данных
Реляционная модель данных Разработка приложений на платформе .NET
Разработка приложений на платформе .NET Презентация "Подготовка к контрольной работе" - скачать презентации по Информатике
Презентация "Подготовка к контрольной работе" - скачать презентации по Информатике Типы полей в реляционных базах данных
Типы полей в реляционных базах данных Освоение технологии работы в графическом редакторе
Освоение технологии работы в графическом редакторе Моделирование информационного обеспечения. Моделирование данных
Моделирование информационного обеспечения. Моделирование данных Презентация "АРХИТЕКТУРА КОМПЬЮТЕРА" - скачать презентации по Информатике
Презентация "АРХИТЕКТУРА КОМПЬЮТЕРА" - скачать презентации по Информатике