Содержание
- 2. ПРЕДМЕТ, МЕТОД И ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДОВ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Вопросы: 1.1. Понятие и теоретические основы методов линейного
- 3. Интерес к фактическому применению МП возрос с 1947 г., когда крупный американский математик Дж. Данциг разработал
- 4. В сельскохозяйственном производстве круг задач очень широк. Многие известные отечественные и зарубежные математики и экономисты, специализирующиеся
- 5. Например, любой бухгалтерский или плановый баланс, состоящий, как известно, из двух частей: источников поступления средств и
- 6. Если мы разложим итоговую приходную и расходную части на их составляющие, то соотношения, естественно, не изменяются.
- 7. Пусть X1 обозначает запасы на начало года; Х2 – производство; Х3 – приобретение со стороны; Y1
- 8. Аналогичным образом можно составить и записать соотношения по всем остальным производственно-финансовым балансам. Если обозначить все позиции
- 9. Допустим, нам необходимо составить производственно-финансовый план хозяйства, причем такой, чтобы в результате его практической реализации хозяйство
- 10. Обозначим через Х1, Х2, ..., Хn множество неизвестных величин производственно-финансового плана, подлежащих определению, а через m
- 11. Поскольку на производство какого-либо продукта всегда затрачиваются некоторые ресурсы, то необходимо ввести общее обозначение для нормативов
- 13. Экономически условия, записанные в виде системы, интерпретируются так: затраты любого из m видов ресурса на производство
- 14. Целевая установка данной задачи – достижение максимальной прибыли. Если допустить, что единица первого продукта приносит некоторую
- 15. Условия задачи, объединенные вместе, характеризуют поставленную задачу в ее математической форме. В задачах линейного программирования все
- 16. Например, неравенство вида 0,07X1+0,05X2 в задаче характеризует тот факт, что площадь под просо и гречиху не
- 17. Поскольку в задачах линейного программирования отыскивается оптимальное решение, то в них необходимо кроме условий (ограничений) задачи
- 18. Технико-экономические коэффициенты – это есть соответствующие нормативы, т. е. те числовые коэффициенты, которые вводятся в левые
- 19. Общая задача линейного программирования Заданы: линейная функция Z = C1X1 + C2X2 + . . .
- 21. Определение 1. Задача, в которой требуется найти такие неотрицательные значения Х1, Х2, ..., Хn, которые удовлетворяют
- 22. Определение 3. Задача с условиями вида: Z =СХ max, AX =0 называется симметричной задачей линейного программирования.
- 23. Определение 5. Набор чисел X=(X1, Х2, …, Хn), удовлетворяющих ограничениям задачи линейного программирования, называется ее планом.
- 24. Геометрическая интерпретация и графический способ решения простейших задач линейного программирования. Применяется в основном при решении задач
- 25. Задача. При анализе перспективного плана развития хозяйства обнаружилось, что в нем недоиспользуется 200 га пашни. Наиболее
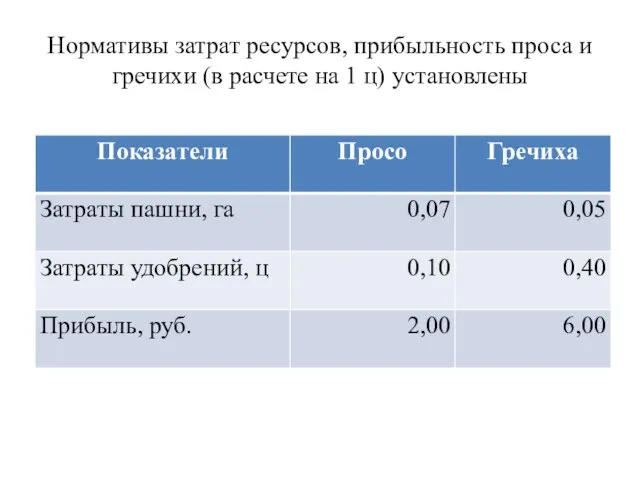
- 26. Нормативы затрат ресурсов, прибыльность проса и гречихи (в расчете на 1 ц) установлены
- 27. Обозначим через X1 – объем производства проса (ц), через Х2 объем производства гречихи (ц), запишем условия
- 29. Рассмотрим первое неравенство: 0,07X1+0,05X2 Разрешим его относительно Х2 (можно и относительно X1); знак Итак, если X1=1000,
- 30. Если свободный член 200 этого уравнения сокращать в соответствии с условием задачи, то линии, параллельные 1,
- 31. Прямая k, соответствующую второму неравенству: 0,1Х1+0,4Х2 = 800; X1 + 4X2 =8000; X1 = 8000 –
- 32. Поскольку третье неравенство отражает ограниченность объема производства гречихи (Х2>=1000) снизу (не менее 1000 ц), то строим
- 33. Построив линии, соответствующие уравнениям задачи, и определив направление движения семейства параллельных прямых в соответствии с изменением
- 34. Рассматривая график, видим, что точке G соответствуют значения X1 1700, Х2 1600. Итак, максимальная величина прибыли
- 35. При необходимости координаты точки G можно определить точно. Для этого надо решить систему двух уравнений, каждое
- 36. Легко убедиться, что именно в этом случае, то есть при X1=1740 и Х2=1565, прибыль будет максимальной.
- 38. Скачать презентацию










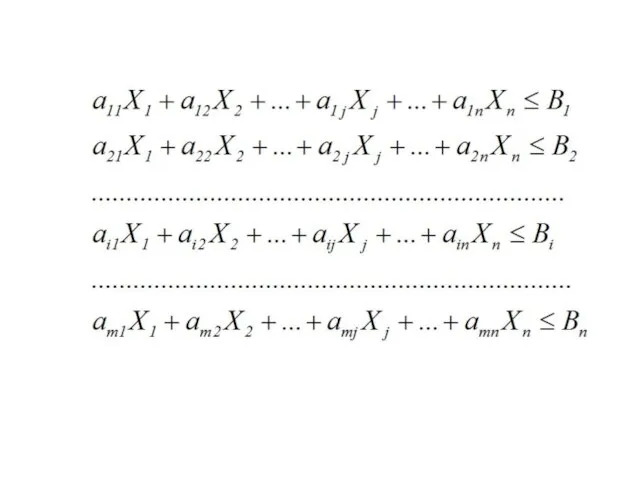























 Функции в Python
Функции в Python Методы и средства защиты информации от несанкционированного доступа
Методы и средства защиты информации от несанкционированного доступа Построение графиков функций в табличном редакторе MS EXCEL
Построение графиков функций в табличном редакторе MS EXCEL Параллельное программирование в стандарте MPI
Параллельное программирование в стандарте MPI Возможности сетевого программного обеспечения для организации коллективной деятельности в глобальных
Возможности сетевого программного обеспечения для организации коллективной деятельности в глобальных Создание объектов в 3d max. Задание 2
Создание объектов в 3d max. Задание 2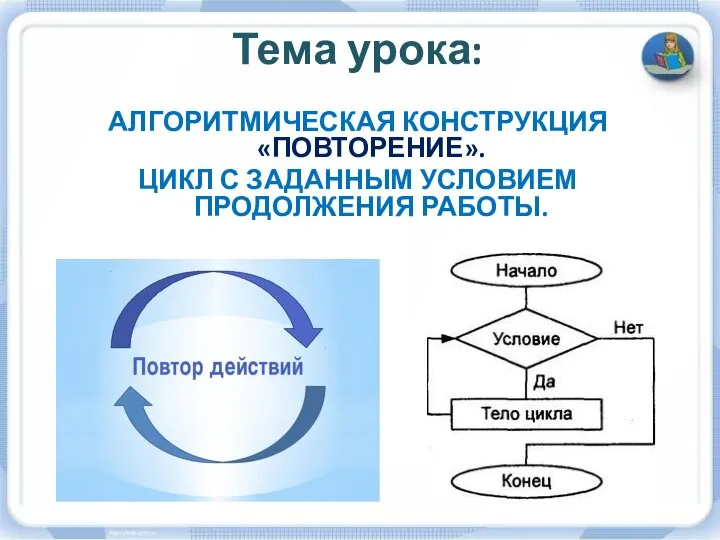 «Повторение» и почему его называют циклом?
«Повторение» и почему его называют циклом? Компьютерные вирусы и антивирусные программы
Компьютерные вирусы и антивирусные программы Презентация "Понятие «информация» и свойства информации" - скачать презентации по Информатике
Презентация "Понятие «информация» и свойства информации" - скачать презентации по Информатике Основы объектно-ориентированного программирования. (Лабораторная работа 1)
Основы объектно-ориентированного программирования. (Лабораторная работа 1) Методология и методика медиа-исследований
Методология и методика медиа-исследований Библиотек@: создай свое будущее. Библиотека села Великий Суходол
Библиотек@: создай свое будущее. Библиотека села Великий Суходол SMS – язык. Оксфордский словарь
SMS – язык. Оксфордский словарь Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную и обратно
Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную и обратно Безопасность в интернете Выполнила учитель информатики и ИКТ Стасева М.С.
Безопасность в интернете Выполнила учитель информатики и ИКТ Стасева М.С. Fix WIFI Mac Address instruction
Fix WIFI Mac Address instruction Средства пакета Microsoft Office. PowerPoint
Средства пакета Microsoft Office. PowerPoint Устройство обработки информации Процессор
Устройство обработки информации Процессор Эффективные алгоритмы сортировки
Эффективные алгоритмы сортировки Информационное обеспечение государственного управления
Информационное обеспечение государственного управления WR02C MiNi Wireless Router Specification
WR02C MiNi Wireless Router Specification ИТ-сервис – основа деятельности современной ИС службы
ИТ-сервис – основа деятельности современной ИС службы Microsoft Excel программасының функциясы
Microsoft Excel программасының функциясы Интернет-Олимпиады по программированию подготовила Савина Елена Геннадьевна, учитель МОУ « Березовская СОШ» П Канифольный, Ни
Интернет-Олимпиады по программированию подготовила Савина Елена Геннадьевна, учитель МОУ « Березовская СОШ» П Канифольный, Ни Організація баз даних та знань. Моделі даних. Ієрархічна та мережна модель даних
Організація баз даних та знань. Моделі даних. Ієрархічна та мережна модель даних Підготовка текстового документа до друку. Друк текстового документа
Підготовка текстового документа до друку. Друк текстового документа Типичные нарушения законодательства о защите прав потребителей и рекламе при осуществлении интернет-торговли
Типичные нарушения законодательства о защите прав потребителей и рекламе при осуществлении интернет-торговли Вопросы на смекалку
Вопросы на смекалку