Содержание
- 2. Раздел 5. Бездеформационные моды колебаний БЕЗДЕФОРМАЦИОННЫЕ МОДЫ И ВЕКТОРЫ. АСПЕКТЫ ТЕОРИИ……………… 5 - 3 ВЫЧИСЛЕНИЕ БЕЗДЕФОРМАЦИОННЫХ
- 3. Бездеформационные моды и векторы. Аспекты теории Незакрепленная конструкция может перемещаться без возникновения в ней внутренних сил
- 4. Бездеформационные моды и векторы. Аспекты теории Присутствие жестких тел и/или механизмов обнаруживается по наличию нулевых собственных
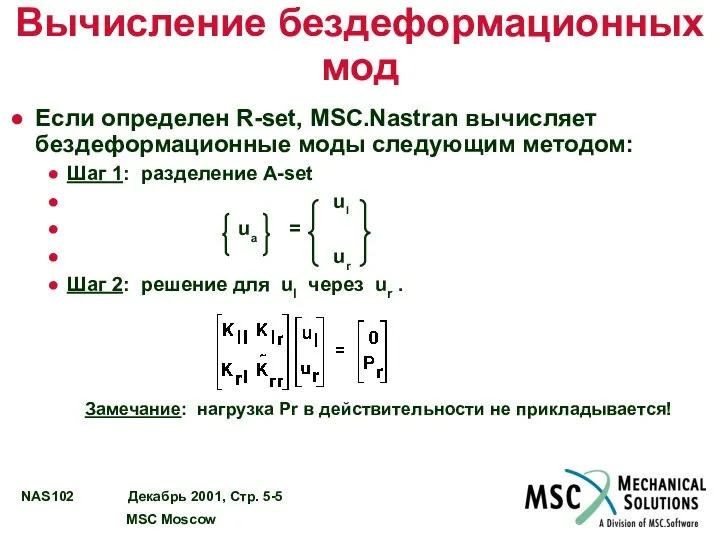
- 5. Вычисление бездеформационных мод Если определен R-set, MSC.Nastran вычисляет бездеформационные моды следующим методом: Шаг 1: разделение A-set
- 6. Вычисление бездеформационных мод ul = Dm ur где Это используется для формирования совокупности бездеформационных мод.
- 7. Вычисление бездеформационных мод Шаг 3: Преобразования матриц где [Mr] – в общем случае недиагональная матрица Методом
- 8. Выбор степеней свободы для оператора SUPORT Выбор степеней свободы для оператора SUPORT нужно производить с осторожностью.
- 9. Проверка степеней свободы, указанных в операторе SUPORT MSC.Nastran вычисляет энергию деформаций (работу) для каждой бездеформационной моды.
- 10. Проверка степеней свободы, указанных в операторе SUPORT Если не принимать во внимание ошибки округления, коэффициент погрешности
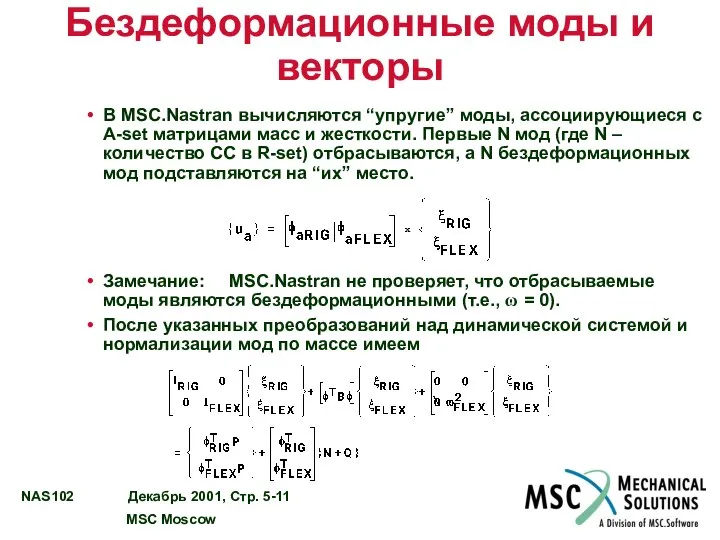
- 11. Бездеформационные моды и векторы В MSC.Nastran вычисляются “упругие” моды, ассоциирующиеся с A-set матрицами масс и жесткости.
- 12. Бездеформационные моды и векторы В результате преобразований имеем: Усилия закреплений отсутствуют, т.е. Если элементы демпфирования не
- 13. Бездеформационные моды и векторы Если демпфирование “пропорциональное”, тогда Уравнения динамики при модальном анализе полностью несвязанные.
- 15. Скачать презентацию




![Вычисление бездеформационных мод Шаг 3: Преобразования матриц где [Mr] – в](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1278573/slide-6.jpg)





 Тема урока: «Моделирование, как метод познания» Автор: Кондратенко Наталья Дмитриевна Место работы: МОУ СОШ № 19 г. Славянска-на-К
Тема урока: «Моделирование, как метод познания» Автор: Кондратенко Наталья Дмитриевна Место работы: МОУ СОШ № 19 г. Славянска-на-К Типы компьютеров Основные характеристики и области использования
Типы компьютеров Основные характеристики и области использования Информационная безопасность
Информационная безопасность Технология хранения, поиска и сортировки информации. Работу выполнили ученики 11 класса: Черных Елена и Навезнев Алексей.
Технология хранения, поиска и сортировки информации. Работу выполнили ученики 11 класса: Черных Елена и Навезнев Алексей. Медицинские базы данных
Медицинские базы данных Дети вне интернет-зависимости
Дети вне интернет-зависимости Организация документооборота. Информационно-поисковые справочники
Организация документооборота. Информационно-поисковые справочники Безопасное и рациональное использование личных и персональных данных в интернет-пространстве. Занятие 7
Безопасное и рациональное использование личных и персональных данных в интернет-пространстве. Занятие 7 Виды информации по способу восприятия
Виды информации по способу восприятия Автор: Фадеева Елена Аркадьевна
Автор: Фадеева Елена Аркадьевна Викторина по информатике «Инфознайка» Учитель информатики МКОУ Светлоярской СОШ №2 им.Ф Ф Плужникова Скворцова Ирина Ник
Викторина по информатике «Инфознайка» Учитель информатики МКОУ Светлоярской СОШ №2 им.Ф Ф Плужникова Скворцова Ирина Ник Базы данных. Типы данных. Ограничения целостности
Базы данных. Типы данных. Ограничения целостности Определение понятия. Видовое понятие. Родовое понятие. Видовое отличие
Определение понятия. Видовое понятие. Родовое понятие. Видовое отличие Информационная безопасность. Методы защиты информации
Информационная безопасность. Методы защиты информации Основы Python. Пакет NumPy
Основы Python. Пакет NumPy Съёмные носители информации. 5 класс
Съёмные носители информации. 5 класс Системы счисления. Двоичное кодирование в компьютере
Системы счисления. Двоичное кодирование в компьютере Реляционная модель данных
Реляционная модель данных Требования к оформлению презентации к защите курсовой работы
Требования к оформлению презентации к защите курсовой работы Примеры комплектации компьютерного рабочего места в соответствии с целями его использования для направлений деятельности
Примеры комплектации компьютерного рабочего места в соответствии с целями его использования для направлений деятельности Создание кроссворда в текстовом процессоре Word. 8 класс
Создание кроссворда в текстовом процессоре Word. 8 класс Структури. Описання шаблона структури
Структури. Описання шаблона структури Аттестационная работа. Методическая разработка исследовательского урока Знакомство с клавиатурой
Аттестационная работа. Методическая разработка исследовательского урока Знакомство с клавиатурой Вычислительные системы, сети и телекоммуникации
Вычислительные системы, сети и телекоммуникации Buying a computer
Buying a computer Проектирование программных систем
Проектирование программных систем ТАБЛИЧНЫЕ ИНФОРМАЦИОННЫЕ МОДЕЛИ
ТАБЛИЧНЫЕ ИНФОРМАЦИОННЫЕ МОДЕЛИ Автоматическая генерация интерфейса пользователя по бизнес модели
Автоматическая генерация интерфейса пользователя по бизнес модели