Сбалансированные поисковые деревья АВЛ-дерево

Словарные операции

поиск элемента с заданным ключом х
добавление нового элемента с заданным

поиск элемента с заданным ключом х

произвольный массив
O(n)

ФПМИ БГУ

упорядоченный массив
O(log n)

поисковое дерево

добавление элемента с заданным ключом х

ФПМИ БГУ

произвольный массив
O(1)

упорядоченный массив
O(n)

поисковое дерево
O(h),

удаление элемента с заданным ключом х

ФПМИ БГУ

произвольный массив
O(n)

упорядоченный массив
O(n)

поисковое дерево
O(h)
если

Сбалансированные деревья

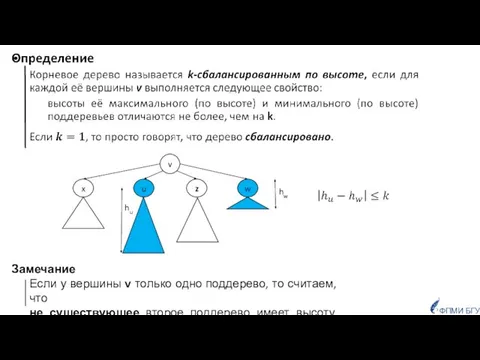
ФПМИ БГУ

Замечание
Если у вершины v только одно поддерево, то считаем,

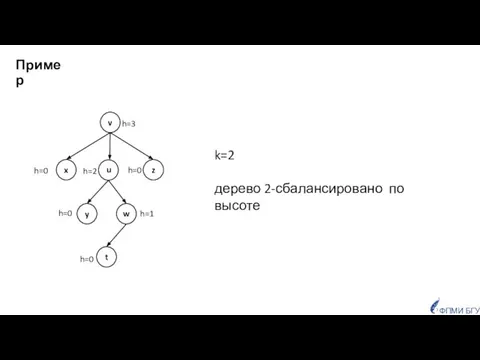
Пример

h=3

h=0

h=0

h=0

h=1

h=2

h=0

k=2
дерево 2-сбалансировано по высоте

ФПМИ БГУ

v

x

z

y

t

w

u

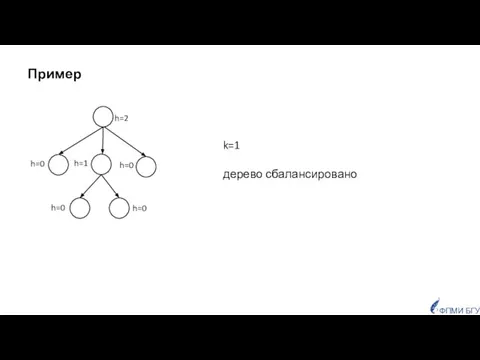
h=0

k=1
дерево сбалансировано

ФПМИ БГУ

h=2

h=0

h=0

h=1

h=0

Пример

Высота полного бинарного дерева h=O(log n), где n – количество вершин.

ФПМИ

Идеально сбалансированные деревья

ФПМИ БГУ

ФПМИ БГУ

Замечание
Если у вершины v только одно поддерево, то считаем,

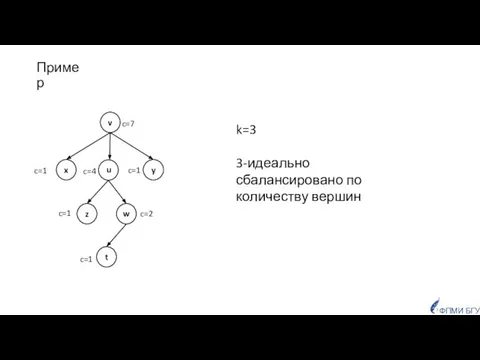
Пример

k=3
3-идеально сбалансировано по количеству вершин

ФПМИ БГУ

c=7

c=1

c=1

c=1

c=2

c=4

c=1

v

x

y

z

t

w

u

ФПМИ БГУ

Каждое идеально-сбалансированное дерево является сбалансированным. Обратное верно не всегда.

Дерево на

Оценки для бинарных поисковых деревьев

10

18

19

6

2

построение дерева для последовательности из n

ФПМИ БГУ

В 1962 году советские учёные
Г.М.Адельсон-Вельский
и 
Е.М.Ландис
предложили структуру данных сбалансированного

Георгий Максимович Адельсон-Вельский

Евгений Михайлович Ландис 

АВЛ-дерево – это бинарное поисковое дерево, которое является сблансированным по высоте.

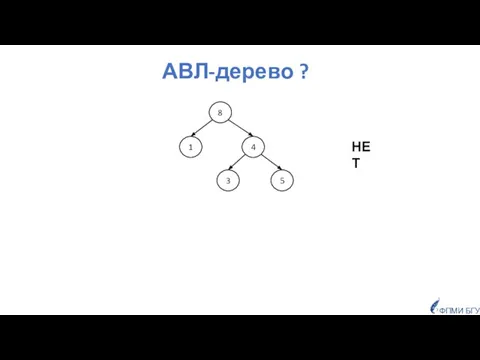
АВЛ-дерево ?
Нет, так как оно не поисковое.

8

4

1

3

5

ФПМИ БГУ

НЕТ

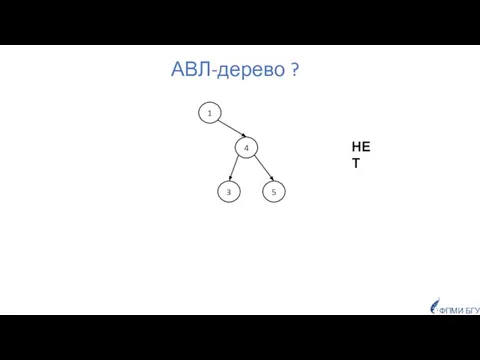
АВЛ-дерево ?

1

4

3

5

ФПМИ БГУ

НЕТ

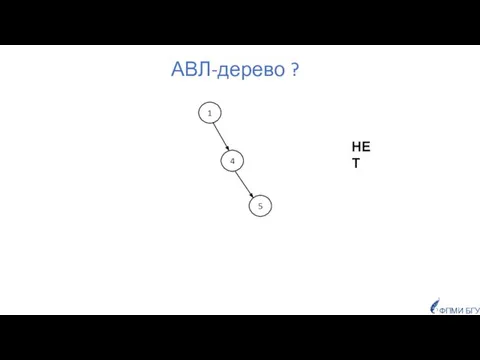
АВЛ-дерево ?

1

4

5

ФПМИ БГУ

НЕТ

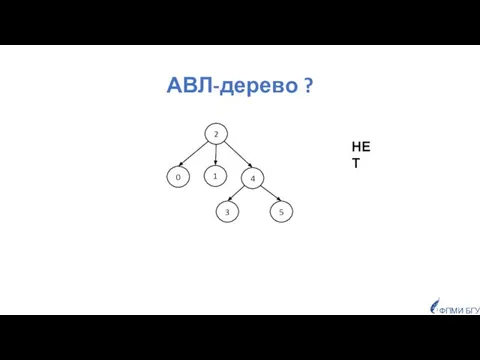
АВЛ-дерево ?

2

4

3

5

0

1

ФПМИ БГУ

НЕТ

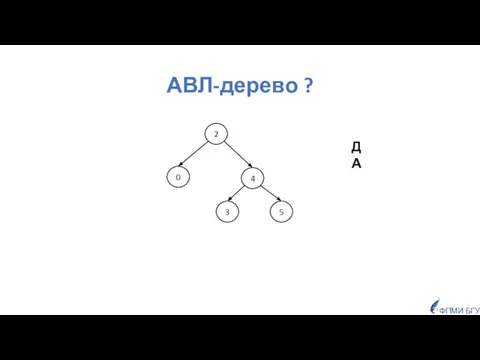
АВЛ-дерево ?

2

4

3

5

0

ФПМИ БГУ

ДА

ТЕОРЕМА
Пусть n – число внутренних вершин АВЛ-дерева, h – его высота.

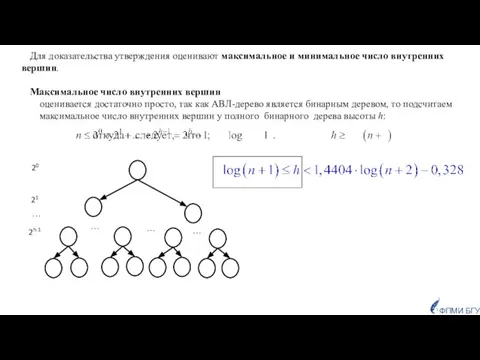
Для доказательства утверждения оценивают максимальное и минимальное число внутренних вершин.
Максимальное

Для оценки минимального числа внутренних вершин используются свойства чисел Фибоначчи.
Пусть

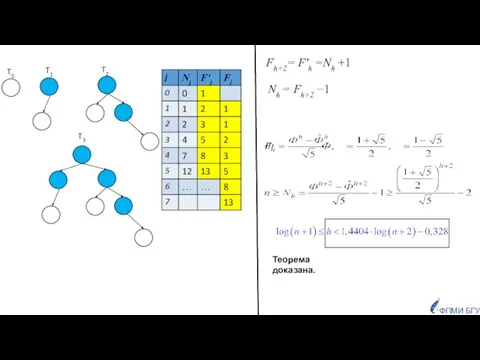
ФПМИ БГУ

T0

T1

T2

T3

Fh+2= F'h =Nh +1

Теорема доказана.

Nh = Fh+2 −1

ФПМИ БГУ

Операции поиска, добавления и удаления элементов для АВЛ-деревьев осуществляются точно

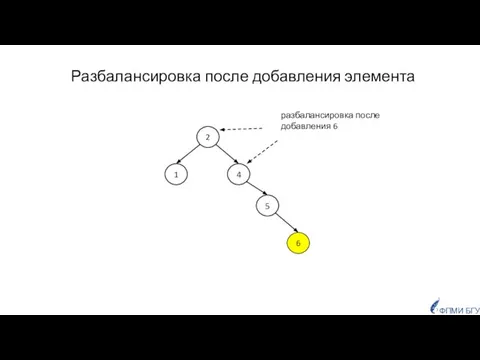
Разбалансировка после добавления элемента

2

4

1

5

6

разбалансировка после добавления 6

ФПМИ БГУ

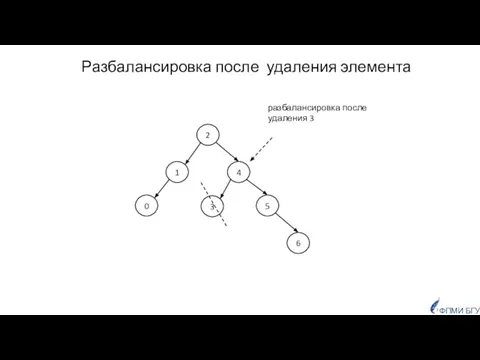
Разбалансировка после удаления элемента

2

4

1

5

6

разбалансировка после удаления 3

3

0

ФПМИ БГУ

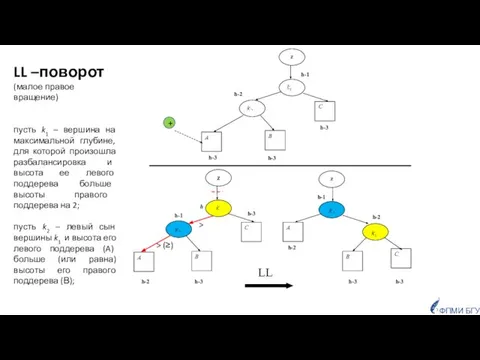
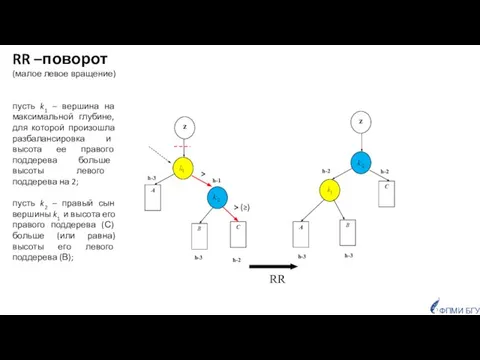
Балансировки

LL поворот (малое правое вращение, одинарный правый поворот)
RR поворот (малое левое

h-1

h-3

h-1

h

z

C

A

B

z

B

A

C

h-2

h-3

h-3

h-3

h-2

h-2

LL

z

C

B

h-3

A

h-3

h-2

h-3

h-1

+

>

> (≥)

ФПМИ БГУ

LL –поворот
(малое правое вращение)
пусть k1 – вершина на максимальной

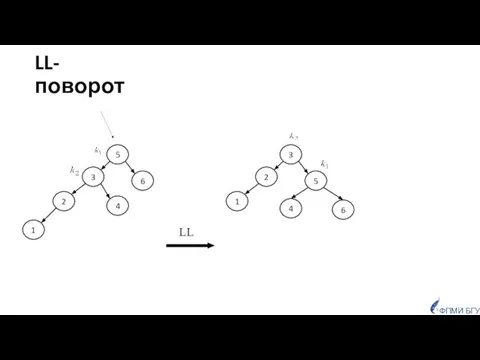
LL-поворот

5

3
6

2

4

3

2
5

1

4

6

ФПМИ БГУ

1

LL

RR

h-3

h-1

h-2

h-2

z

C

A

B

z

B

A

C

h-3

h-3

h-2

h-3

>

> (≥)

ФПМИ БГУ

RR –поворот
(малое левое вращение)
пусть k1 – вершина на максимальной

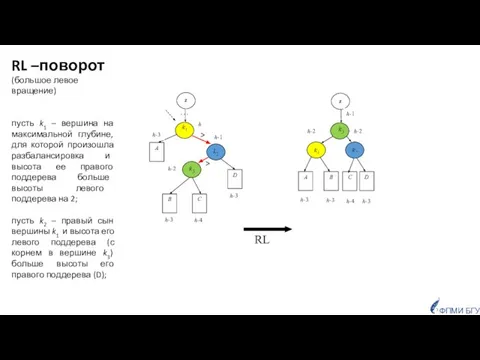
z

C

A

B

z

B

A

D

C

D

h-2

h-3

h-4

h-3

h-1

h-3

h

h-4

h-3

h-3

h-3

h-2

h-2

h-1

>

>

ФПМИ БГУ

RL –поворот
(большое левое вращение)
пусть k1 – вершина на максимальной глубине,

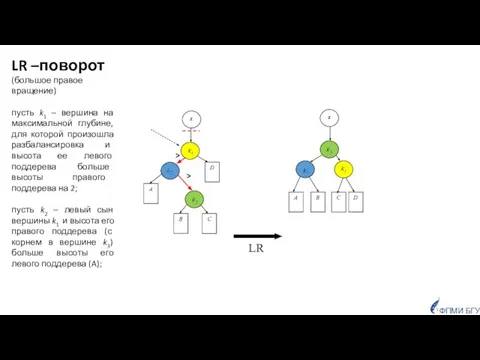
z

C

A

B

z

B

D

A

D

C

>

>

ФПМИ БГУ

LR –поворот
(большое правое вращение)
пусть k1 – вершина на максимальной глубине,

ОЦЕНКИ

Каждый из поворотов (LL, RR, LR, RL) выполняется за O(1), если

ФПМИ БГУ

После выполнения операции добавления элемента разбалансировка может произойти сразу у

ФПМИ БГУ

Процедура добавления элемента:
поиск отца для вершины x ;
добавление вершины x;
поиск

При удалении элемента x разбалансировка может произойти только у одной вершины:
найдём

ПРИМЕР

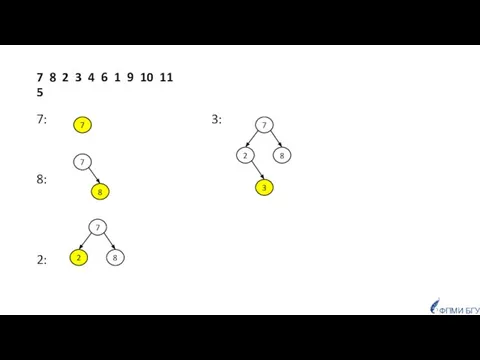
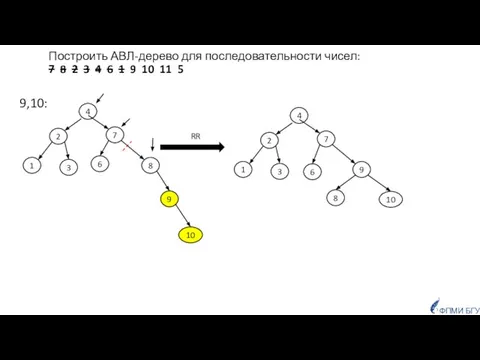
Построить АВЛ-дерево для последовательности чисел:
7, 8, 2, 3, 4, 6, 1,

7 8 2 3 4 6 1 9 10 11 5

7:

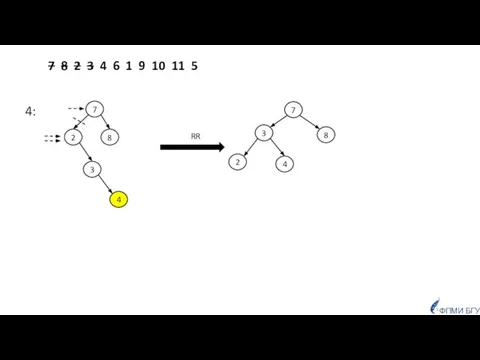
7 8 2 3 4 6 1 9 10 11 5

4:

7

8

2

3

4

RR

7

3

8

2

4

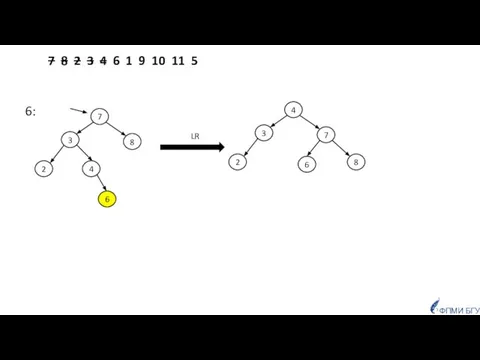
ФПМИ

7 8 2 3 4 6 1 9 10 11 5

6:

LR

7

3

8

2

4

4

3

7

2

6

6

8

ФПМИ

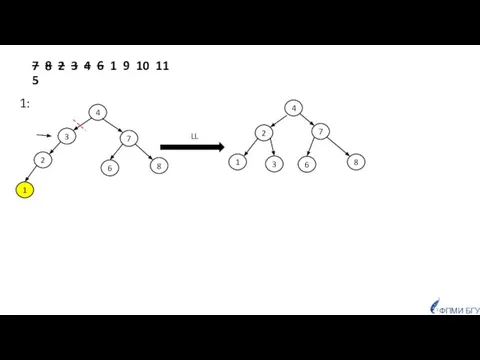
7 8 2 3 4 6 1 9 10 11 5

1:

LL

2

7

1

6

8

7

6

8

3

4

2

1

3

ФПМИ

Построить АВЛ-дерево для последовательности чисел: 7 8 2 3 4 6 1

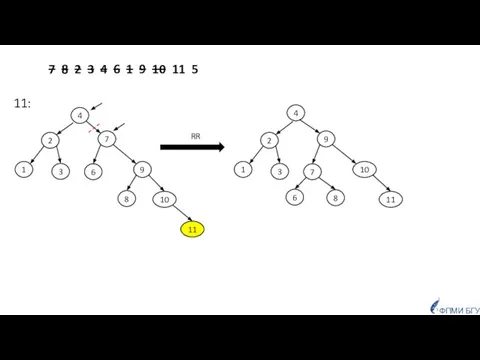
7 8 2 3 4 6 1 9 10 11 5

11:

RR

2

9

1

7

10

4

3

8

11

2

7

1

6

9

4

3

8

10

11

6

ФПМИ

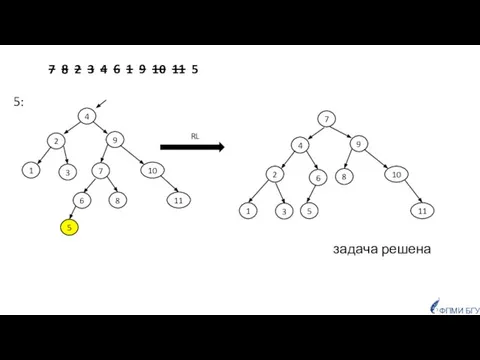
7 8 2 3 4 6 1 9 10 11 5

5:
задача

7, 8, 2, 3, 4, 6, 1, 9, 10, 11, 5

4

9

2

8

10

7

6

1

11

5

3

ФПМИ

Сортировка деревом

Предположим, что на вход поступаю числа, среди которых нет повторяющихся.

Абстрактный тип данных: множество (set)

Множество (англ. set) —хранит набор попарно различных

Абстрактный тип данных ассоциативный массив (map)

Ассоциативный массив (англ. associative array), или