Содержание
- 2. Цель: рассмотреть основные понятия числовых систем; правила построения систем; выполнение действий в системах счисления.
- 3. Алфавит Х из р символов и правила записи (изображения) и обработки чисел с помощью символов этого
- 4. Система счисления Любая система счисления – это система кодирования числовых величин (количеств), позволяющая выполнять операции кодирования
- 5. Основные понятия кодирования и шифрования Все системы счисления строятся по общему принципу: определяется величина р –
- 6. Позиционные и непозиционные системы счисления Система счисления в которой вес цифры (или символа алфавита) зависит от
- 7. Процедура перевода десятичных чисел в р-ную систему счисления: перевести отдельно целую часть числа х: последовательно делить
- 8. Пример: найти: 12,810 = ?2 Переводим целую часть: 1210 =11002; переводим дробную часть (выделены цифры, идущие
- 9. Примеры Найдем 29,2510 = ?8 . Решение имеет вид 1) 2910 = 358 ; 2) 0,2510
- 10. Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной
- 11. Переводы в смешанных системах Из 2-ной системы в 8-ную (двоично-восьмеричное изображение): из 8-ной системы в 2–ную
- 12. Переводы в смешанных системах из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение): из 16-ной системы в 2-ную
- 13. Арифметические операции: Сложение в двоичной системе счисления осуществляется по правилам 0 + 0 = 0, 0
- 14. Как представляются целые числа? Обычно занимают в памяти компьютера один или два байта. В однобайтовом формате
- 15. Примеры: а) число 7210 = 10010002 в однобайтовом формате: б) это же число в двубайтовом формате:
- 16. Целые числа со знаком Обычно занимают в памяти компьютера один, два или четыре байта, при этом
- 17. Прямой, обратный и дополнительный код. Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата,
- 18. Прямой, обратный и дополнительный код. Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
- 19. 2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули
- 20. Прямой, обратный и дополнительный код. Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в
- 21. Сложение обратных кодов. Здесь при сложении чисел А и В имеют место четыре основных и два
- 22. 2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Получен правильный результат в
- 23. 4. А и В отрицательные. Полученный первоначально неправильный результат (обратный код числа -1110 вместо обратного кода
- 24. 5. А и В положительные, сумма А+В больше, либо равна 2n-1, где n — количество разрядов
- 25. 6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна 2n-1. Здесь
- 26. Сложение дополнительных кодов. Здесь также имеют место рассмотренные выше шесть случаев: 1. А и В положительные.
- 27. 3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Получен правильный результат. Единицу
- 28. Обратный и дополнительный код Обратным кодом числа в системе с основанием р называется число в этой
- 29. Точность Точность в чистой математике – понятие абстрактное и в вычислительной математике может возникать иллюзия точности
- 30. Точность Так как диапазон n-разрядных чисел системы счисления с основанием p находится в пределах , то
- 31. В 1937 году Конрадом Цузе для увеличения диапазона чисел, представимых в арифметике двоичных чисел, а также
- 32. Пример: Пусть даны два числа: ( ). Тогда можно проверить, что результаты выполнения операций будут равны:
- 33. Если из n разрядов, отводимых под изображение чисел, m двоичных разрядов отвести под мантиссу, k –
- 34. Пример: Рассмотрим представление R с 3-разрядной мантиссой со знаком в диапазоне 0,1≤ | f | Диапазон
- 35. Числа, меньшие нижней границы положительных чисел и большие верхней границы отрицательных чисел, считаются равными нулю, не
- 36. Такое представление очень удобно для хранения в ЭВМ, так как на самом деле необходимо хранить не
- 37. -10^99 -10^(-100) 0 10^(-100) 10^(99) Отрицательное переполнение (1) Положительное переполнение (7) Выражаемые отрицательные числа (2) Выражаемые
- 38. К "неудобствам" этой формы представления чисел можно отнести возможность возникновения следующих "особо опасных" ситуаций: если число
- 39. может возникнуть так называемая ситуация "переполнения порядка" при сложении (умножении) очень больших чисел или "исчезновения порядка"
- 40. Ненормализованная форма. Основание степени 2 Для приведения к нормализованному виду нужно сдвинуть мантиссу влево на 11
- 41. Ненормализованная форма. Основание степени 16 Для приведения к нормализованному виду нужно сдвинуть мантиссу влево на 2
- 42. Стандарт IEEE 754 1985 г. институт IEEE выпустил стандарт IEEE 754, которому в настоящее время соответствуют
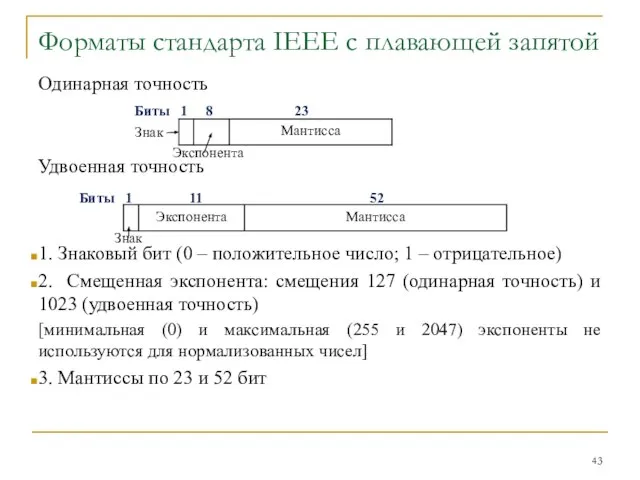
- 43. Форматы стандарта IEEE с плавающей запятой Одинарная точность Удвоенная точность 1. Знаковый бит (0 – положительное
- 44. Форматы стандарта IEEE с плавающей запятой Нормализованная мантисса начинается с двоичной точки за которой следует 1
- 45. Числовые типы стандарта IEEE Если модуль результата меньше самого маленького нормал-ого числа с плавающей точкой =>
- 46. Форматы стандарта IEEE с плавающей запятой Самое маленькое число 1,0×2^(-126) [1 в экспоненте и 0 в
- 48. Скачать презентацию












































 Устройства хранения информации
Устройства хранения информации Чему я научилась на уроках информатики
Чему я научилась на уроках информатики Информатика в играх и задачах. Основы логики. 2 класс ( 3 урок)
Информатика в играх и задачах. Основы логики. 2 класс ( 3 урок) PixelBox™
PixelBox™ Верстальщик HTML
Верстальщик HTML Кодирование графической информации
Кодирование графической информации Информатика. Основные понятия и определения
Информатика. Основные понятия и определения Презентация "MSC.Mvision Workshop 3" - скачать презентации по Информатике
Презентация "MSC.Mvision Workshop 3" - скачать презентации по Информатике Защищенность данных в сети. Занятие 1
Защищенность данных в сети. Занятие 1 Лекция 1. Стандартизация программных средств: общие положения
Лекция 1. Стандартизация программных средств: общие положения Информационных технологиях на предприятии Студентка гр. 06011106 Кузубова наталья Что я знаю о
Информационных технологиях на предприятии Студентка гр. 06011106 Кузубова наталья Что я знаю о  Мастер-класс продвижение в социальных сетях для экспертов
Мастер-класс продвижение в социальных сетях для экспертов Эволюция игровых консолей
Эволюция игровых консолей Разработка мобильного приложения тема
Разработка мобильного приложения тема Основные типы данных языка Паскаль
Основные типы данных языка Паскаль Создание документов на базе комплекса программных средств электронного офиса Microsoft Office
Создание документов на базе комплекса программных средств электронного офиса Microsoft Office Информационный процесс накопления данных
Информационный процесс накопления данных ER моделирование
ER моделирование Управление процессами
Управление процессами Интерфейс. Программный комплекс
Интерфейс. Программный комплекс Обработка изображений
Обработка изображений Этапы разработки базы данных дата проведения: 04.02.09 Провела: Учитель информатики и ВТ Хрусцелевская Н.В. Прослушал: 11 класс
Этапы разработки базы данных дата проведения: 04.02.09 Провела: Учитель информатики и ВТ Хрусцелевская Н.В. Прослушал: 11 класс Как работает Brand Lift? Надежный дизайн исследований
Как работает Brand Lift? Надежный дизайн исследований Решение задач с использованием оператора циклов
Решение задач с использованием оператора циклов Информационная система
Информационная система Компьютерная графика
Компьютерная графика “AVTO” мобильді қосымшасы
“AVTO” мобильді қосымшасы Internet технологии. Лекция 7.1
Internet технологии. Лекция 7.1