Содержание
- 2. Definition 1.1: The fundamental problem of communication is that of reproducing at one point either exactly
- 3. “THEN, OUR PROBLEM IS THE NOISE!” Information Theory How can we achieve perfect communication over an
- 4. The theory provides answers to two fundamental questions (among others): What is the irreducible complexity below
- 5. The information theory (IT) frame work: Communication System Line Coding Channel Coding (Shannon's 2nd theorem) Cryptology
- 6. The information theory (IT) frame work: Communication System Line Coding Channel Coding (Shannon's 2nd theorem) Cryptology
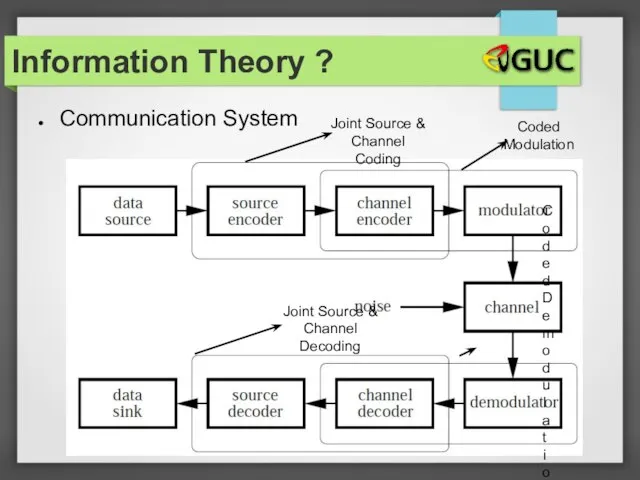
- 7. Communication System Information Theory ?
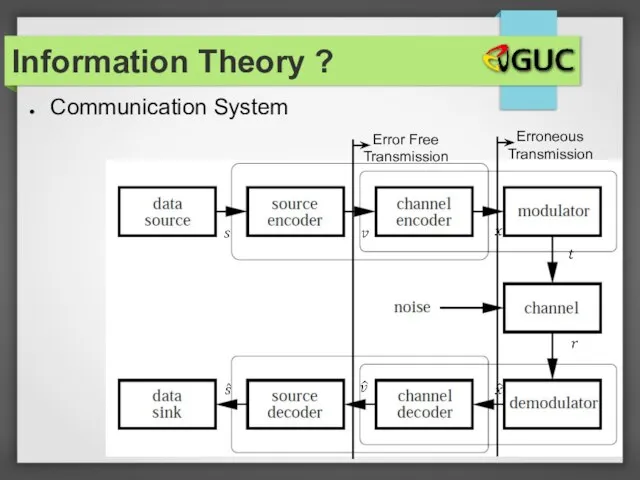
- 8. Communication System Error Free Transmission Erroneous Transmission Information Theory ?
- 9. The information theory (IT) frame work: Communication System Line Coding Channel Coding (Shannon's 2nd theorem) Cryptology
- 10. Also known as digital baseband modulation (1,0,1,1,0, … ) encoding digital information to make it resistant
- 11. The information theory (IT) frame work: Communication System Line Coding Channel Coding (Shannon's 2nd theorem) Cryptology
- 12. The Three Channel Properties Channels can only transport physical signals, e.g., electrical signals. Therefore, digital signals
- 13. A.K.A: Forward error correction (FEC) For controlling errors in data transmission over unreliable (generally → noisy)
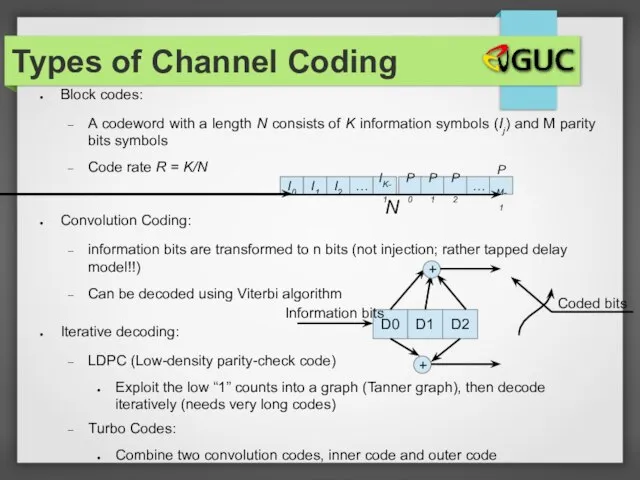
- 14. Types of Channel Coding Block codes: A codeword with a length N consists of K information
- 15. The information theory (IT) frame work: Communication System Line Coding Channel Coding (Shannon's 2nd theorem) Cryptology
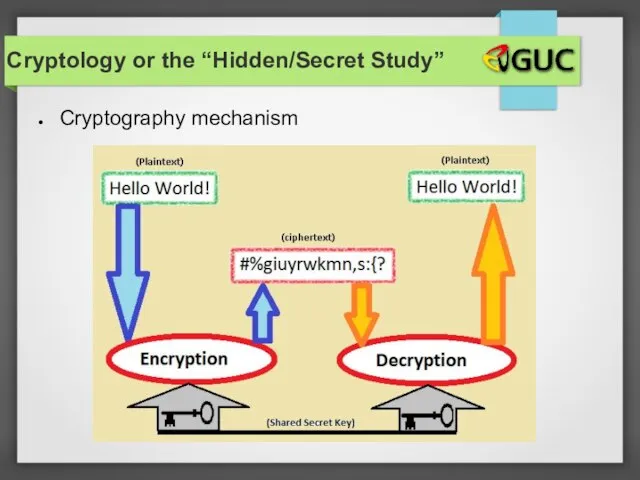
- 16. Cryptology or the “Hidden/Secret Study” Cryptography mechanism
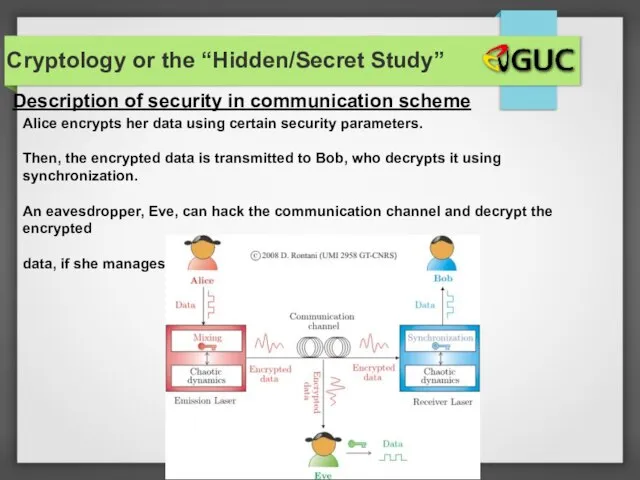
- 17. Cryptology or the “Hidden/Secret Study” Alice encrypts her data using certain security parameters. Then, the encrypted
- 18. Cryptology World War II The German Lorenz cipher SZ42 (SZ for Schlüsselzusatz), one of the first
- 19. The information theory (IT) frame work: Communication System Line Coding Channel Coding (Shannon's 2nd theorem) Cryptology
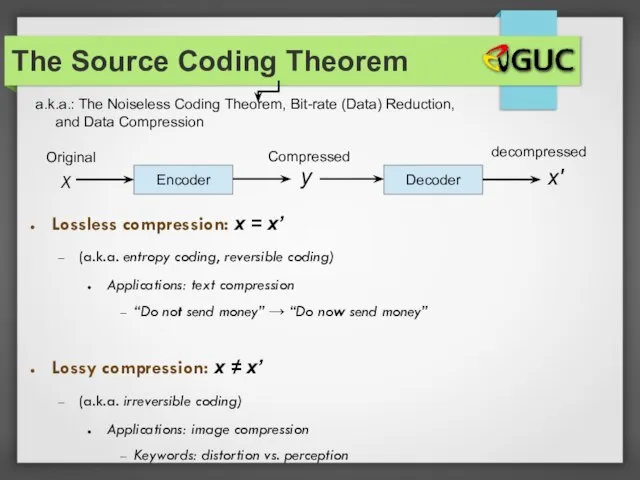
- 20. a.k.a.: The Noiseless Coding Theorem, Bit-rate (Data) Reduction, and Data Compression The Source Coding Theorem Encoder
- 21. The Source Coding Theorem High comp. (98% less info) 1.14 KB) Original (108.5 KB) Medium comp.
- 22. Compression Measurement Criteria Compression ratio:|x|/|y| |x| represents the number of bits in y E.g.: |x| =
- 23. Now we will learn 3 concepts: Self-information Entropy Kraft's inequality The Source Coding Theorem
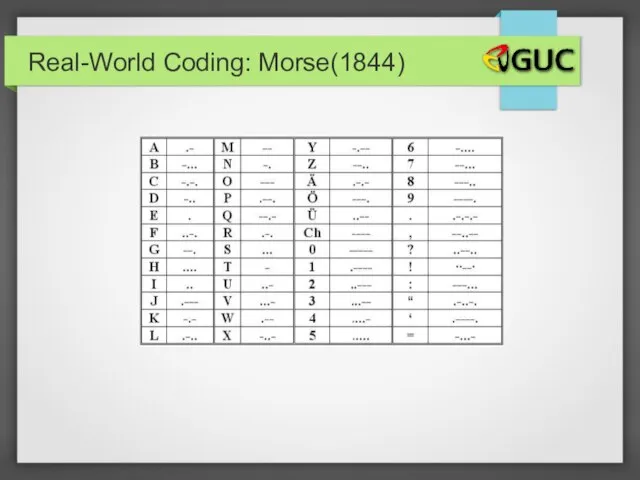
- 24. Real-World Coding: Morse(1844)
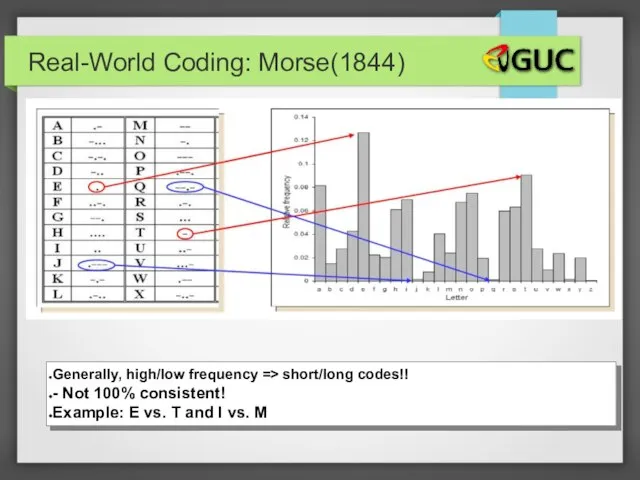
- 25. Real-World Coding: Morse(1844) Generally, high/low frequency => short/long codes!! - Not 100% consistent! Example: E vs.
- 26. Assume: A source with finite number of symbols S ={s1, s2, ..., sN} Symbol sn has
- 27. Properties of self-information: barking of a dog during breaking a house carry or does not carry
- 28. Self-Information Examples Example 1: the out come of flipping a coin if: The coin is fair,
- 29. Entropy as Information Content Entropy is a probabilistic model such that: Independent fair coin flips have
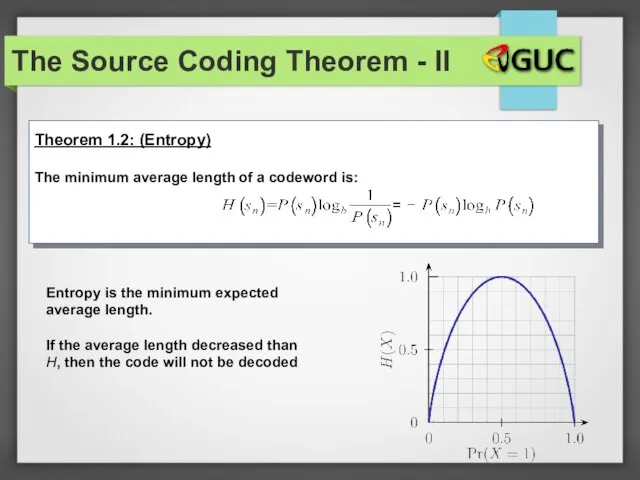
- 30. The Source Coding Theorem - II Theorem 1.2: (Entropy) The minimum average length of a codeword
- 31. The Source Coding Theorem - III Code Word and Code Length: Definition 1.2: A (binary) source
- 32. The Source Coding Theorem – IV Can you say why?
- 33. The Source Coding Theorem - V Conversely, given a set of codeword lengths satisfying the above
- 34. The Source Coding Theorem – IV Do It Your Self!!
- 35. Notation for Sequences & Codes Assume a sequence of symbols X = {X1;X2; … ;Xn} from
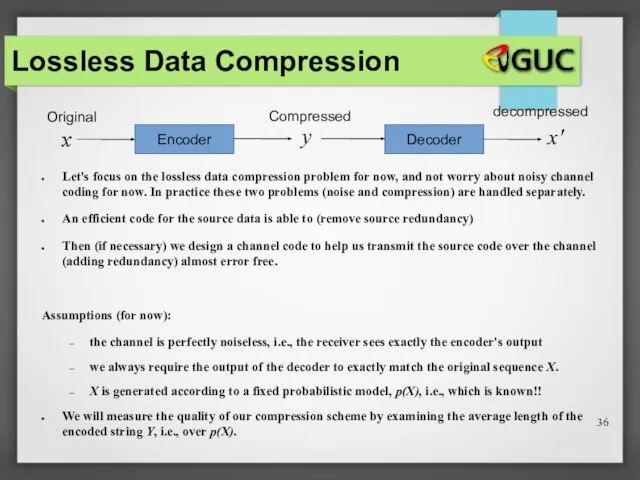
- 36. Lossless Data Compression Let's focus on the lossless data compression problem for now, and not worry
- 38. Скачать презентацию

























 Объектно-ориентированное программирование. Наследование
Объектно-ориентированное программирование. Наследование Szkolenie techniczne 2. (Zajęcia 2)
Szkolenie techniczne 2. (Zajęcia 2) Презентация "Введение в мультимедийные базы данных" - скачать презентации по Информатике
Презентация "Введение в мультимедийные базы данных" - скачать презентации по Информатике Клавиатура, ее назначением и принцип действия
Клавиатура, ее назначением и принцип действия Технологии видеомонтажа
Технологии видеомонтажа Web-страницы и Web-сайты
Web-страницы и Web-сайты Средства автоматизации проектирования
Средства автоматизации проектирования Вирусные программы под мобильные платформы
Вирусные программы под мобильные платформы Константы
Константы SEO продвижение сайта своими руками
SEO продвижение сайта своими руками Разработка информационной системы для автоматизации работы склада
Разработка информационной системы для автоматизации работы склада Хайрулина А.В., учитель информатики, МОУ СОШ №10, г.Кандалакша, Мурманской области
Хайрулина А.В., учитель информатики, МОУ СОШ №10, г.Кандалакша, Мурманской области  Управління даними (файли і файлові системи)
Управління даними (файли і файлові системи) История ПК. Архитектура ПК
История ПК. Архитектура ПК Мережа Кохонена
Мережа Кохонена Информационные модели. Модель и моделирование
Информационные модели. Модель и моделирование Использование Amazon Web Services
Использование Amazon Web Services Способы передачи электронных документов
Способы передачи электронных документов Майнкрафт— компьютерная инди-игра
Майнкрафт— компьютерная инди-игра Методы защиты информации. Информационная безопасность. Лекция 4
Методы защиты информации. Информационная безопасность. Лекция 4 Архитектура операционных систем. Лекция1
Архитектура операционных систем. Лекция1 Характеристика табличных и графических редакторов
Характеристика табличных и графических редакторов Формирование изображения на экране монитора
Формирование изображения на экране монитора Отношения между объектами
Отношения между объектами Сценарии использования Системы
Сценарии использования Системы Получение доступа к ресурсам портала ZAсобой
Получение доступа к ресурсам портала ZAсобой ER моделирование
ER моделирование Регламент мастер-класса Мужчина нарасхват
Регламент мастер-класса Мужчина нарасхват