Содержание
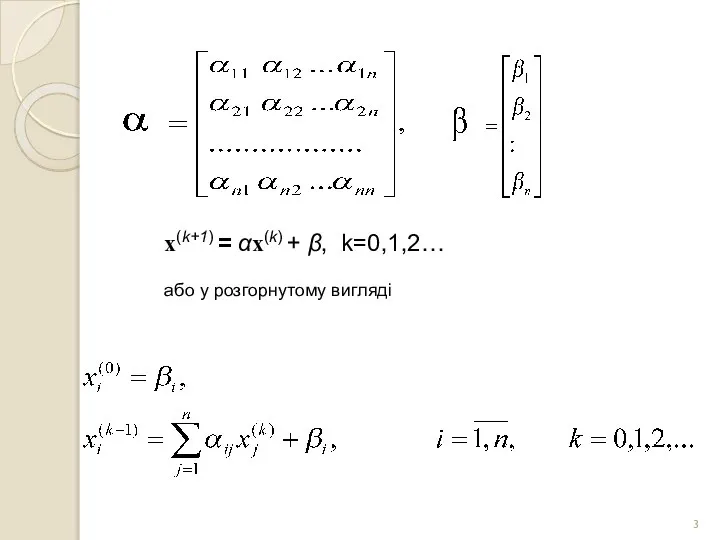
- 2. МЕТОД ПРОСТОЇ ІТЕРАЦІЇ Припустимо, що і перетворимо систему до вигляду
- 3. x(k+1) = αx(k) + β, k=0,1,2… або у розгорнутому вигляді
- 7. ЗБІЖНІСТЬ МЕТОДУ ПРОСТОЇ ІТЕРАЦІЇ Для збіжності процесу обчислень необхідно, щоб виконувалась умова ||α|| Відповідно для різних
- 8. Теорема Якщо матриця α системи рівнянь x(k+1) = αx(k) + β задовольняє одну із умов то
- 9. ПОХИБКИ МЕТОДУ ПРОСТОЇ ІТЕРАЦІЇ Глобальна похибка розв’язку на двох сусідніх ітераціях ||x(k+1) – x*|| = ||α||
- 10. МЕТОД ЯКОБІ Запишемо метод Якобі в матричній формі. Для цього запишемо матрицю A як: A =
- 11. МЕТОД ЯКОБІ Запишемо СЛАР як: (L + D + U)x = b або Dx = b
- 12. МЕТОД ЯКОБІ При цьому Для збіжності методу Якобі достатньо, щоб матриця α мала домінуючу головну діагональ:
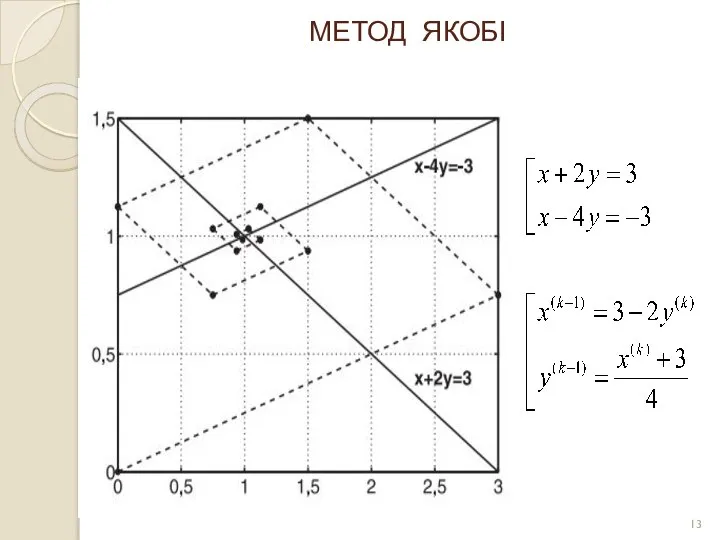
- 13. МЕТОД ЯКОБІ
- 14. МЕТОД ГАУССА-ЗЕЙДЕЛЯ Маємо (L + D)x = b - Ux У матричній формі метод Гаусса-Зейделя записується
- 17. ПОХИБКИ МЕТОДУ ГАУССА-ЗЕЙДЕЛЯ Локальна похибка за наближеннями, що отримані на двох сусідніх ітераціях Метод Гаусса-Зейделя слід
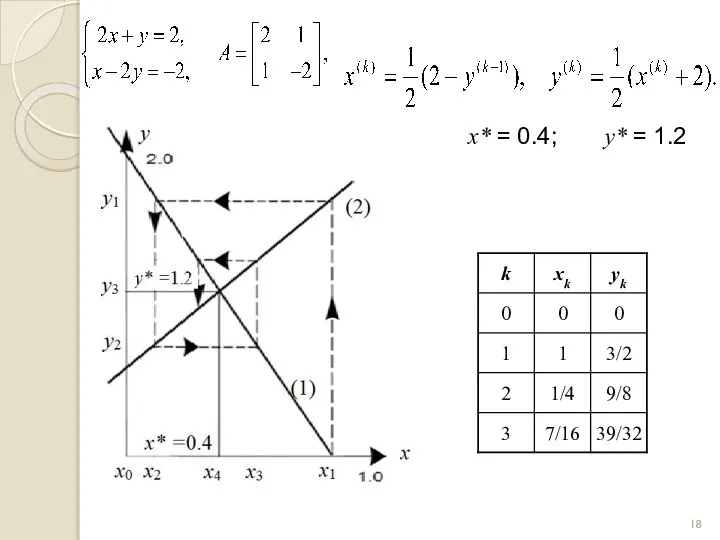
- 18. x* = 0.4; y* = 1.2
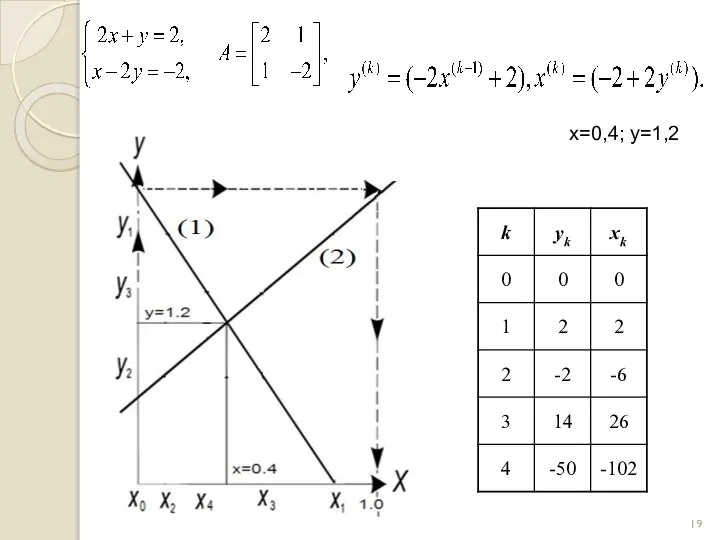
- 19. x=0,4; y=1,2
- 20. КАНОНІЧНА ФОРМА ІТЕРАЦІЙНИХ МЕТОДІВ Канонічною формою однокрокових ітераційних методів розв’язування СЛАР називається їх запис у вигляді:
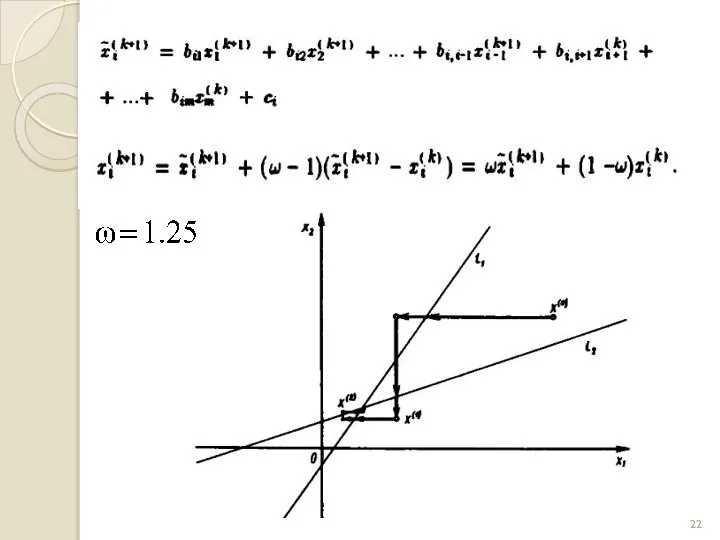
- 21. МЕТОД РЕЛАКСАЦІЇ Умови збіжності можна покращити, якщо ввести коефіцієнт демпфірування для врахування нев’язки Тоді метод простої
- 25. Метод релаксації
- 26. РОЗВ’ЯЗАННЯ СИСТЕМ НЕЛІНІЙНИХ РІВНЯНЬ У загальному випадку системa нелінійних рівнянь записується у вигляді де − функції
- 27. Для методу простої ітерації можна записати: де На першій ітерації на основі початкового наближення наступне знаходять
- 28. де – матриця Якобі, Одним із серйозних недоліків методу простих ітерацій є складність вибору функцій які
- 29. Узагальнений метод Ньютона:
- 34. Скачать презентацию























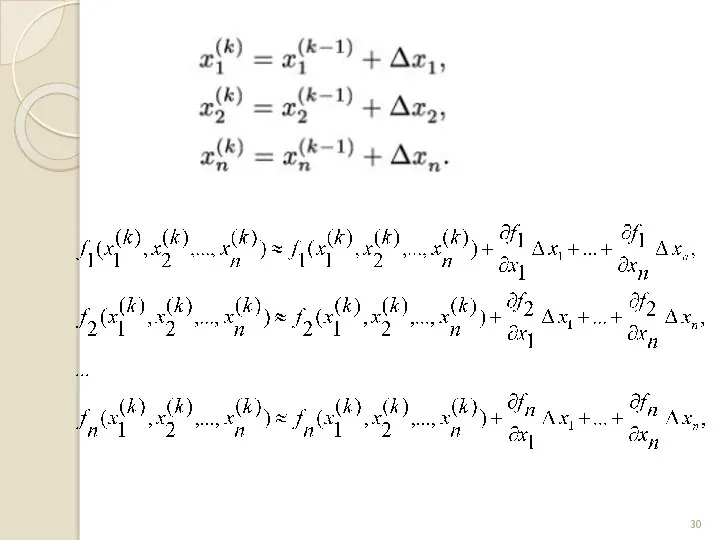

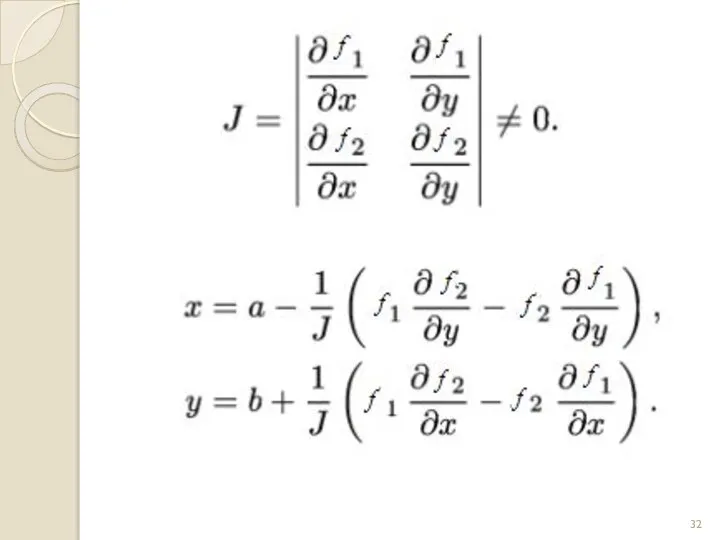
 Геометрические ребусы
Геометрические ребусы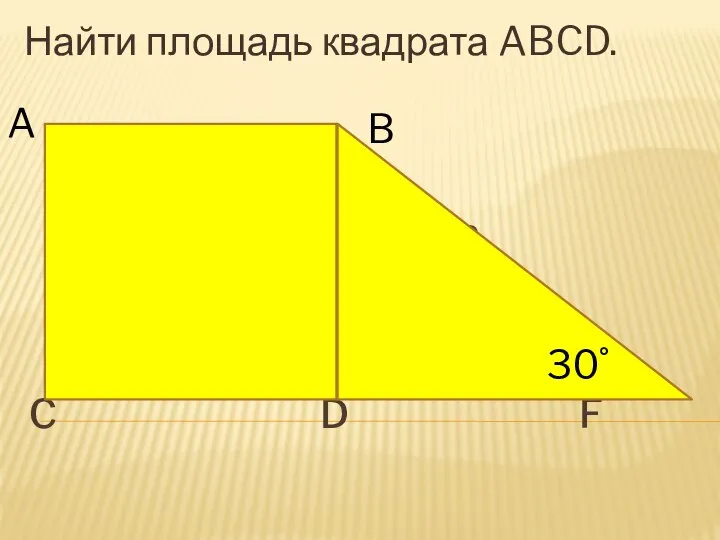 Решение задач. Площадь квадрата
Решение задач. Площадь квадрата Рентгеновское излучение. Основы компьютерной томографии. Введение в интроскопию
Рентгеновское излучение. Основы компьютерной томографии. Введение в интроскопию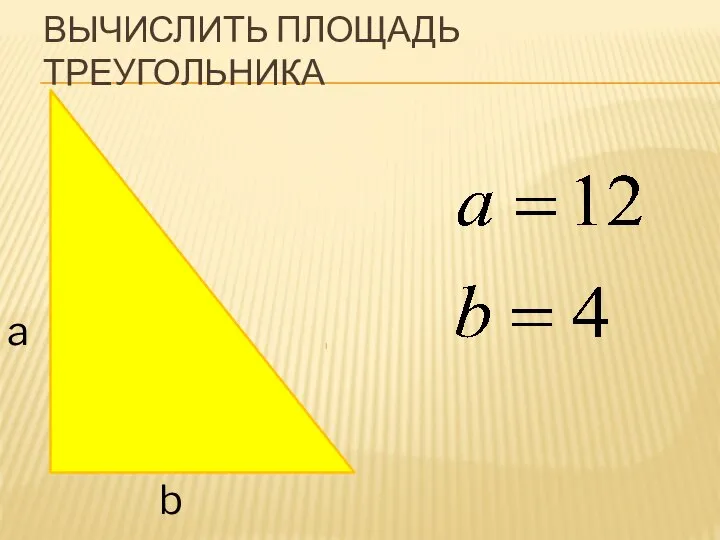 Вычисление площади треугольника
Вычисление площади треугольника Уравнения n-ой степени
Уравнения n-ой степени Задачи в УМК Г.К. Муравин, О.В.Муравина развивающие творческие способности учащихся
Задачи в УМК Г.К. Муравин, О.В.Муравина развивающие творческие способности учащихся Конус и его применение в быту
Конус и его применение в быту Система счисления (задания)
Система счисления (задания)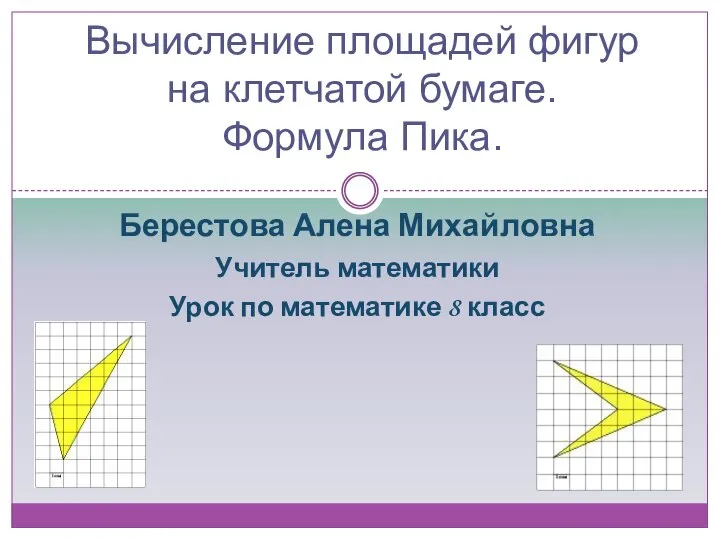 Вычисление площадей фигур на клетчатой бумаге. Формула Пика
Вычисление площадей фигур на клетчатой бумаге. Формула Пика Қарапайым математикалық түсініктер. Уақытты бағдарлау
Қарапайым математикалық түсініктер. Уақытты бағдарлау Планиметрия. Четырёхугольники
Планиметрия. Четырёхугольники Действия с натуральными числами. Прикидка и оценка
Действия с натуральными числами. Прикидка и оценка Презентация на тему Сравнение натуральных чисел
Презентация на тему Сравнение натуральных чисел Быстрый счет. Табличное сложение чисел от 11 до 20
Быстрый счет. Табличное сложение чисел от 11 до 20 Второй признак равенства треугольников. Математический диктант
Второй признак равенства треугольников. Математический диктант Модуль действительного числа. (8 класс)
Модуль действительного числа. (8 класс) Математическая викторина "Что? Где? Когда?"
Математическая викторина "Что? Где? Когда?" Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни Свойства функций, непрерывных на отрезке
Свойства функций, непрерывных на отрезке Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс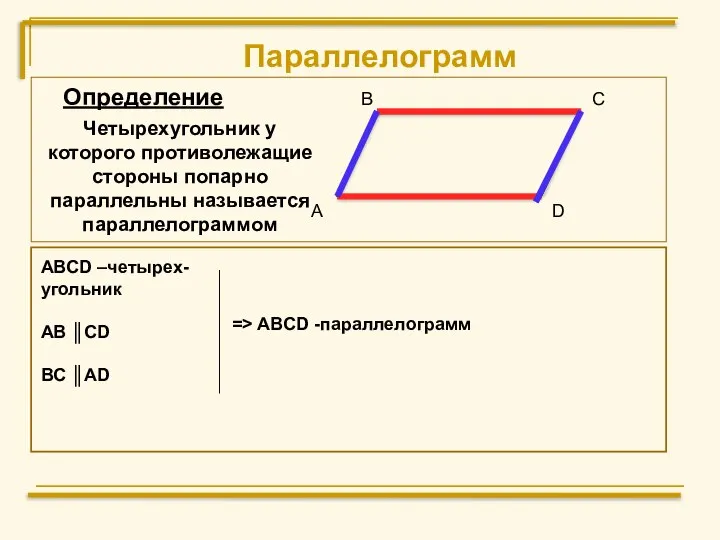 Параллелограмм
Параллелограмм Возведение в куб суммы и разности
Возведение в куб суммы и разности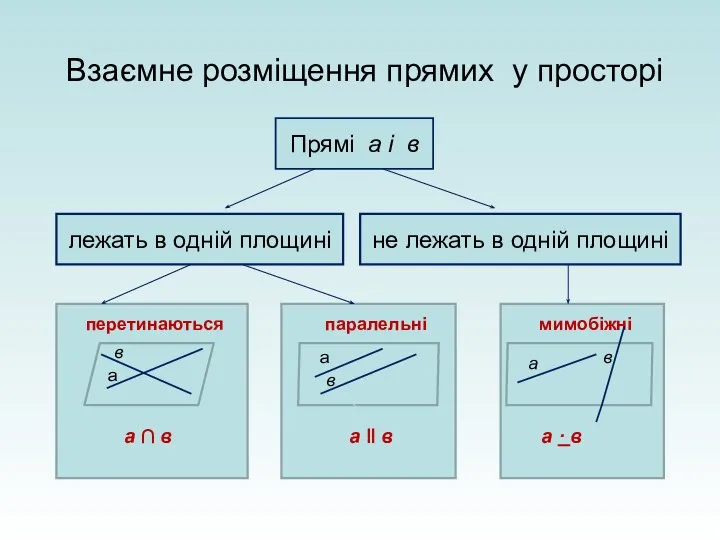 Взаємне розміщення прямих у просторі
Взаємне розміщення прямих у просторі Анализ упражнений на нумерацию в концентре тысяча и концентре многозначные числа в учебниках по математике Л.Г.Петерсон
Анализ упражнений на нумерацию в концентре тысяча и концентре многозначные числа в учебниках по математике Л.Г.Петерсон Елементи теорії формальних мов. (Тема 2)
Елементи теорії формальних мов. (Тема 2) Равные множества. (1 класс)
Равные множества. (1 класс) График функции y = f( x + l)
График функции y = f( x + l) Сравнение дробей. 5 класс
Сравнение дробей. 5 класс