Содержание
- 2. Урок № 1 Логика как наука. Формы человеческого мышления Урок № 2 Логические операции. Построение таблиц
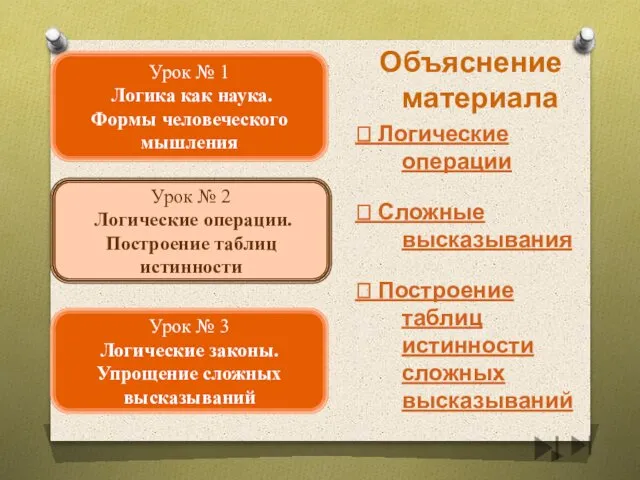
- 3. Объяснение материала ? Об истории логики ? Область применения алгебры логики ? Основные понятия логики Урок
- 4. Объяснение материала ? Логические операции ? Сложные высказывания ? Построение таблиц истинности сложных высказываний Урок №
- 5. Объяснение материала ? Законы логики ? Упрощение сложных высказываний Урок № 1 Логика как наука. Формы
- 6. Об истории логики Термин логика происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон». Логика
- 7. Основоположник формальной логики Аристотель (384 - 322 гг. до н.э.)
- 8. Рене Декарт (1596 - 1650) Рекомендовал в логике использовать общепринятые математические методы.
- 9. Предложил использовать в логике математическую символику и впервые высказал мысль о возможности применения в ней двоичной
- 10. Основоположник алгебры логики (булевой алгебры) Джордж Буль (1815 - 1864)
- 11. Большой вклад в становление и развитие математической логики внесли многие выдающиеся математики и логики XVI -
- 12. Область применения алгебры логики Алгебра логики сегодня - раздел математической логики, изучающий строение (форму, структуру) сложных
- 13. Мыслить логично - значит мыслить точно и последовательно, не допуская противоречий в своих рассуждениях, уметь вскрывать
- 14. ☞ в вычислительной технике; ☞ в логических построениях в математике; ☞ в повседневных рассуждениях. Практическое применение
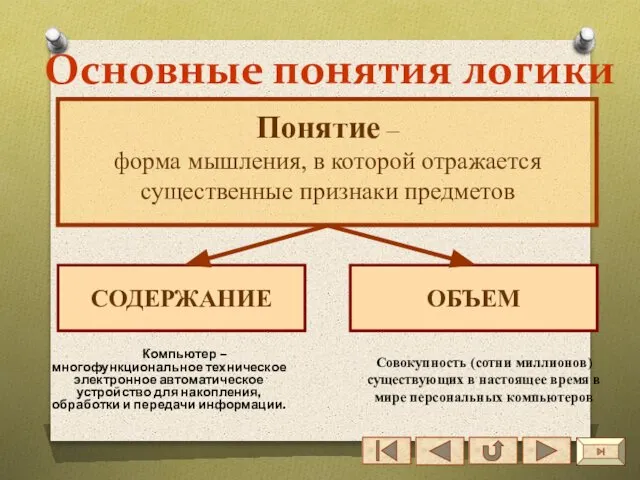
- 15. Основные понятия логики Компьютер – многофункциональное техническое электронное автоматическое устройство для накопления, обработки и передачи информации.
- 16. Виды понятий Несравнимые Сравнимые Совместимые Несовместимые далекие друг от друга по своему содержанию понятия, не имеющие
- 17. Физкультминутка Упражнение первое: сжимать и разжимать кулаки. Повторить 4- 5 раз. Упражнение второе: вращать кистями рук
- 18. Основные понятия логики Суждение (высказывание, утверждение) - повествовательное предложение, относительно которого можно сказать, истинно оно или
- 19. Не являются суждениями: Предложения, о которых нельзя сказать, истинны они или ложны. Вопросительные и восклицательные предложения.
- 20. Виды суждений Частные Общие Простые Сложные Равносильные (эквивалентные) выражают конкретные факты. характеризуют свойства групп объектов (явлений).
- 21. Основные понятия логики Умозаключение - форма мышления, посредством которой из одного или нескольких истинных суждений (посылок)
- 22. ? Вопросы и задания 1 Какие из перечисленных ниже предложений являются суждениями? Некоторые люди имеют голубые
- 23. ? Вопросы и задания 2 Укажите для нижеприведенных высказываний, сложные они или простые: Если две прямые
- 24. ? Вопросы и задания 3 "сижу и смотрю"; "сумма внутренних углов треугольника равна двум прямым углам";
- 25. ? Вопросы и задания 4 (X + Y) (X - Y) = X2 - Y2; "Любой
- 26. Физкульминутка Упражнение первое: резко зажмурить глаза на 2-3 секунды: и широко открыть на 2-3 секунды, повторить
- 27. Логические операции способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью
- 28. Логическое отрицание -ИНВЕРСИЯ Образуется из высказывания с помощью добавления частицы «НЕ» к сказуемому или использования оборота
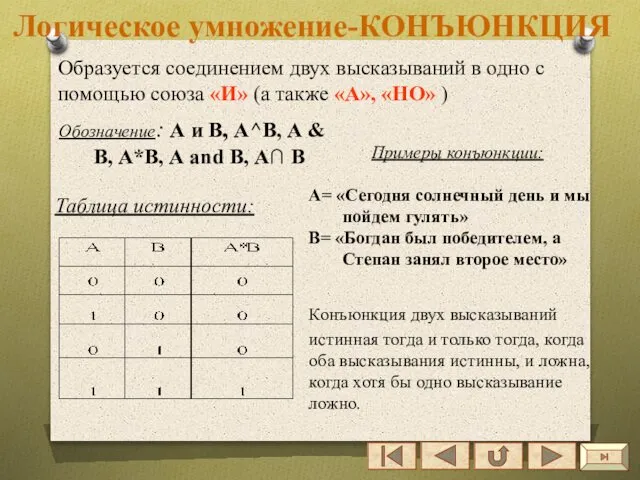
- 29. Логическое умножение-КОНЪЮНКЦИЯ Образуется соединением двух высказываний в одно с помощью союза «И» (а также «А», «НО»
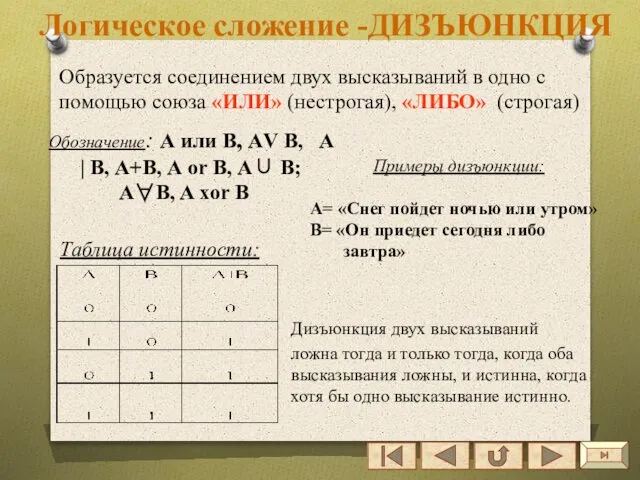
- 30. Логическое сложение -ДИЗЪЮНКЦИЯ Образуется соединением двух высказываний в одно с помощью союза «ИЛИ» (нестрогая), «ЛИБО» (строгая)
- 31. Логическое следование -ИМПЛИКАЦИЯ Образуется соединением двух высказываний в одно с помощью оборота речи «ЕСЛИ …, ТО
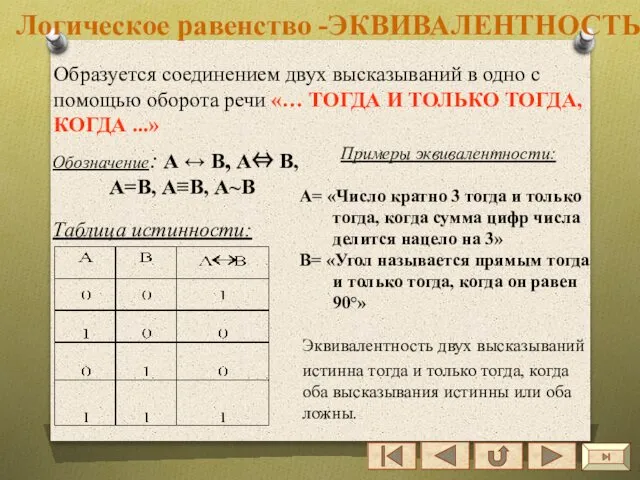
- 32. Логическое равенство -ЭКВИВАЛЕНТНОСТЬ Образуется соединением двух высказываний в одно с помощью оборота речи «… ТОГДА И
- 33. Свойства логических операций Инверсия истинна высказывание ложно Дизъюнкция ложна Конъюнкция истинна оба высказывания ложны истинны Дизъюнкция
- 34. Перевод логических операций на естественный язык Инверсия Конъюнкция Дизъюнкция Импликация Эквивалентность не А; неверно, что А
- 35. Приоритет логических операций инверсия конъюнкция дизъюнкция импликация эквивалентность Операции одного приоритета выполняются слева направо. Для изменения
- 36. Пример 1 Дана формула: А V В ⇒ С & D ⇔ Ā Порядок вычисления: Ā
- 37. Пример 2 Дана формула: А V (В ⇒ С) & D ⇔ Ā Порядок вычисления: Ā
- 38. Сложные высказывания Если несколько простых высказываний объединены в одно с помощью логических операций, то такое высказывание
- 39. Тождественно истинные, тождественно ложные и эквивалентные высказывания Если высказывание истинно при всех значениях входящих в него
- 40. Задача № 1 Укажите значения истинности простых высказываний, при которых суждение «Если у меня будет свободное
- 41. Задача № 1 Решение В = «У меня будет свободное время» Е = «Я сдам экзамены»
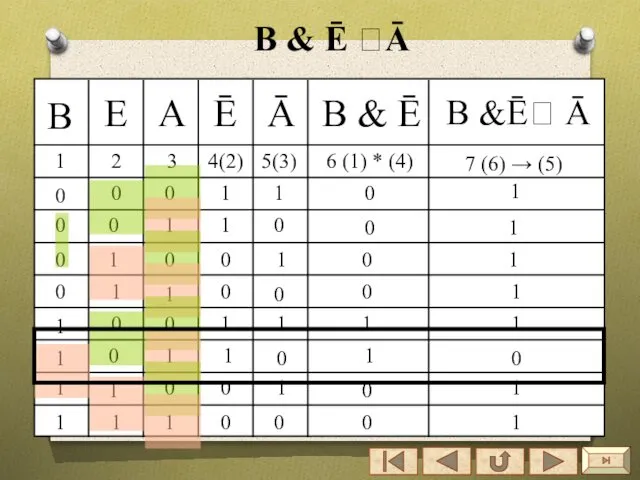
- 42. Построение таблиц истинности сложных высказываний Построить таблицу истинности для высказывания B & Ē ? Ā Алгоритм
- 43. 1 3 4(2) 5(3) 6 (1) * (4) 7 (6) → (5) 0 0 0 1
- 44. Законы логики
- 45. Закон тождества: в процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе. А
- 46. Закон непротиворечия: невозможно, чтобы одно и тоже в одно и тоже время было и не было
- 47. Закон исключения третьего: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано. А
- 48. Закон достаточного основания: всякая истинная мысль должна быть достаточно обоснована.
- 49. Закон двойного отрицания: если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание. А =
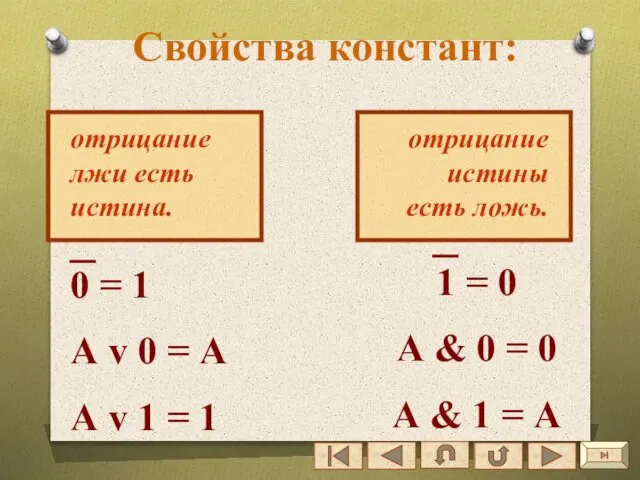
- 50. Свойства констант: отрицание лжи есть истина. 0 = 1 А v 0 = А А v
- 51. Закон идемпотентности: А v А = А А & А = A
- 52. Законы коммутативности (сочетательные законы): операнды А и В в операциях дизъюнкции и конъюнкции можно менять местами.
- 53. Законы ассоциативности (распределительные законы): если в выражении используется только операция дизъюнкции или только операция конъюнкции, то
- 54. Законы дистрибутивности: А v (В & C) = (А v В) & (А v C) А
- 55. Законы поглощения: А & (В v B) = А или А & (А v В) =
- 56. Законы де Моргана: отрицание дизъюнкции есть конъюнкция отрицаний. Отрицание конъюнкции есть дизъюнкция отрицаний. А v В
- 57. Правило замены операции импликации: А ⇒ В = А v В
- 58. Правило замены операции эквивалентности: А ⇔ В = В ⇔ А А ⇔ В = (А
- 59. Доказательство логических законов построить таблицу истинности для правой и левой частей равенства; выполнить эквивалентные преобразования над
- 60. Упрощение сложных высказываний
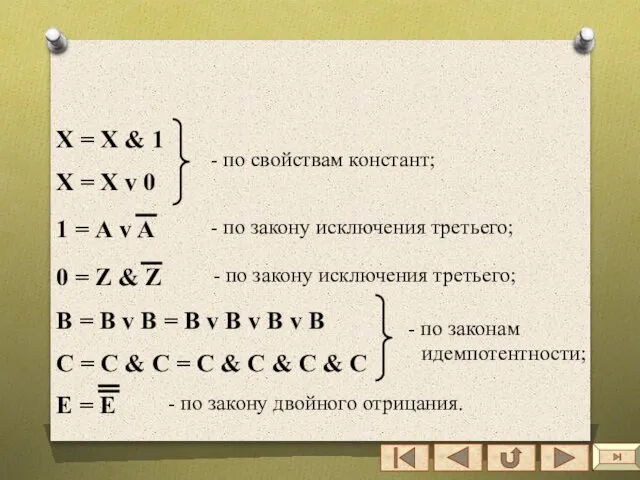
- 61. X = X & 1 X = X v 0 1 = А v A 0
- 62. Задача № 2 «Уроки логики» На вопрос, кто из трех школьников изучал логику, был получен правильный
- 63. Задача № 2 «Уроки логики» Решение: Р1 = «Первый школьник изучал логику» Р2 = «Второй школьник
- 64. Задача № 2 «Уроки логики» (Р1 → Р2) & (Р3 → Р2) = = (P1 v
- 65. Пример 3 Требуется упростить: А & B v A & B По закону дистрибутивности вынесем А
- 66. Пример 4 Требуется упростить: (А v B) & (A v B) Способ 1. Применим закон дистрибутивности:
- 67. Пример 5 Требуется упростить: X v X & Y Представим Х как Х & 1, а
- 68. Пример 6 Требуется упростить: А & C v B & C v А & B Добавим
- 69. Пример 7 Требуется упростить: X v Y Применим закон де Моргана: X v Y = X
- 70. Пример 8 Требуется упростить: X & Y v X & Y v X & Z В
- 72. Скачать презентацию





























































 Математика. Решение задач
Математика. Решение задач Действия с натуральными числами. Урок-сказка
Действия с натуральными числами. Урок-сказка Производная сложной функции
Производная сложной функции Начертательная геометрия. Метод проекций
Начертательная геометрия. Метод проекций Математические ребусы. 6 класс
Математические ребусы. 6 класс Игра для 5 класса
Игра для 5 класса Действия с геометрическими фигурами, координатами и векторами
Действия с геометрическими фигурами, координатами и векторами Аксонометрическая проекция окружности
Аксонометрическая проекция окружности Структурные схемы и их преобразование. Типовые динамические звенья САУ и их классификация
Структурные схемы и их преобразование. Типовые динамические звенья САУ и их классификация Теория множеств. Понятие множества
Теория множеств. Понятие множества Заинька. Математическая раскраска. Реши примеры и покажи ответы
Заинька. Математическая раскраска. Реши примеры и покажи ответы Презентация по математике "Способы записи чисел" - скачать
Презентация по математике "Способы записи чисел" - скачать  Екі айнымалысы бар сызықтық теңдеудің графигі
Екі айнымалысы бар сызықтық теңдеудің графигі Векторы на плоскости
Векторы на плоскости Презентация по математике "Проценты. Начальные понятия" - скачать
Презентация по математике "Проценты. Начальные понятия" - скачать  Золотое сечение
Золотое сечение Свойства функций у = tgx и y = ctgx и их графики
Свойства функций у = tgx и y = ctgx и их графики 20160720_simmetriya
20160720_simmetriya Математика в поэзии
Математика в поэзии Деление с остатком
Деление с остатком Вписанная и описанная окружности
Вписанная и описанная окружности Обернена тригонометрична функція y=arcsinx
Обернена тригонометрична функція y=arcsinx Решение задач по теме «Площадь круга»
Решение задач по теме «Площадь круга» Графики квадратичных функций
Графики квадратичных функций Успешные люди – люди, которые в полной мере используют свой интеллект
Успешные люди – люди, которые в полной мере используют свой интеллект Применение первого признака равенства треугольников к решению задач
Применение первого признака равенства треугольников к решению задач «Своя игра». Внеклассное мероприятие по математике
«Своя игра». Внеклассное мероприятие по математике Автор: Галдин В. А. Учитель математики и физики МБОУ ЛСОШ №3 п. Локоть Брасовского р-на Электронная поста: galdin.vas@yandex.ru
Автор: Галдин В. А. Учитель математики и физики МБОУ ЛСОШ №3 п. Локоть Брасовского р-на Электронная поста: galdin.vas@yandex.ru