Содержание
- 2. Geometria obliczeniowa Dział informatyki zajmujący się algorytmami geometrycznymi nazywamy geometrią obliczeniową. Najczęściej rozpatrywane są problemy: Na
- 3. Geometria obliczeniowa Rozważania ograniczamy do geometrii na płaszczyźnie. Podstawowe obiekty geometryczne: punkt p reprezentujemy parą współrzędnych
- 4. Podstawowe fakty z geometrii obliczeniowej na płaszczyźnie
- 5. Podstawowe fakty z geometrii obliczeniowej na płaszczyźnie Punkt r leży po lewej stronie wektora p→q. Punkty
- 6. Elementarne algorytmy Zadanie Sprawdzić, czy punkty r i s leżą po tej samej stronie prostej p−q.
- 7. Elementarne algorytmy Zadanie Kiedy dwa odcinki p−q i r−s przecinają się? Odpowiedź Gdy p i q
- 8. Problem przynależności do wielokąta wypukłego
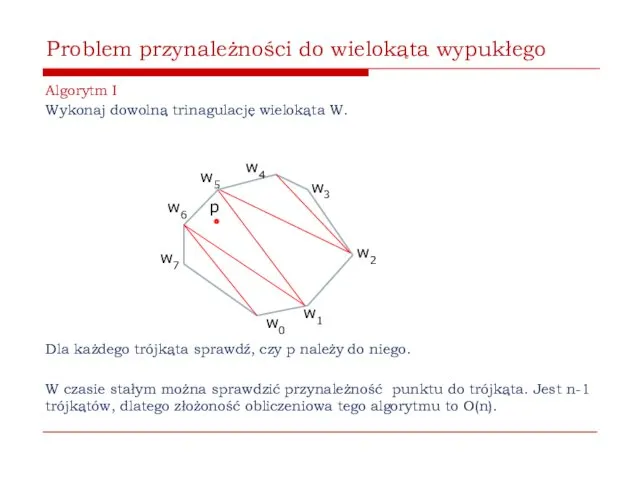
- 9. Problem przynależności do wielokąta wypukłego Algorytm I Wykonaj dowolną trinagulację wielokąta W. Dla każdego trójkąta sprawdź,
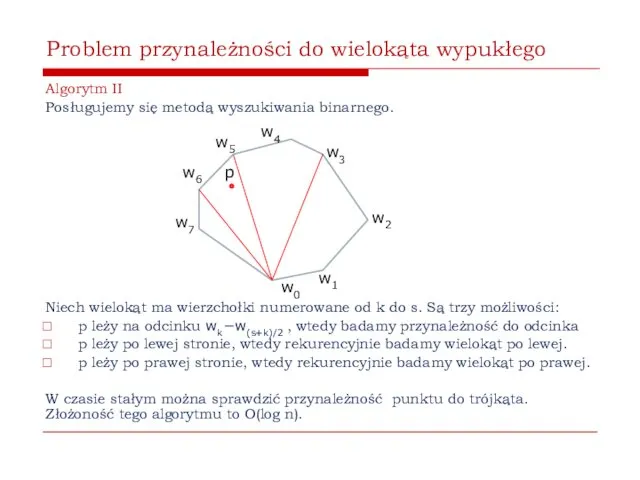
- 10. Problem przynależności do wielokąta wypukłego Algorytm II Posługujemy się metodą wyszukiwania binarnego. Niech wielokąt ma wierzchołki
- 11. Problem przynależności punktu do dowolnego wielokąta Dane: n – liczba naturalna n punktów w0, …, wn-1
- 12. W czasie liniowym umiemy sprawdzić, czy p należy do któregoś z boków wielokąta. Jeśli jest inaczej,
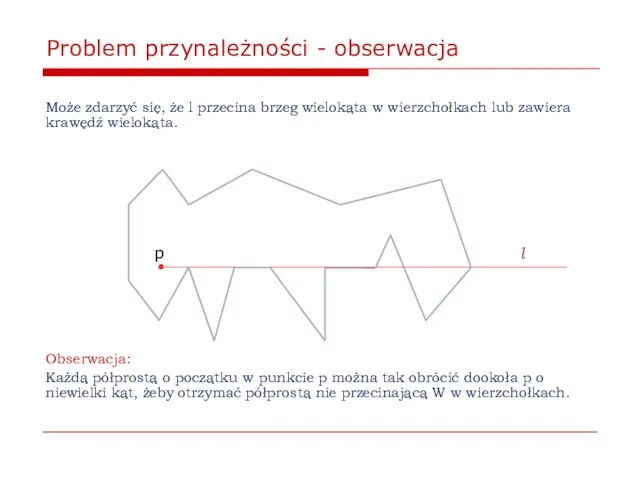
- 13. Problem przynależności - obserwacja Może zdarzyć się, że l przecina brzeg wielokąta w wierzchołkach lub zawiera
- 14. Problem przynależności - przypadki Rozważamy dwa przypadki (i wszystkie analogiczne do nich): Złożoność O(n) – koszt
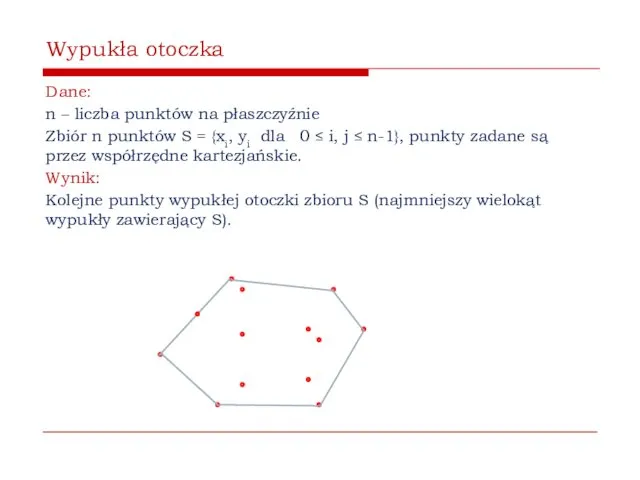
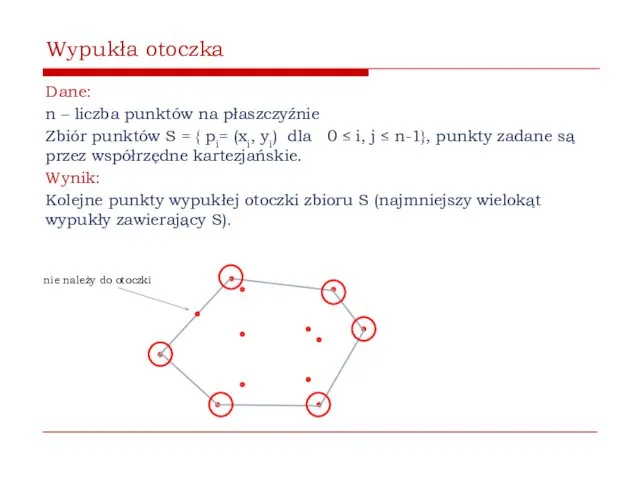
- 15. Wypukła otoczka Dane: n – liczba punktów na płaszczyźnie Zbiór n punktów S = {(xi, yi)
- 16. Wypukła otoczka Dane: n – liczba punktów na płaszczyźnie Zbiór n punktów S = {xi, yi
- 17. Wypukła otoczka Dane: n – liczba punktów na płaszczyźnie Zbiór punktów S = { pi= (xi,
- 18. Wypukła otoczka – algorytm naiwny Krok 1. Znaleźć wszystkie wierzchołki wypukłej otoczki zbioru S. Krok 2.
- 19. Wypukła otoczka – sortowanie biegunowe Układ współrzędnych polarnych – układ współrzędnych na płaszczyźnie wyznaczony przez pewien
- 20. Wypukła otoczka – sortowanie biegunowe x y 0 x2 x1 y2 y1
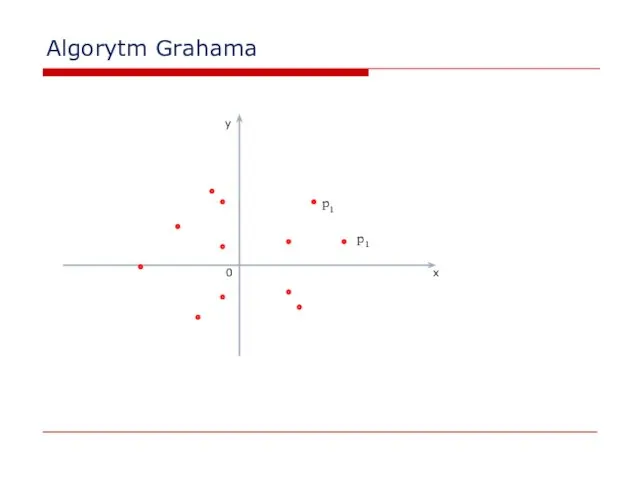
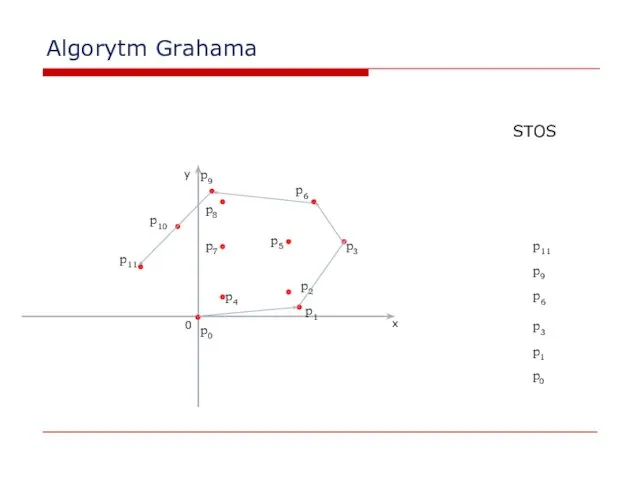
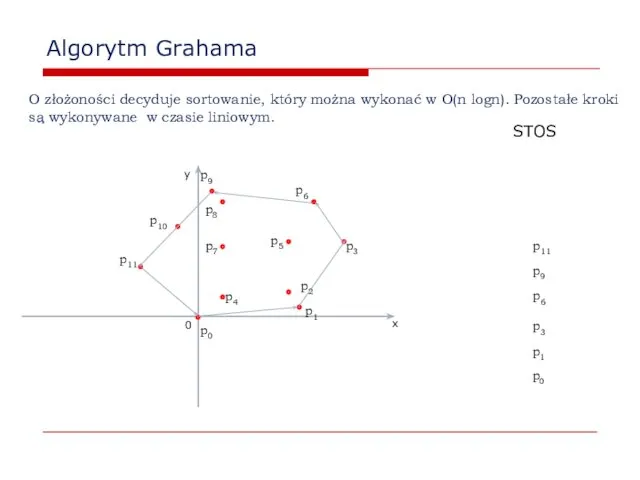
- 21. Algorytm Grahama W algorytmie Grahama używamy stosu, który zawiera kandydatów na wierzchołki otoczki. Każdy punkt z
- 22. Algorytm Grahama 0 x y p1 p1
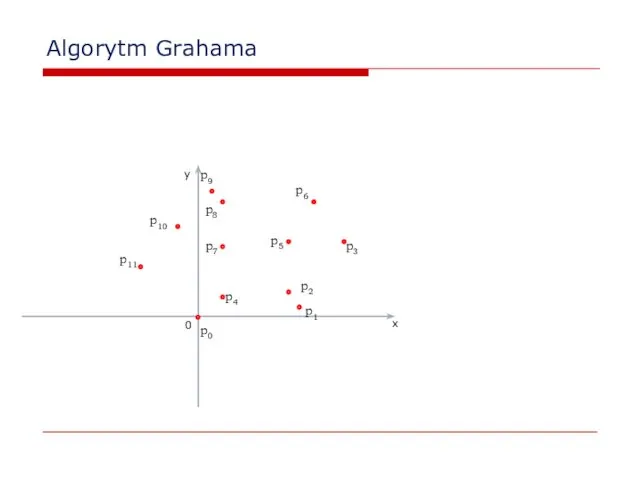
- 23. Algorytm Grahama 0 x y p2 p0 p1 p3 p4 p5 p6 p7 p8 p9 p10
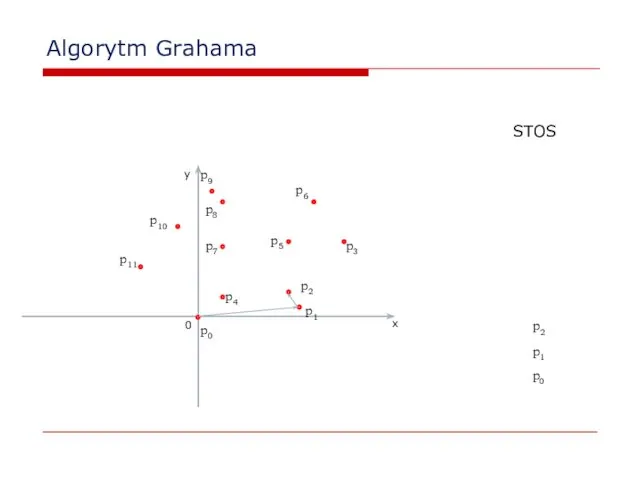
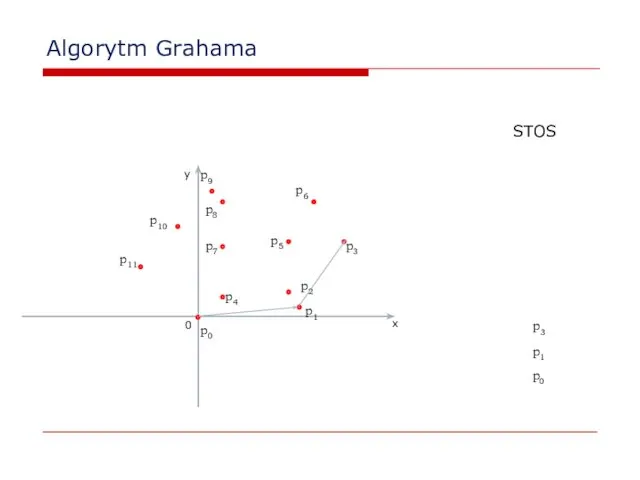
- 24. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p2 p3 p4 p5 p6
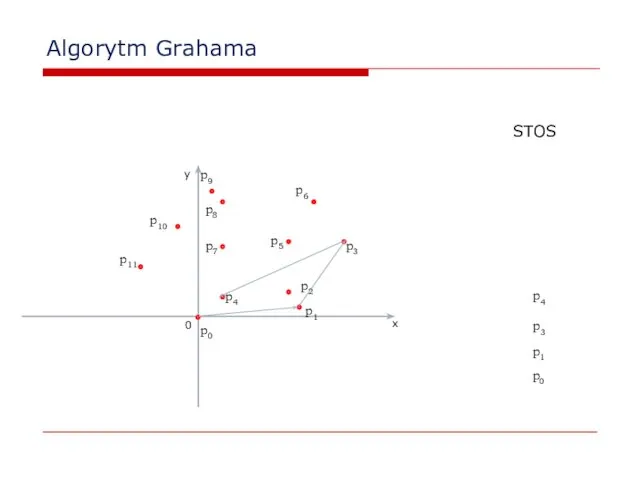
- 25. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
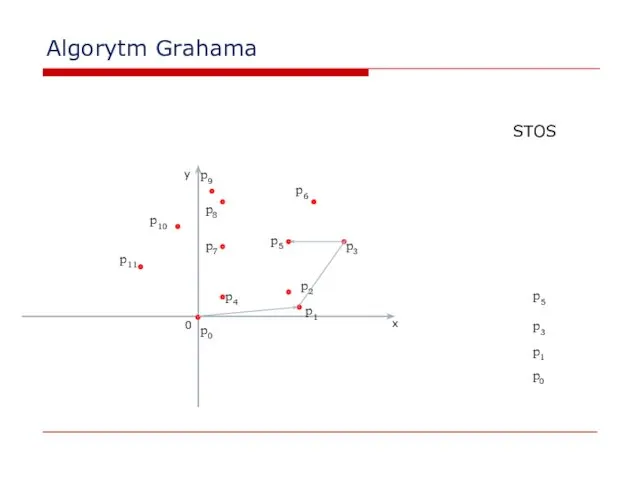
- 26. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
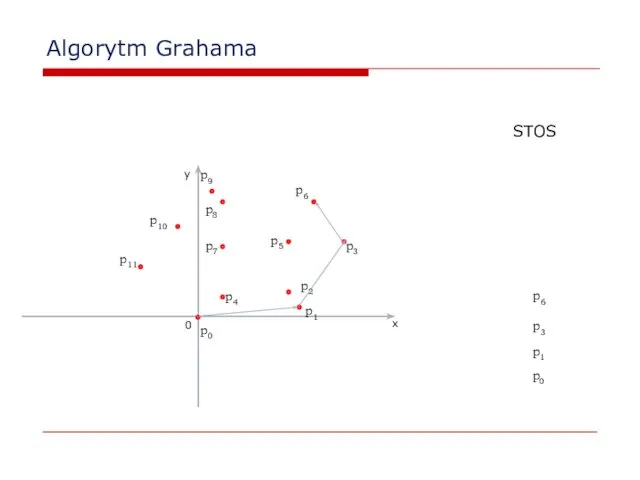
- 27. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
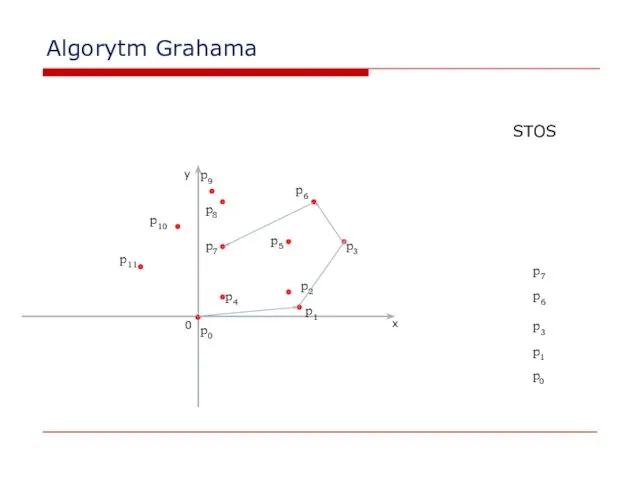
- 28. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
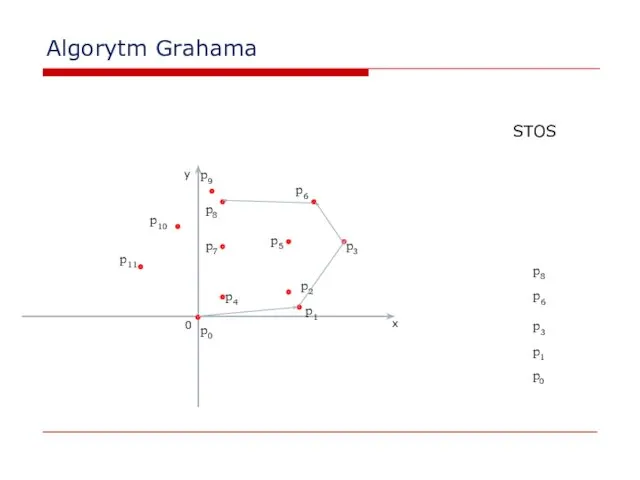
- 29. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
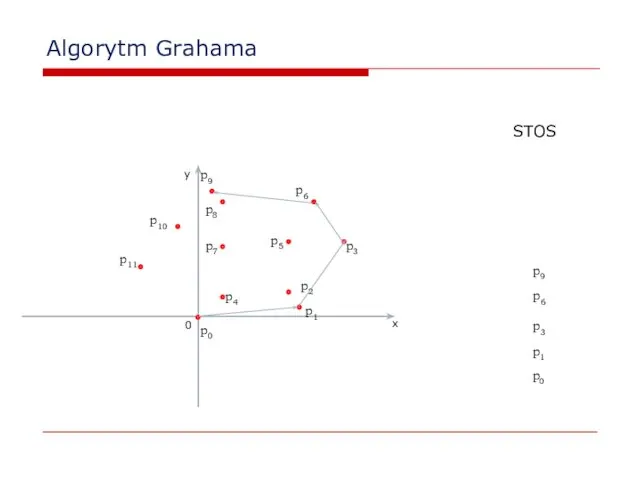
- 30. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
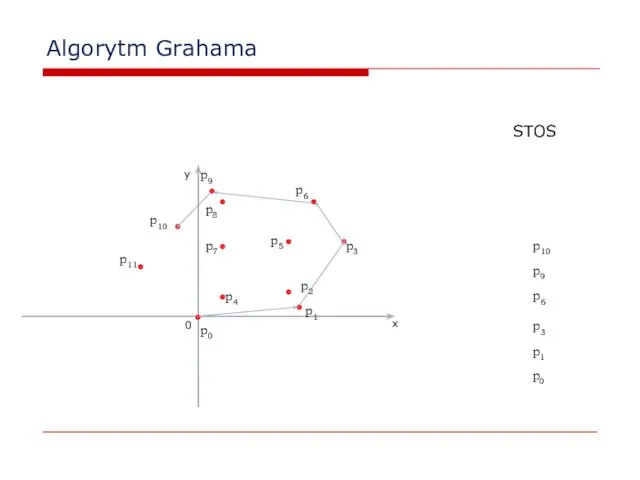
- 31. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
- 32. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
- 33. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
- 34. Algorytm Grahama 0 x y p2 p0 p1 STOS p0 p1 p3 p3 p4 p5 p6
- 35. Algorytm Grahama Niech p0 będzie punktem o najmniejszej współrzędnej y, jeśli takich jest kilka, bierzemy ten
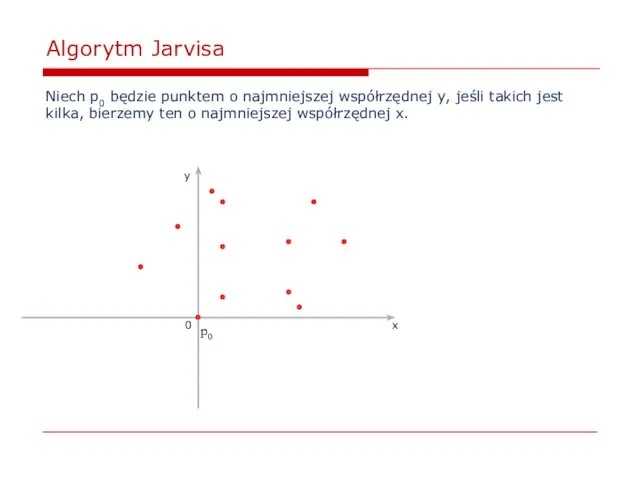
- 36. Algorytm Jarvisa Niech p0 będzie punktem o najmniejszej współrzędnej y, jeśli takich jest kilka, bierzemy ten
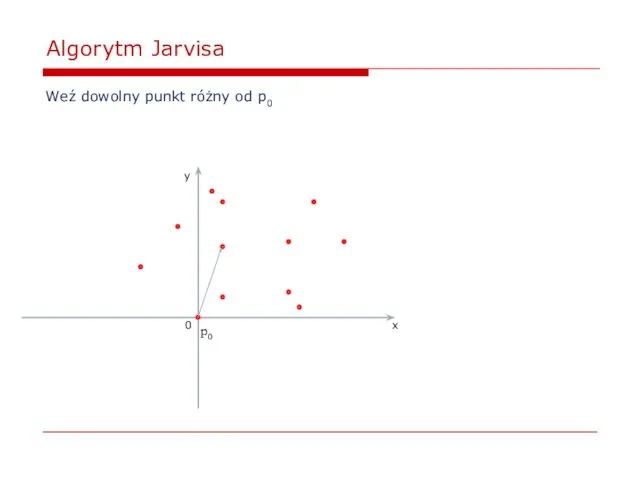
- 37. Algorytm Jarvisa Weź dowolny punkt różny od p0 0 x y p0
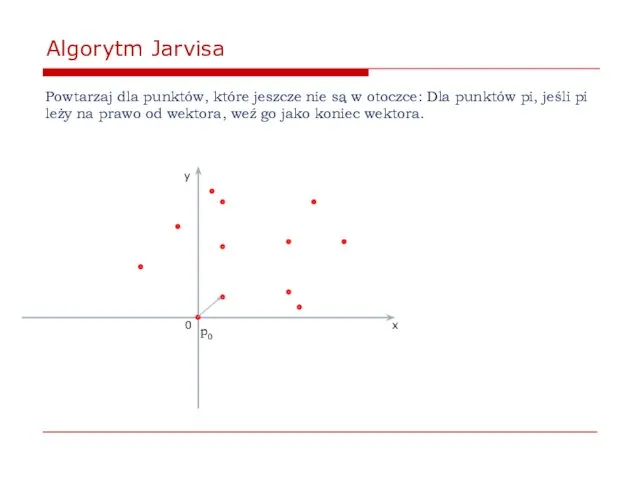
- 38. Algorytm Jarvisa Powtarzaj dla punktów, które jeszcze nie są w otoczce: Dla punktów pi, jeśli pi
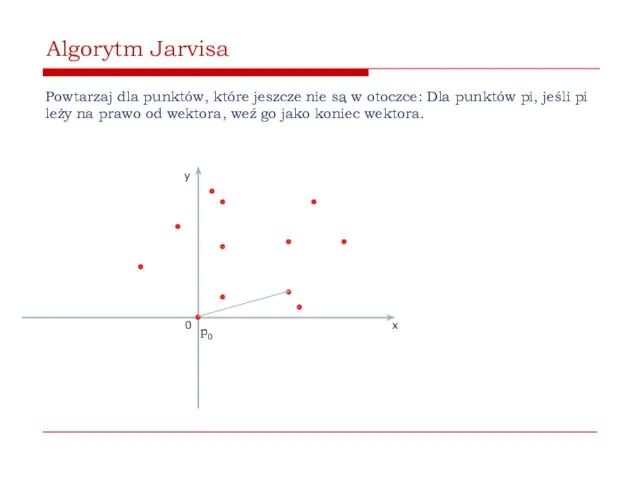
- 39. Algorytm Jarvisa Powtarzaj dla punktów, które jeszcze nie są w otoczce: Dla punktów pi, jeśli pi
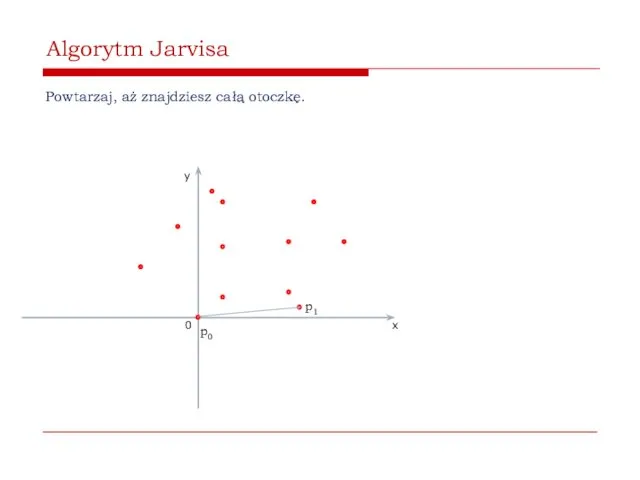
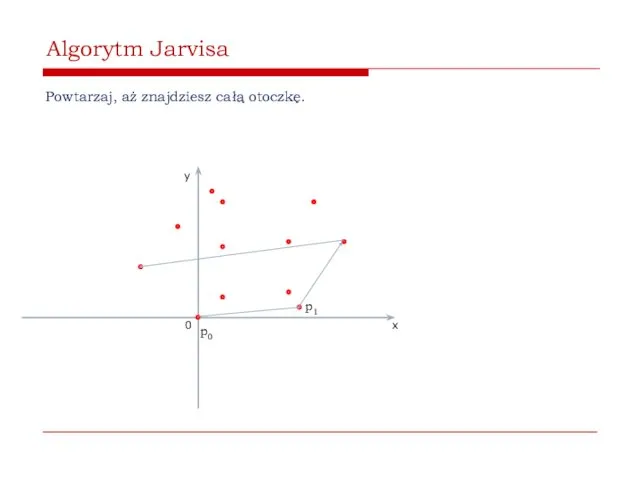
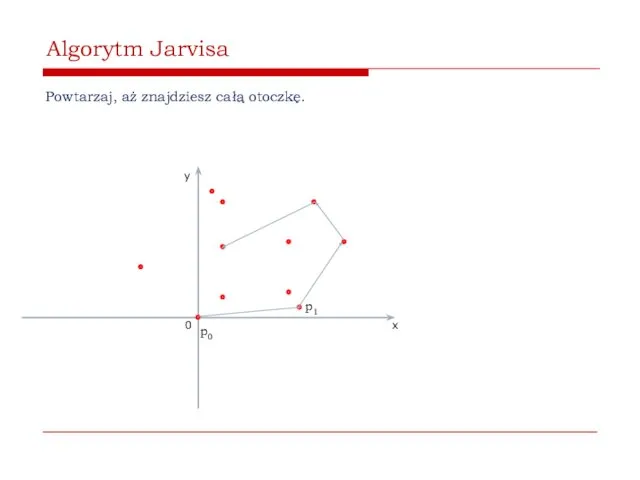
- 40. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
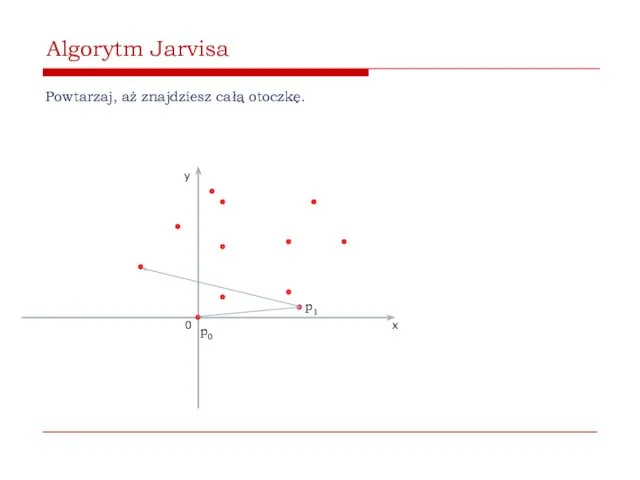
- 41. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
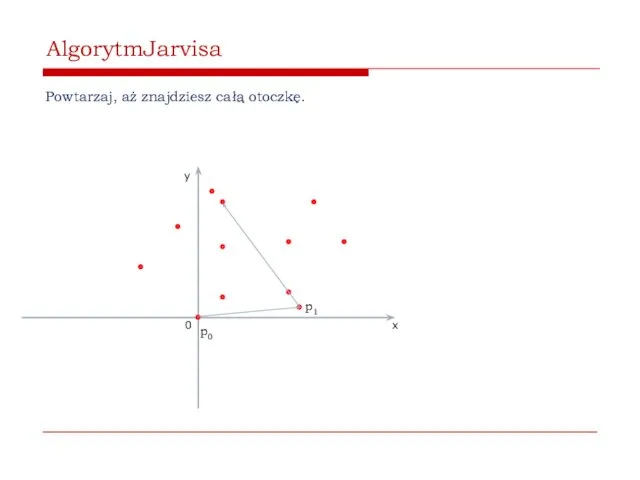
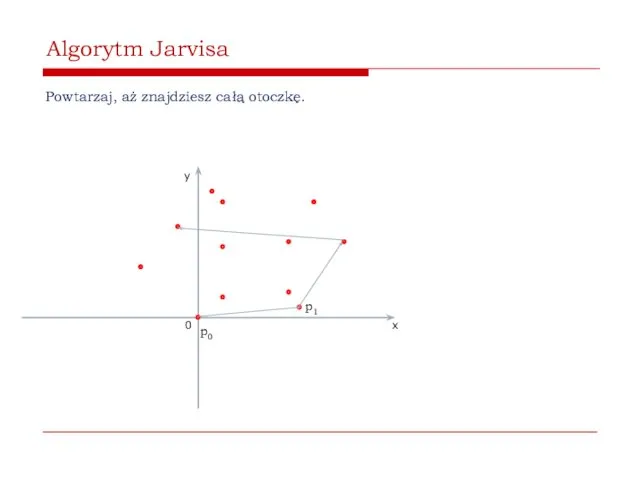
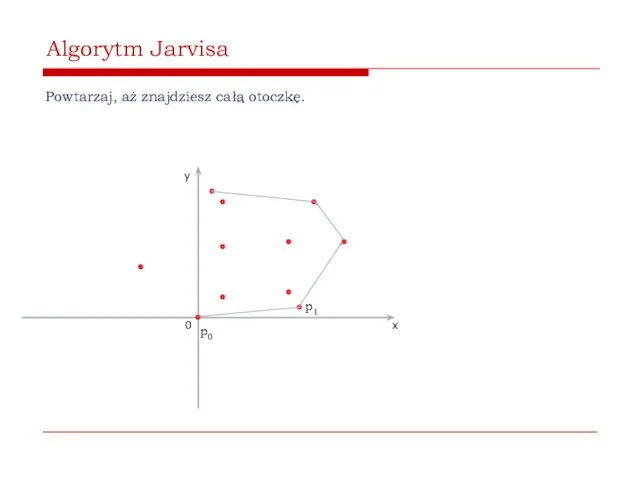
- 42. AlgorytmJarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
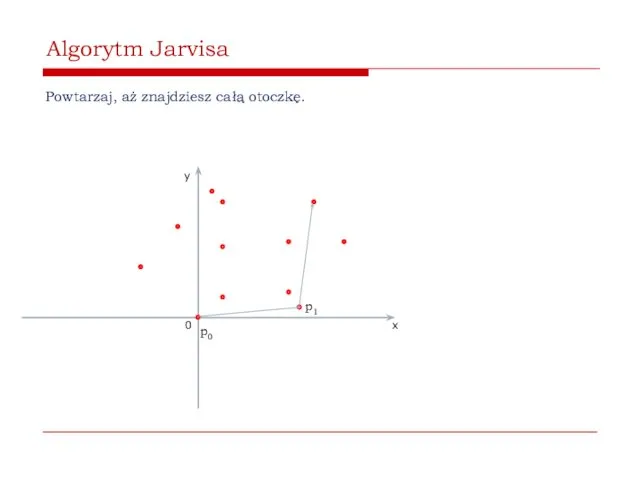
- 43. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
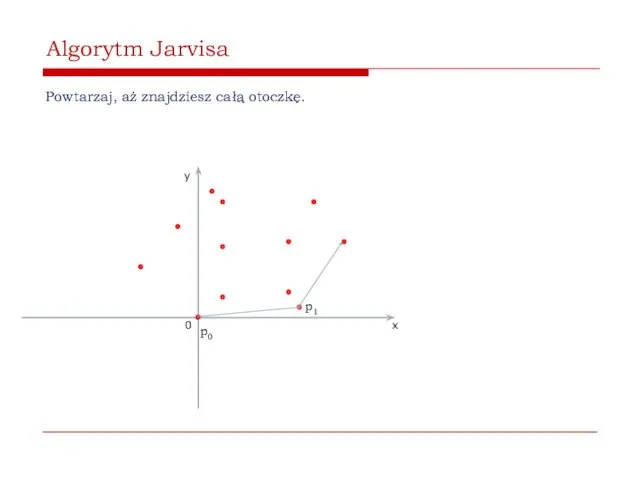
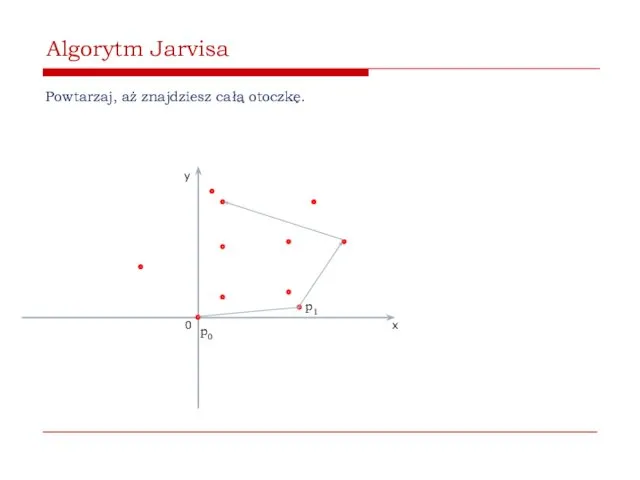
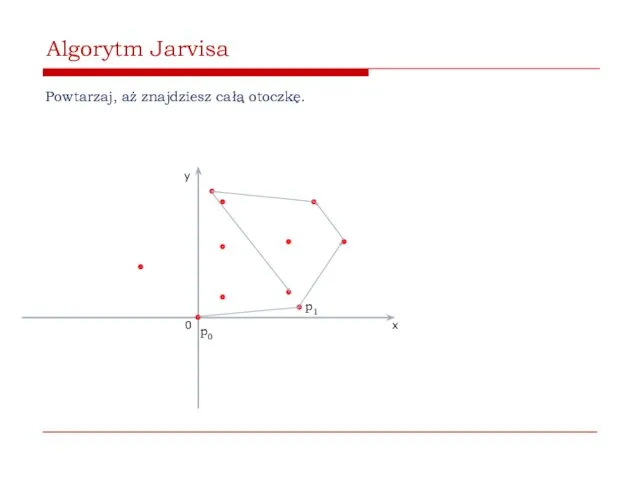
- 44. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
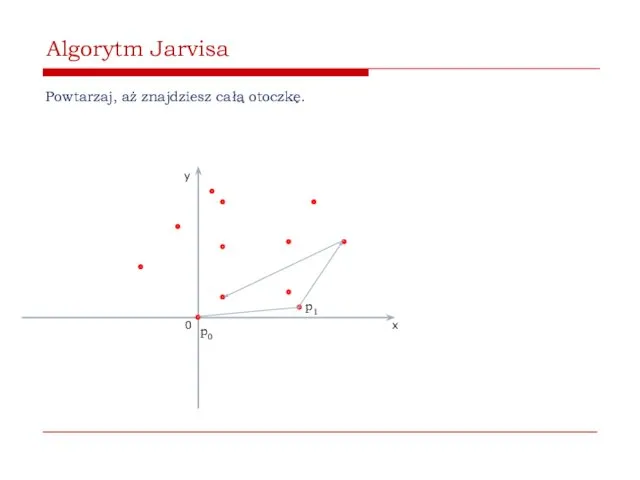
- 45. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
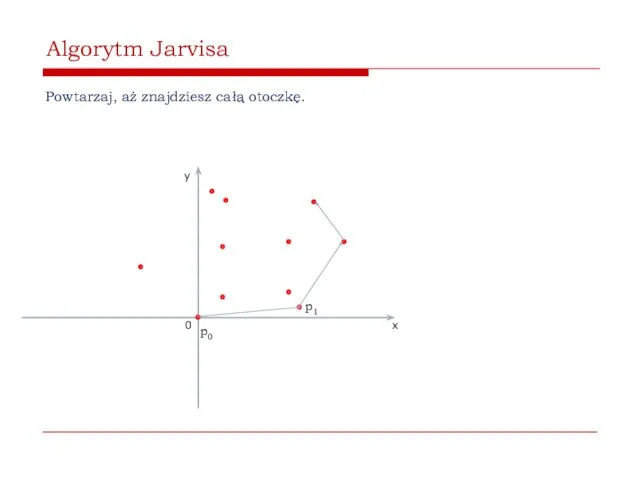
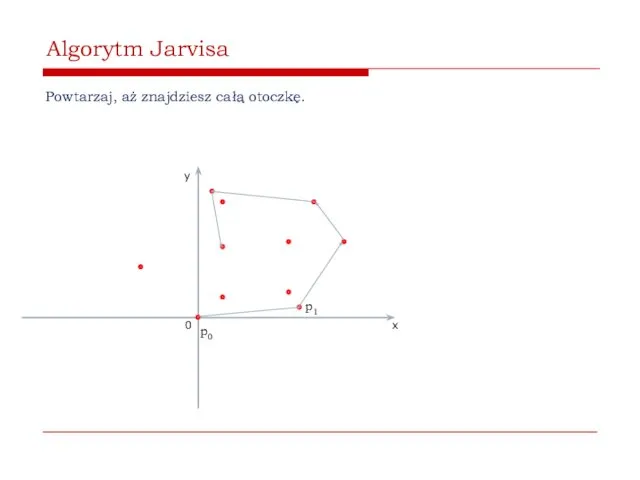
- 46. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
- 47. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
- 48. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
- 49. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
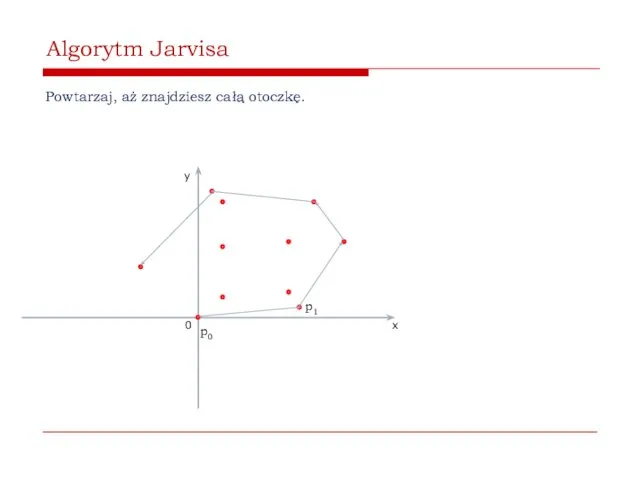
- 50. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
- 51. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
- 52. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
- 53. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
- 54. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. 0 x y p0 p1
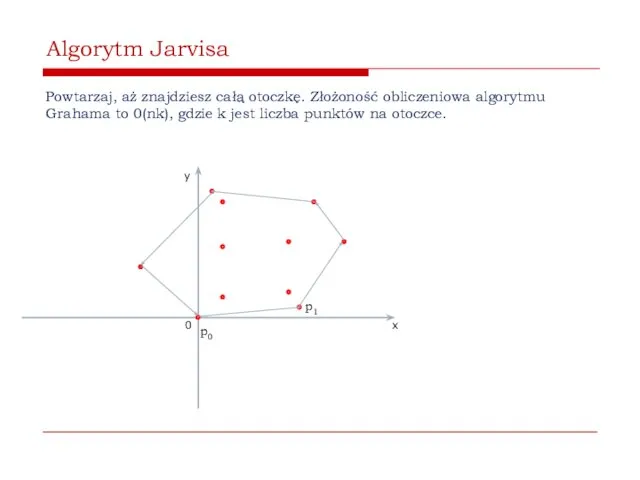
- 55. Algorytm Jarvisa Powtarzaj, aż znajdziesz całą otoczkę. Złożoność obliczeniowa algorytmu Grahama to 0(nk), gdzie k jest
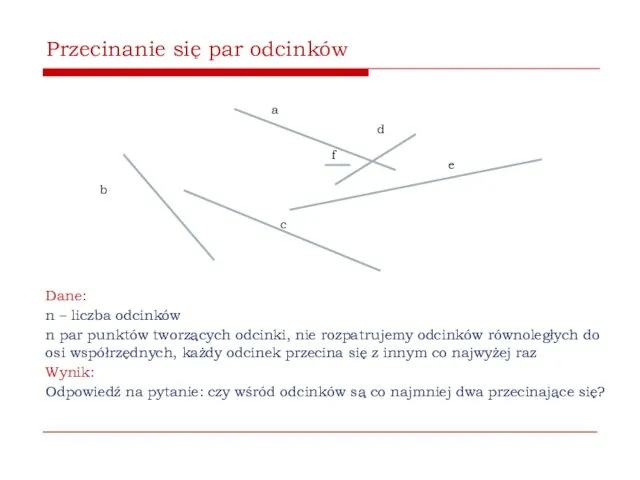
- 56. Dane: n – liczba odcinków n par punktów tworzących odcinki, nie rozpatrujemy odcinków równoległych do osi
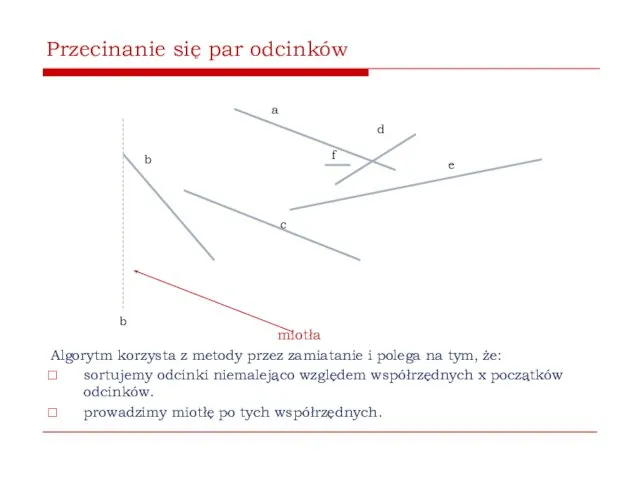
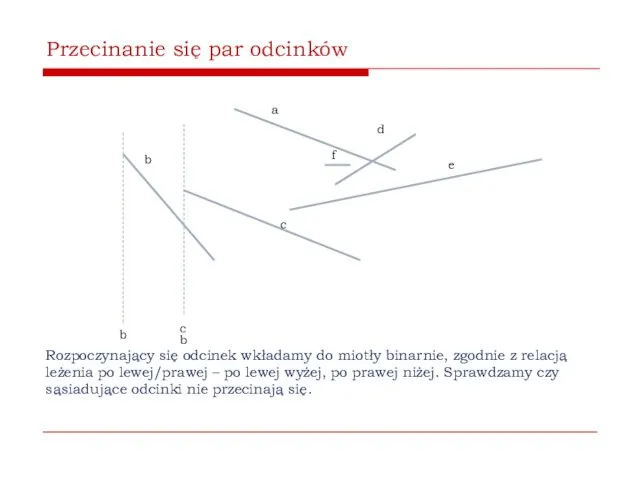
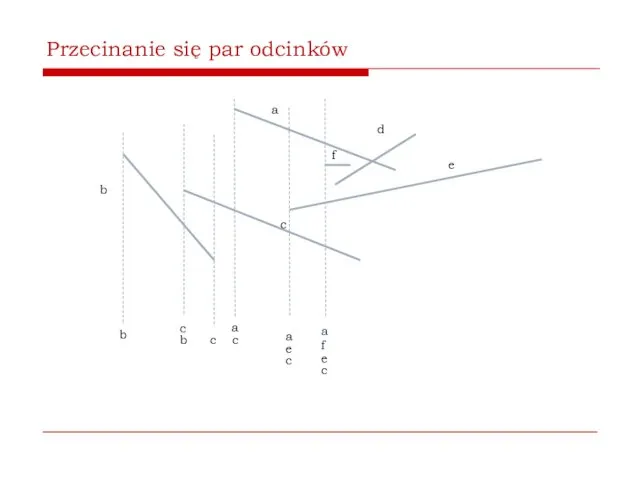
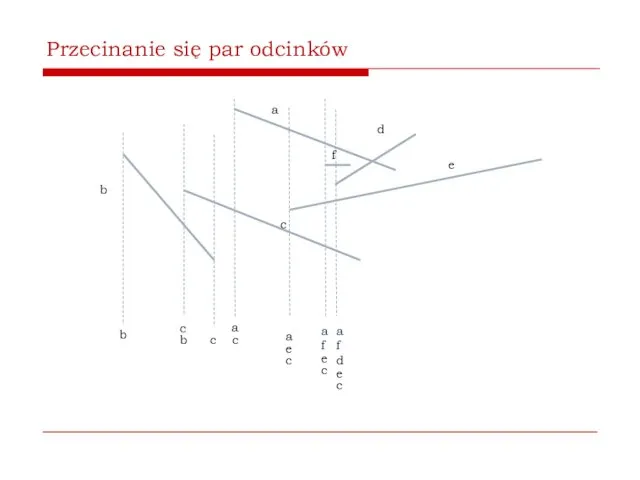
- 57. Przecinanie się par odcinków b a c d e b miotła Algorytm korzysta z metody przez
- 58. Przecinanie się par odcinków b a c d e b c b Rozpoczynający się odcinek wkładamy
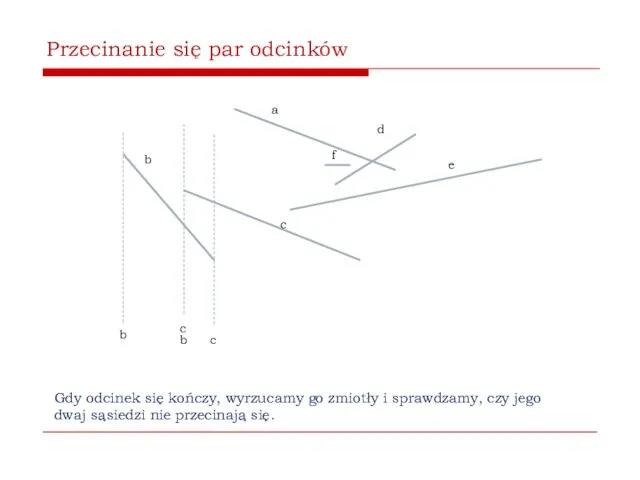
- 59. Przecinanie się par odcinków b a c d e b c b c Gdy odcinek się
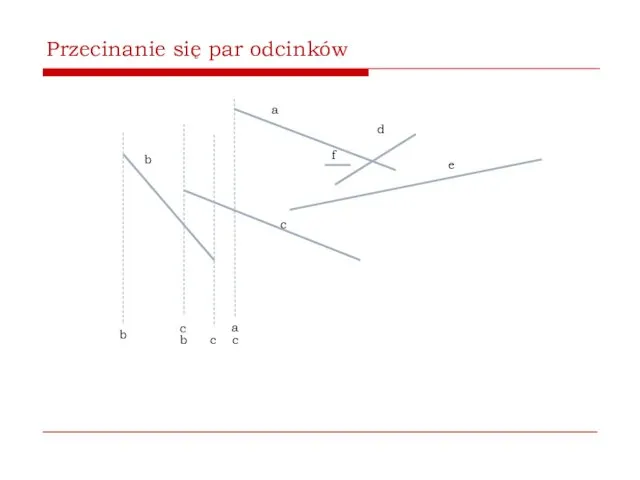
- 60. Przecinanie się par odcinków b a c d e b c b c a c f
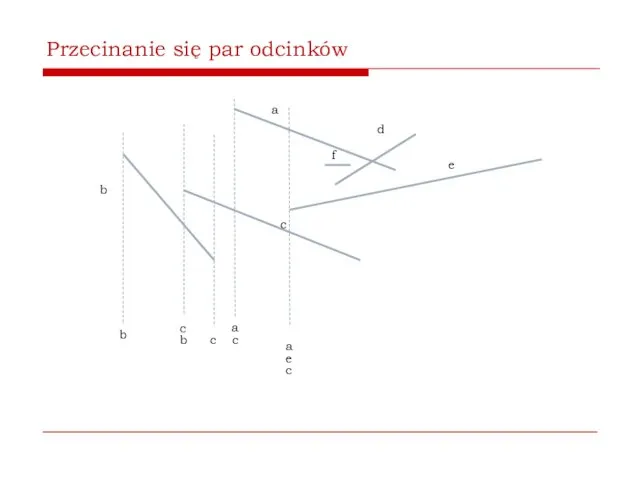
- 61. Przecinanie się par odcinków b a c d e b c b c a e c
- 62. Przecinanie się par odcinków b a c d e b c b c a e c
- 63. Przecinanie się par odcinków b a c d e b c b c a e c
- 65. Скачать презентацию
















 Таблиця множення числа 6
Таблиця множення числа 6 Эта многоликая парабола
Эта многоликая парабола Весёлые клоуны. «Интерактивная мозаика»
Весёлые клоуны. «Интерактивная мозаика» Логарифмы. Их применение в ТОРАТ. Мансуров
Логарифмы. Их применение в ТОРАТ. Мансуров Решение задач с помощью уравнений (6 класс)
Решение задач с помощью уравнений (6 класс) Координатная плоскость. Рене Декарт
Координатная плоскость. Рене Декарт Краткий обзор методов статистического анализа количественных переменных
Краткий обзор методов статистического анализа количественных переменных Интерполирование функций. Интерполяционный многочлен Лагранжа
Интерполирование функций. Интерполяционный многочлен Лагранжа Формулы пути
Формулы пути Призма. Элементы призмы. Площадь полной поверхности
Призма. Элементы призмы. Площадь полной поверхности Искусственный интеллект – наука и технология создания интеллектуальных машин
Искусственный интеллект – наука и технология создания интеллектуальных машин Работа по теме « Средняя линия трапеции» Ученика 9-2 класса Школы №593 Андреева Георгия Преподаватель : Петрова Наталья Васильевн
Работа по теме « Средняя линия трапеции» Ученика 9-2 класса Школы №593 Андреева Георгия Преподаватель : Петрова Наталья Васильевн Модуль Финские технологии в обучении математике
Модуль Финские технологии в обучении математике Нам радостно, нам весело! Смеемся мы с утра. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Головки
Нам радостно, нам весело! Смеемся мы с утра. Но вот пришло мгновенье, Серьезным быть пора. Глазки прикрыли, ручки сложили, Головки  Работа учителя лицея №58 Красковой И.В.
Работа учителя лицея №58 Красковой И.В.  Вписанные и центральные углы
Вписанные и центральные углы Оси симметрии фигуры
Оси симметрии фигуры Презентация на тему Аукцион «Продажа имения старой графини» ( математическая игра для 10-11 классов)
Презентация на тему Аукцион «Продажа имения старой графини» ( математическая игра для 10-11 классов) Формула Тейлора
Формула Тейлора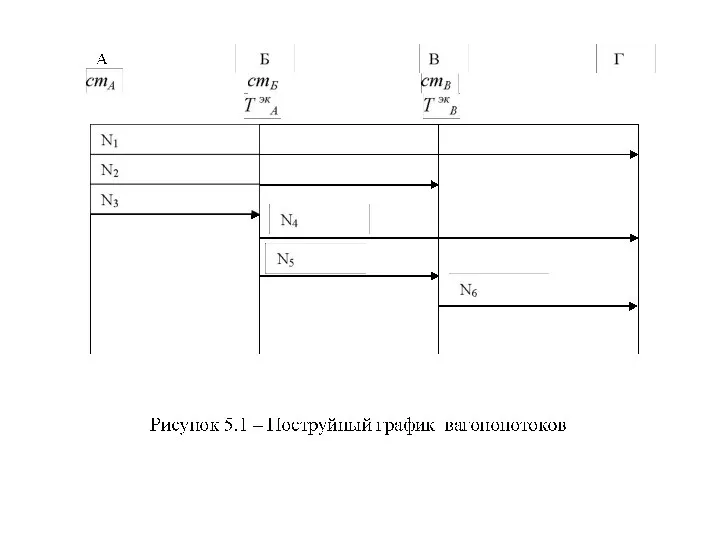 Классический способ расчета ПФ одногруппных сквозных поездов. (Тема 5)
Классический способ расчета ПФ одногруппных сквозных поездов. (Тема 5) Умножение и деление.Задачи
Умножение и деление.Задачи Образование чисел второго десятка Подготовила учитель начальных классов Чернышова Светлана Олеговна
Образование чисел второго десятка Подготовила учитель начальных классов Чернышова Светлана Олеговна  Статистика населения
Статистика населения Вписанная и описанная окружности
Вписанная и описанная окружности Признак равенства прямоугольных треугольников (по гипотенузе и катету)
Признак равенства прямоугольных треугольников (по гипотенузе и катету) Решение линейных уравнений с параметром и модулем
Решение линейных уравнений с параметром и модулем Блочная система обучения математике
Блочная система обучения математике Презентация на тему Многочлен и его стандартный вид
Презентация на тему Многочлен и его стандартный вид