Содержание
- 2. Если существует предел отношения при по любому закону, то этот предел называется производной функции f(z) в
- 3. Требование существования предела отношения и его независимость от закона стремления к нулю приращения переменной, накладывает на
- 4. Пусть тогда где
- 5. Тогда Если функция дифференцируема в точке z, то этот предел существует и не зависит от закона
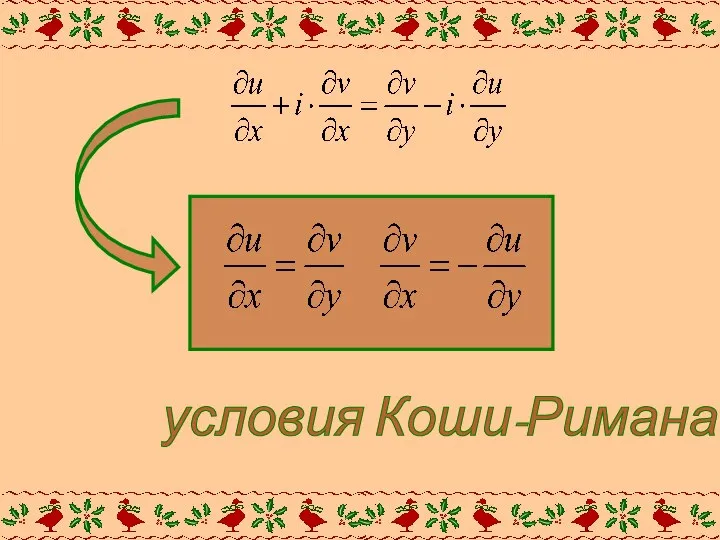
- 6. Если Δz = iΔy, то есть точка z+Δz приближается к точке z по прямой, параллельной оси
- 7. условия Коши-Римана
- 8. Это необходимое условие дифференцируемости ФКП. Оно должно выполнятся в любой точке, в которой функция f(z) дифференцируема.
- 9. Точки плоскости z, в которых функция f(z) аналитична, называются правильными точками этой функции. Точки плоскости z,
- 10. ПРИМЕРЫ. 1 Выяснить, являются ли данные функции аналитичными: 2 3
- 11. 1 Условия Коши-Римана выполняются во всех точках плоскости, следовательно функция является аналитичной на всей плоскости.
- 12. 2 Условия Коши-Римана выполняются во всех точках плоскости, следовательно функция является аналитичной на всей плоскости.
- 14. Скачать презентацию










 Пропорциональность величин. Урок 132
Пропорциональность величин. Урок 132 Измерения. Прямое измерение. Косвенное измерение
Измерения. Прямое измерение. Косвенное измерение Создание геометрических моделей для показа построения сечений геометрических фигур
Создание геометрических моделей для показа построения сечений геометрических фигур Тренажёр. Счёт с переходом через 10. (2 класс)
Тренажёр. Счёт с переходом через 10. (2 класс) Площадь треугольника
Площадь треугольника Книга из фетра Счет до 10
Книга из фетра Счет до 10 Переменная. Имя величины
Переменная. Имя величины Алгебраические дроби. Основное свойство алгебраической дроби. 8 класс
Алгебраические дроби. Основное свойство алгебраической дроби. 8 класс Теория систем. Система. Классификация систем. (Тема 3)
Теория систем. Система. Классификация систем. (Тема 3) Невский проспект Санкт-Петербурга в цифрах. Публичная библиотека в Санкт-Петербурге (часть 6)
Невский проспект Санкт-Петербурга в цифрах. Публичная библиотека в Санкт-Петербурге (часть 6) Лингвистика в математике
Лингвистика в математике Задачи городского тура олимпиады
Задачи городского тура олимпиады Сложность вычислений
Сложность вычислений Формула перехода от одного основания логарифма к другому
Формула перехода от одного основания логарифма к другому Детерминационный, факторный, кластерный анализ
Детерминационный, факторный, кластерный анализ Математическая игра «Колумбово яйцо»
Математическая игра «Колумбово яйцо» Цена. Количество. Стоимость
Цена. Количество. Стоимость Формирование смысла сложения и вычитания на примере УМК Гармония Н.Б. Истомина
Формирование смысла сложения и вычитания на примере УМК Гармония Н.Б. Истомина Жазықтықтар арасындағы бұрыш
Жазықтықтар арасындағы бұрыш Десятичные дроби
Десятичные дроби Четырехугольники. Параллелограмм
Четырехугольники. Параллелограмм Формулы приведения
Формулы приведения Средняя линия
Средняя линия Четные и нечётные функции
Четные и нечётные функции Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Правильные многоугольники
Правильные многоугольники Ике турының параллельлек билгеләре
Ике турының параллельлек билгеләре Предмет статистической науки
Предмет статистической науки